CNN卷积层和pooling层的前向传播和反向传播
title: CNN卷积层和pooling层的前向传播和反向传播
tags: CNN,反向传播,前向传播
grammar_abbr: true
grammar_table: true
grammar_defList: true
grammar_emoji: true
grammar_footnote: true
grammar_ins: true
grammar_mark: true
grammar_sub: true
grammar_sup: true
grammar_checkbox: true
grammar_mathjax: true
grammar_flow: true
grammar_sequence: true
grammar_plot: true
grammar_code: true
grammar_highlight: true
grammar_html: true
grammar_linkify: true
grammar_typographer: true
grammar_video: true
grammar_audio: true
grammar_attachment: true
grammar_mermaid: true
grammar_classy: true
grammar_cjkEmphasis: true
grammar_cjkRuby: true
grammar_center: true
grammar_align: true
grammar_tableExtra: true
本文只包含CNN的前向传播和反向传播,主要是卷积层和pool层的前向传播和反向传播,一些卷积网络的基础知识不涉及
符号表示
如果 l l l层是卷积层:
p [ l ] p^{[l]} p[l]: padding
s [ l ] s^{[l]} s[l]: stride
n c [ l ] n_c^{[l]} nc[l] : number of filters
fliter size: k 1 [ l ] × k 2 [ l ] × n c [ l − 1 ] k_1^{[l]} \times k_2^{[l]}\times n_c^{[l-1]} k1[l]×k2[l]×nc[l−1]
Weight: W [ l ] W^{[l]} W[l] size is k 1 [ l ] × k 2 [ l ] × n c l − 1 × n c l k_1^{[l]} \times k_2^{[l]} \times n_c^{l - 1} \times n_c^{l} k1[l]×k2[l]×ncl−1×ncl
bais: b [ l ] b^{[l]} b[l] size is n c [ l ] n_{c}^{[l]} nc[l]
liner: z [ l ] z^{[l]} z[l],size is n h [ l ] × n w [ l ] × n c [ l ] n_h^{[l]} \times n_w^{[l]} \times n_c^{[l ]} nh[l]×nw[l]×nc[l]
Activations: a [ l ] a^{[l]} a[l] size is n h [ l ] × n w [ l ] × n c [ l ] n_h^{[l]} \times n_w^{[l]} \times n_c^{[l ]} nh[l]×nw[l]×nc[l]
input: a [ l − 1 ] a^{[l-1]} a[l−1] size is n h [ l − 1 ] × n w [ l − 1 ] × n c [ l − 1 ] n_h^{[l-1]} \times n_w^{[l-1]} \times n_c^{[l - 1]} nh[l−1]×nw[l−1]×nc[l−1]
output: a [ l ] a^{[l]} a[l] size is n h [ l ] × n w [ l ] × n c [ l ] n_h^{[l]} \times n_w^{[l]} \times n_c^{[l ]} nh[l]×nw[l]×nc[l]
n h [ l ] n_h^{[l]} nh[l]和 n h [ l − 1 ] n_h^{[l-1]} nh[l−1]两者满足:
n h [ l ] ( s [ l ] − 1 ) + f 1 [ l ] ⩽ n h [ l − 1 ] + 2 p n_h^{[l]}({s^{[l]}} - 1) + {f_1^{[l]}} \leqslant n_h^{[l - 1]} + 2p nh[l](s[l]−1)+f1[l]⩽nh[l−1]+2p
n h [ l ] = ⌊ n h [ l − 1 ] + 2 p − k 1 [ l ] s + 1 ⌋ n_h^{[l]} = \left\lfloor {\frac{{n_h^{[l - 1]} + 2p - {k_1^{[l]}}}}{s} + 1} \right\rfloor nh[l]=⌊snh[l−1]+2p−k1[l]+1⌋
符号 ⌊ x ⌋ \left\lfloor {x} \right\rfloor ⌊x⌋表示向下取整, n w [ l ] n_w^{[l]} nw[l]和 n w [ l − 1 ] n_w^{[l-1]} nw[l−1]两者关系同上
[外链图片转存失败(img-S6uM1cnE-1567131135563)(https://www.github.com/callMeBigKing/story_writer_note/raw/master/小书匠/1535388857043.png)]
Cross-correlation与Convolution
很多文章或者博客中把Cross-correlation(互相关)和Convolution(卷积)都叫卷积,把互相关叫做翻转的卷积,在我个人的理解里面两者是有区别的,本文将其用两种表达式分开表示,不引入翻转180度。
Cross-correlation
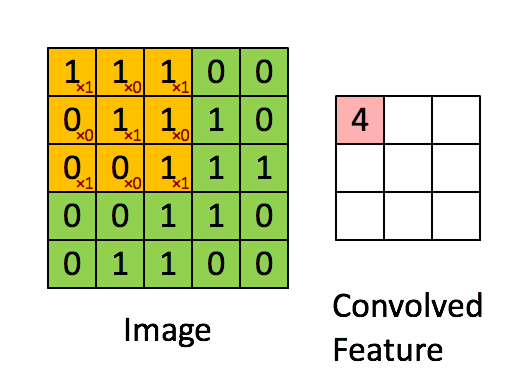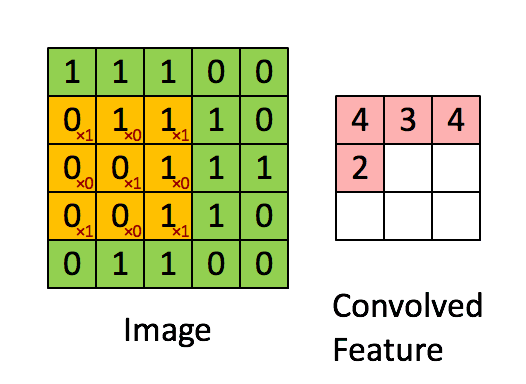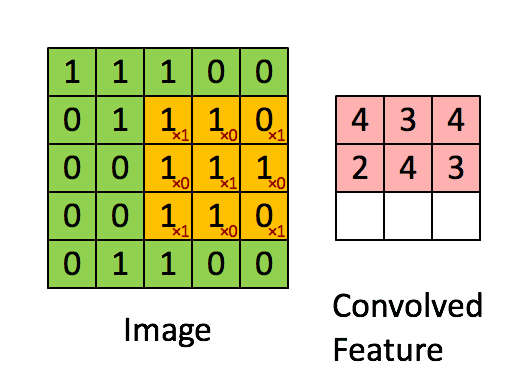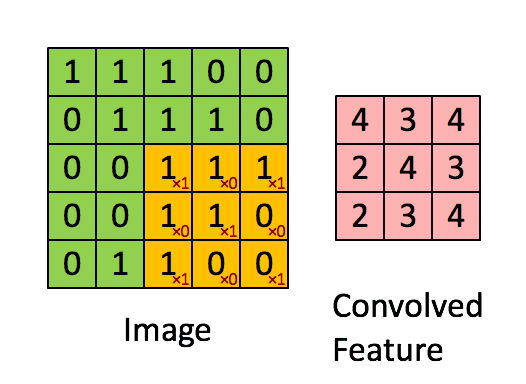
对于大小为 h × w h \times w h×w图像 I I I和 大小为 ( k 1 × k 2 ) (k_1 \times k_2) (k1×k2)kernel K K K,定义其Cross-correlation:
( I ⊗ K ) i j = ∑ m = 0 k 1 − 1 ∑ n = 0 k 2 I ( i + m , j + n ) K ( m , n ) {(I \otimes K)_{ij}} = \sum\limits_{m = 0}^{{k_1} - 1} {\sum\limits_{n = 0}^{{k_2}} {I(i + m,j + n)} } K(m,n) (I⊗K)ij=m=0∑k1−1n=0∑k2I(i+m,j+n)K(m,n)
其中
0 ⩽ i ⩽ h − k 1 + 1 0 \leqslant i \leqslant h - {k_1} + 1 0⩽i⩽h−k1+1
0 ⩽ j ⩽ w − k 2 + 1 0 \leqslant j \leqslant w - {k_2} + 1 0⩽j⩽w−k2+1
注意这里的使用的符号和 i i i的范围,不考虑padding的话Cross-correlation会产生一个较小的矩阵
Convolution
首先回顾一下连续函数的卷积和一维数列的卷积分别如下,卷积满足交换律:
h ( t ) = ∫ − ∞ ∞ f ( τ ) g ( t − τ ) d τ h(t) = \int_{ - \infty }^\infty {f(\tau )g(t - \tau )d\tau } h(t)=∫−∞∞f(τ)g(t−τ)dτ
c ( n ) = ∑ i = − ∞ ∞ a ( i ) b ( n − i ) d i c(n) = \sum\limits_{i = - \infty }^\infty {a(i)b(n - i)di} c(n)=i=−∞∑∞a(i)b(n−i)di
对于大小为 h × w h \times w h×w图像 I I I和大小为 ( k 1 × k 2 ) (k_1 \times k_2) (k1×k2)kernel K K K,convolution为 :
( I ∗ K ) i j = ( K ∗ I ) i j = ∑ m = 0 k 1 − 1 ∑ n = 0 k 2 − 1 I ( i − m , j − n ) k ( m , n ) {(I * K)_{ij}} = {(K * I)_{ij}} = \sum\limits_{m = 0}^{{k_1} - 1} {\sum\limits_{n = 0}^{{k_2} - 1} {I(i - m,j - n)k(m,n)} } (I∗K)ij=(K∗I)ij=m=0∑k1−1n=0∑k2−1I(i−m,j−n)k(m,n)
KaTeX parse error: Expected 'EOF', got '\eqalign' at position 1: \̲e̲q̲a̲l̲i̲g̲n̲{ & 0 \leqsla…
注意:这里的Convolution和前面的cross-correlation是不同的:
- i , j i,j i,j范围变大了,卷积产生的矩阵size变大了
- 这里出现了很多 I ( − x , − y ) I(-x,-y) I(−x,−y),这些负数索引可以理解成padding
- 这里的卷积核会翻转180度
具体过程如下图所示
[外链图片转存失败(img-fpdG5ZPq-1567131135566)(https://hosbimkimg.oss-cn-beijing.aliyuncs.com/pic/卷积示意图new.svg “卷积示意图”)]
如果把卷积的padding项扔掉那么就变成下图这样,此时Convolution和Cross-correlation相隔的就是一个180度的翻转,如下图所示
卷积核旋转180度
参考自卷积核翻转方法
翻转卷积核有三种方法,具体步骤移步卷积核翻转方法
-
围绕卷积核中心旋转180度 (奇数行列好使)
-
沿着两条对角线翻转两次
-
同时翻转行和列 (偶数行列好使)
前向传播
卷积层
前向传播:计算 z [ l ] z^{[l]} z[l]和 a [ l ] a^{[l]} a[l]
输入: a [ l − 1 ] a^{[l-1]} a[l−1] size is n h [ l − 1 ] × n w [ l − 1 ] × n c [ l − 1 ] n_h^{[l-1]} \times n_w^{[l-1]} \times n_c^{[l - 1]} nh[l−1]×nw[l−1]×nc[l−1]
输出: a [ l ] a^{[l]} a[l]
为了方便后续的反向传播的方便,只讨论 l l l层的参数,把部分上标 [ l ] [l] [l]去掉,同时另 n c [ l ] = n c [ l − 1 ] = 1 n_c^{[l]}=n_c^{[l-1]}=1 nc[l]=nc[l−1]=1,前向传播公式如下:
KaTeX parse error: Expected 'EOF', got '\eqalign' at position 1: \̲e̲q̲a̲l̲i̲g̲n̲{ {z^l}(i,j) …
虑通道和padding的前向传播
pooling层
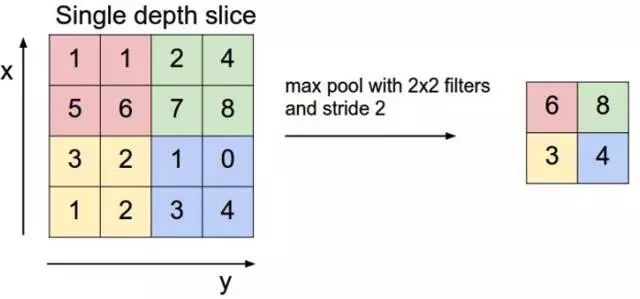
pooling层进行下采样,maxpool可以表示为:
a l ( i , j ) = max 0 ⩽ m ⩽ k 1 − 1 , 0 ⩽ n ⩽ k 2 − 1 ( a l − 1 ( i * k 1 + m , j * k 2 + n ) ) {a^l}(i,j) = \mathop {\max }\limits_{0 \leqslant m \leqslant {k_1} - 1,0 \leqslant n \leqslant {k_2} - 1} ({a^{l - 1}}(i{\text{*}}{k_1} + m,j{\text{*}}{k_2} + n)) al(i,j)=0⩽m⩽k1−1,0⩽n⩽k2−1max(al−1(i*k1+m,j*k2+n))
avepool可以表示为:
a l ( i , j ) = 1 k 1 × k 2 ∑ m = 0 k 1 − 1 ∑ n = 0 k 2 − 1 a l − 1 ( i * k 1 + m , j * k 2 + n ) {a^l}(i,j) = \frac{1}{{{k_1} \times {k_2}}}\sum\limits_{m = 0}^{{k_1} - 1} {\sum\limits_{n = 0}^{{k_2} - 1} {{a^{l - 1}}(i{\text{*}}{k_1} + m,j{\text{*}}{k_2} + n)} } al(i,j)=k1×k21m=0∑k1−1n=0∑k2−1al−1(i*k1+m,j*k2+n)
反向传播
卷积层的反向传播
1. 已知 ∂ E ∂ z l \frac{{\partial E}}{{\partial {z^l}}} ∂zl∂E求 ∂ E ∂ w l \frac{{\partial E}}{{\partial {w^l}}} ∂wl∂E
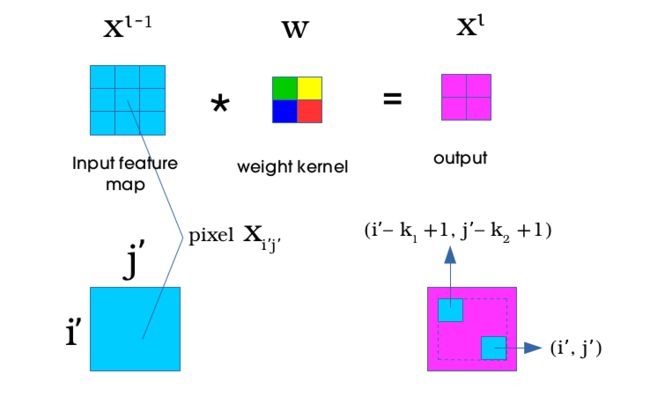
由上图可知 W W W对每一个元素都有贡献,(偷来的图,用的符号不一致),使用链式法则有:
∂ E ∂ w m ′ , n ′ l = ∑ i = 0 n h l − 1 ∑ j = 0 n w l − 1 ∂ E ∂ z i , j l ∂ z i , j l ∂ w m ′ , n ′ l \frac{{\partial E}}{{\partial w_{m',n'}^l}} = \sum\limits_{i = 0}^{n_h^l - 1} {\sum\limits_{j = 0}^{n_w^l - 1} {\frac{{\partial E}}{{\partial z_{i,j}^l}}} } \frac{{\partial z_{i,j}^l}}{{\partial w_{m',n'}^l}} ∂wm′,n′l∂E=i=0∑nhl−1j=0∑nwl−1∂zi,jl∂E∂wm′,n′l∂zi,jl
∂ z i , j l ∂ w m ′ , n ′ l = ∂ ( ∑ m = 0 k 1 − 1 ∑ n = 0 k 2 − 1 a i + m , j + n l − 1 × w m , n + b ) ∂ w m ′ , n ′ l = a i + m ′ , j + n ′ l − 1 \frac{{\partial z_{i,j}^l}}{{\partial w_{m',n'}^l}} = \frac{{\partial \left( {\sum\limits_{m = 0}^{{k_1} - 1} {\sum\limits_{n = 0}^{{k_2} - 1} {a_{i + m,j + n}^{l - 1} \times } {w_{m,n}}} + b} \right)}}{{\partial w_{m',n'}^l}} = a_{i + m',j + n'}^{l - 1} ∂wm′,n′l∂zi,jl=∂wm′,n′l∂(m=0∑k1−1n=0∑k2−1ai+m,j+nl−1×wm,n+b)=ai+m′,j+n′l−1
记 δ i , j l = ∂ E ∂ z i , j l \delta _{i,j}^l = \frac{{\partial E}}{{\partial z_{i,j}^l}} δi,jl=∂zi,jl∂E,有:
KaTeX parse error: Expected 'EOF', got '\eqalign' at position 1: \̲e̲q̲a̲l̲i̲g̲n̲{ \frac{{\par…
2. 根据 ∂ E ∂ z l \frac{{\partial E}}{{\partial {z^l}}} ∂zl∂E求 ∂ E ∂ z l − 1 \frac{{\partial E}}{{\partial {z^{l - 1}}}} ∂zl−1∂E
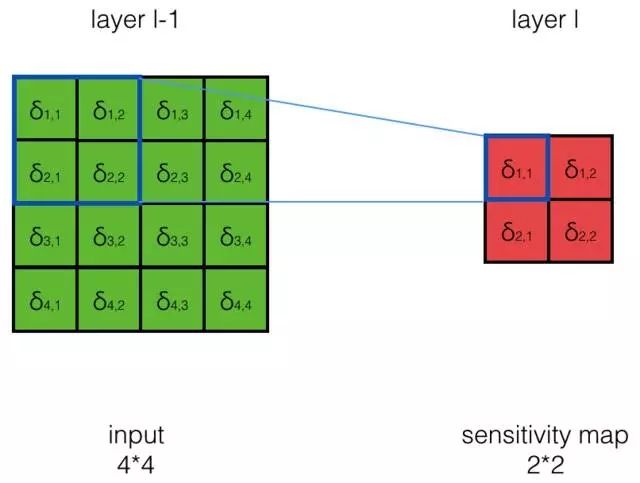
上图是偷来的图,把那边的 X l X^l Xl,当成 z l z^l zl理解,与 z i ′ , j ′ l − 1 z_{i',j'}^{l - 1} zi′,j′l−1
有关的 a i , j l − 1 a_{i,j}^{l - 1} ai,jl−1,索引是从 ( i ′ − k 1 + 1 , j ′ − k 2 + 1 ) (i' - {k_1} + 1,j' - {k_2} + 1) (i′−k1+1,j′−k2+1)到 ( i ′ , j ′ ) (i',j') (i′,j′)(出现负值或者是越界当成是padding),根据链式法则:
∂ E ∂ z i ′ , j ′ l − 1 = ∑ m = 0 k 1 − 1 ∑ n = 0 k 2 + 1 ∂ E ∂ z i ′ − m , j ′ − n l ∂ z i ′ − m , j ′ − n l ∂ z i ′ , j ′ l − 1 \frac{{\partial E}}{{\partial z_{i',j'}^{l - 1}}} = \sum\limits_{m = 0}^{{k_1} - 1} {\sum\limits_{n = 0}^{{k_2} + 1} {\frac{{\partial E}}{{\partial z_{i' - m,j' - n}^l}}\frac{{\partial z_{i' - m,j' - n}^l}}{{\partial z_{i',j'}^{l - 1}}}} } ∂zi′,j′l−1∂E=m=0∑k1−1n=0∑k2+1∂zi′−m,j′−nl∂E∂zi′,j′l−1∂zi′−m,j′−nl
将 ∂ z i ′ − m , j ′ − n l ∂ z i ′ , j ′ l − 1 \frac{{\partial z_{i' - m,j' - n}^l}}{{\partial z_{i',j'}^{l - 1}}} ∂zi′,j′l−1∂zi′−m,j′−nl展开有:
∂ z i ′ − m , j ′ − n l ∂ z i ′ , j ′ l − 1 = ∂ ∑ s = 0 k 1 − 1 ∑ t = 0 k 2 + 1 z i ′ − m + s , j ′ − n + t l − 1 w s , t l ∂ z i ′ , j ′ l − 1 = w m , n l \frac{{\partial z_{i' - m,j' - n}^l}}{{\partial z_{i',j'}^{l - 1}}} = \frac{{\partial \sum\limits_{s = 0}^{{k_1} - 1} {\sum\limits_{t = 0}^{{k_2} + 1} {z_{i' - m + s,j' - n + t}^{l - 1}w_{s,t}^l} } }}{{\partial z_{i',j'}^{l - 1}}} = w_{m,n}^l ∂zi′,j′l−1∂zi′−m,j′−nl=∂zi′,j′l−1∂s=0∑k1−1t=0∑k2+1zi′−m+s,j′−n+tl−1ws,tl=wm,nl
从而可以得到:
KaTeX parse error: Expected 'EOF', got '\eqalign' at position 1: \̲e̲q̲a̲l̲i̲g̲n̲{ \frac{{\par…
这里的 ∗ * ∗代表是卷积操作
pooling层的反向传播
pooling层的反向传播比较简,没有要训练的参数
maxpool,最大的那个为1其他的均为0:
KaTeX parse error: Expected 'EOF', got '\eqalign' at position 1: \̲e̲q̲a̲l̲i̲g̲n̲{ & \frac{{\p…
avepool,每个都是
∂ E ∂ a i ′ , j ′ l − 1 = 1 k 1 × k 2 \frac{{\partial E}}{{\partial a_{i',j'}^{l - 1}}} = \frac{1}{{{k_1} \times {k_2}}} ∂ai′,j′l−1∂E=k1×k21
附
考虑多个通道
用 z c [ l ] [ l ] z_{{c^{[l]}}}^{[l]} zc[l][l]表示 z [ l ] z^{[l]} z[l]的第 c [ l ] c^{[l]} c[l]个channel:
KaTeX parse error: Expected 'EOF', got '\eqalign' at position 1: \̲e̲q̲a̲l̲i̲g̲n̲{ & z_{{c^{[l…
其中, W c [ l − 1 ] , c [ l ] [ l ] {W_{{c^{[l - 1]}},{c^{[l]}}}^{[l]}} Wc[l−1],c[l][l]为 f [ l ] × f [ l ] f^{[l]} \times f^{[l]} f[l]×f[l]的卷积核 W c [ l − 1 ] , c [ l ] [ l ] = W [ l ] ( : , : , c [ l − 1 ] , c [ l ] ) {W_{{c^{[l - 1]}},{c^{[l]}}}^{[l]}}={{W^{[l]}}(:,:,{c^{[l - 1]}},{c^{[l]}})} Wc[l−1],c[l][l]=W[l](:,:,c[l−1],c[l])
a c [ l ] [ l ] = g ( z c [ l ] [ l ] ) a_{{c^{[l]}}}^{[l]} = g(z_{{c^{[l]}}}^{[l]}) ac[l][l]=g(zc[l][l])
g ( x ) g(x) g(x)为激活函数
考虑padding和stride情况下:
z c [ l ] [ l ] ( i , j ) = ∑ c [ l − 1 ] = 0 n c l − 1 − 1 ( ∑ m = 0 f [ l ] − 1 ∑ n = 0 f [ l ] − 1 a [ l − 1 ] ( i ∗ s + m − p , j ∗ s + n − p , c [ l − 1 ] ) × W [ l ] ( m , n , c [ l − 1 ] , c [ l ] ) ) + b c l [ l ] z_{{c^{[l]}}}^{[l]}(i,j) = \sum\limits_{{c^{[l - 1]}} = 0}^{n_c^{l - 1} - 1} {(\sum\limits_{m = 0}^{{f^{[l]}} - 1} {\sum\limits_{n = 0}^{{f^{[l]}} - 1} {{a^{[l-1]}}(i*s + m - p,j*s + n - p,{c^{[l - 1]}}) \times } {W^{[l]}}(m,n,{c^{[l - 1]}},{c^{[l]}})} )} + b_{{c^l}}^{[l]} zc[l][l](i,j)=c[l−1]=0∑ncl−1−1(m=0∑f[l]−1n=0∑f[l]−1a[l−1](i∗s+m−p,j∗s+n−p,c[l−1])×W[l](m,n,c[l−1],c[l]))+bcl[l]
a c [ l ] [ l ] = g ( z c [ l ] [ l ] ) a_{{c^{[l]}}}^{[l]} = g(z_{{c^{[l]}}}^{[l]}) ac[l][l]=g(zc[l][l])
a [ l ] a^{[l]} a[l]索引越界部分表示padding,其值为0