薄板样条函数(Thin plate splines)的讨论与分析

薄板样条函数(TPS)是一种很常见的插值方法。因为它一般都是基于2D插值，所以经常用在在图像配准中。在两张图像中找出N个匹配点，应用TPS可以将这N个点形变到对应位置，同时给出了整个空间的形变(插值)。

一般人都会提到该形变会使薄板的弯曲能量最小，这里有个最容易进入的误区：是把这张2D图像看作薄板没错，但弯曲能量指的并不是N个点形变到对应位置所产生在薄板内的“弯曲”。事实上，该样条函数是对每一维的坐标变化分别进行插值。我们把每一维的形变(x或y坐标的变化)施加于垂直于薄板的方向，此时使得弯曲能量最小的形变给出了该维的插值。

1.TPS原理介绍：首先看基础函数,有兴趣的可以上网画一下该函数的图像。此函数的特点是。

现在假想在一块薄板上放一个正方形框架，现在将薄板的两个点固定在该框架两个对角的上方，并把另薄板两个点固定在该框架另两个对角的下方，此时薄板会产生垂直方向上的形变和弯曲此时，弯曲能量最小的形变函数恰恰可以写成

其中Dk为框架四个角的坐标，因为该z(x,y)是以下弯曲能量函数的最小值

我们可以想象把这个形变嵌入到平面中去，比如把z(x,y)看作点(x,y)的x坐标的变化。如下图，两个对角上移，两个对角下移。注意此时所有的y坐标都不变，因为我们把薄板垂直方向上的形变放到了x坐标上。

同理我们可以对y坐标进行形变，得出整体的2D的插值。

2.计算函数系数

我们知道了当有N个点的形变约束条件时，TPS可以写成的形式。那么系数w的求解就变得简单了，无非是解一个方程组使得N个点形变到对应位置。

现在考虑第一张图上有k个点 {tj|j=1...k} (每个点为2*1的向量)对应到第二章图上的{yi|i=1...k}，即有2k个插值约束。同时定义现在我们求形变函数Phi，使得对应点匹配

因为上面说了此函数对x，y坐标分别插值，所以

其中t是2*1的向量，.c和A定义了对应点之间的仿射变换。由于有2k+6个参数需要求解，而我们只有2k个插值约束，我们另定义以下约束条件：

这些约束的存在是因为有了仿射变换的存在，TPS系数可以归一化。于是我们要求解的方程是（即对应点在形变后匹配）：

则系数可通过简单的逆矩阵求得

可以证明该Phi函数是以下弯曲能量泛函的最小值

*更为平滑的TPS有时我们不需要将对应点严格的匹配，我们允许对应点在形变后有一定的距离，从而得到更为平滑的形变，此时我们需要最小化的函数就变成了：

第一项约束了对应点在形变后的距离不能太大，第二项约束了弯曲程度，而我们需要的平滑程度由\lambda参数决定。不难推导出，要最小化此目标方程，只需要改动

3.统计分析：Principal warps

频谱分析是数理统计最常用的方法。频谱分析广义来说就是对一个矩阵做特征值分解。分解出的特征向量为原始数据提供了一组正交基。与一般的正交基不同，一般来说这些特征向量给出了类似傅里叶变换中不同尺度的正交基（即为频谱），也就是说这些特征向量如果按照对应特征值大小(频谱的能量)排序的话，给出了由低频到高频的基向量。因为一般来说如果对一个矩阵A进行特征分解，那么最小特征值所对应的特征向量会是

的解,反之也一样，最大特征值所对应的特征向量会是argmax的解。

比如对协方差矩阵求特征分解就会得出数据的主成分，并随着特征值变小得出其余的“副”成分。对一张图或者一个曲面的laplace算子求特征值分解会得出曲面由高频到低频的震动模式。

同理这种方法在TPS中也可以得到应用。我们定义左上角k*k的矩阵为B：弯曲能量矩阵。可以证明弯曲能量的最小值为。

我们对B进行特征值分解，按照其非零特征值从小到大排序，得到的特征向量为，这些特征向量叫做principal warp eigenvectors（主弯曲形变特征向量），其对应的特征值叫做弯曲能量。而以下方程则称为principal warp(主弯曲形变函数)

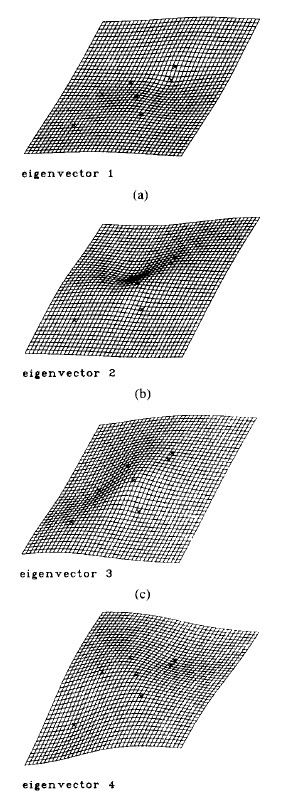
这些主弯曲形变函数不取决与第二图k个点的位。他们可以为TPS非仿射变换部分提供一组形变的正交基。我们可以画出每个principal warp函数

可见，对应弯曲能量小的弯曲形变函数给出了更为平滑，大尺度的低频形变，而对应弯曲能量大的形变函数给出了小尺度高频的形变。

*有兴趣的可以了解下partial warp，其实partial warp不是什么新概念，无非是给出第二张图后，其TPS形变可以投影到这些主形变上。

*Relative warp

简要介绍一下relative warp(相对弯曲形变)的概念。首先需要了解的是在一般度量空间内的PCA。我们定义在一个metric space中两点的距离定义为

而范数定义为

。

不同于一般的欧式空间，在这种度量空间内衡量距离的方式有特殊的侧重。比如A矩阵是一个高斯的协方差矩阵，那么这个度量空间定义的距离即为Mahalanobis距离(即在方差小的方向上，在欧式空间距离很近的点也会产生很大的距离)。

我们如何对此空间的点群做PCA呢。一般的答案是将其转化为欧式空间中的点，即，然后再做PCA。即最后特征值分解是针对而做的。

而relative warp的基本想法是：当我们有一组形状(shape)时，我们不直接将其表示在欧式空间中。我们先求出其平均形状的弯曲能量矩阵B，并将这些形状表现在以B为度量张量（也就是上一段中的矩阵A）的度量空间中。比如将替换成。我们知道

所以其在此度量空间中，距离就被定义为

即更强调弯曲能量（特征值）小的形变的成分，也就是说这个度量空间更侧重于大尺度形变的差异。同理也可以直接用B作为度量张量，此时则更侧重小尺度的形变差异。

 

参考：Fred Bookstein的“Principal Warps: Thin-Plate Splines and the Decomposition of Deformations”

Dryden和Mardia的“Statistical shape analysis”