数据拟合教程

数据拟合教程
1.搭建环境
1.1所需软件
1) VMware Workstation Pro（VMware-workstation-full-12.0.0）
2) CentosIOS（详细版本CentOS-7-x86_64-DVD-1611）
3) FileZilla Client（文件上传软件）
4) Putty（SSH链接工具）
以上软件请到网上自行搜索下载，安装虚拟系统指定的目录为：E:\vmos\centos01，IP地址规划为：192.168.174.100。也可自行进行修改。
1.2详细步骤
1.2.1安装VMware
下载相关软件后，按照提示进行操作即可，此处省略几万字。
1.2.2安装FileZilla
也省略几千字
1.2.3新建centos系统虚拟机
安装完VMware软件，启动之后的主界面如下：

创新建的虚拟机，按照提示点击“下一步”

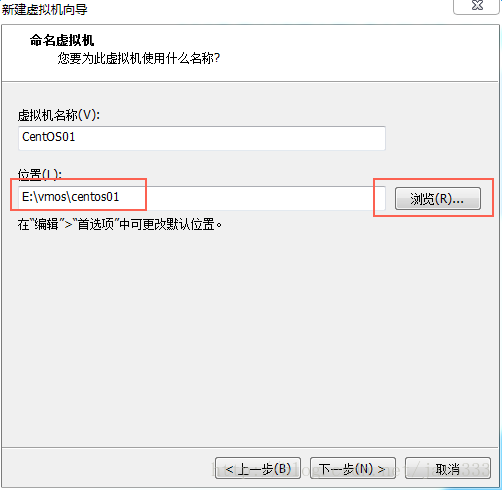
为减少系统的性能影响，移除一些不必要的设备硬件

此处为了方便克隆更多的系统，点击生成，得到一个MAC地址。


选择IOS镜像的位置

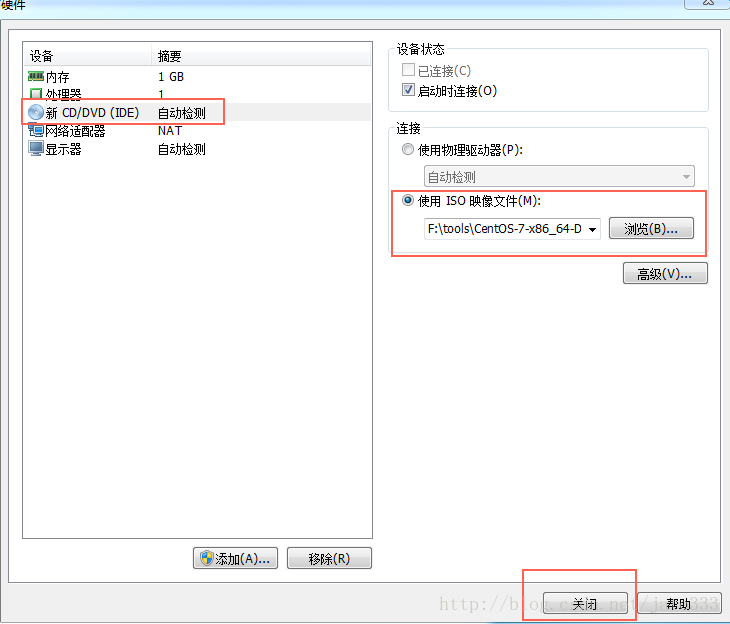
1.2.4开始安装

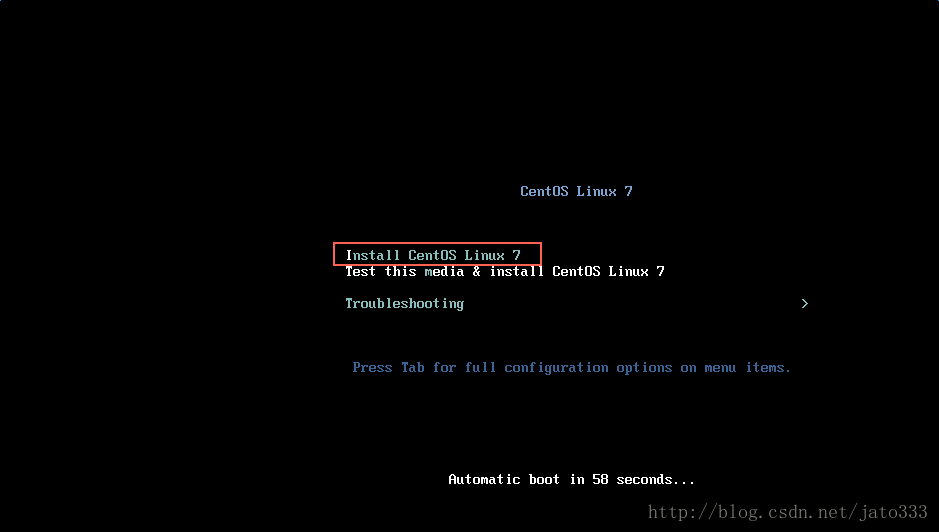
设置安装过程中使用的语言提示

设置系统时区，设置好之后，点击“Done”


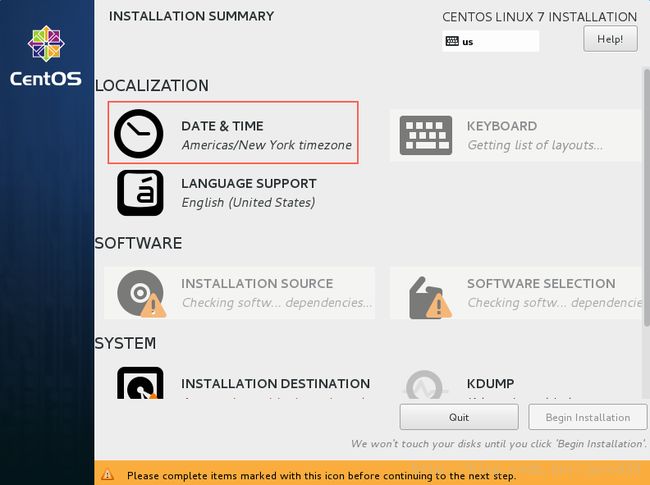
设置系统支持的语言，选择简体中文，设置好之后，点击“Done”


选择以下安装源，不用改动，点击“Done”


接下来进行网络相关的设置


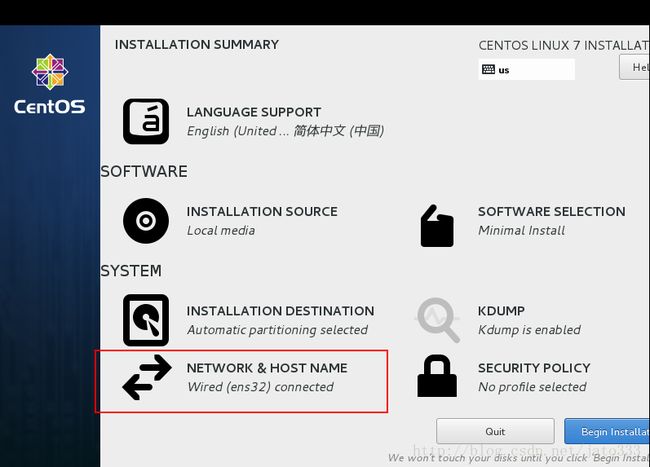
使用静态IP


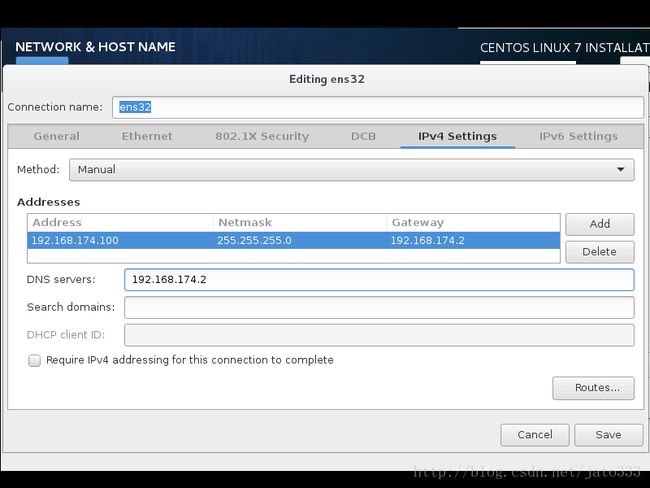
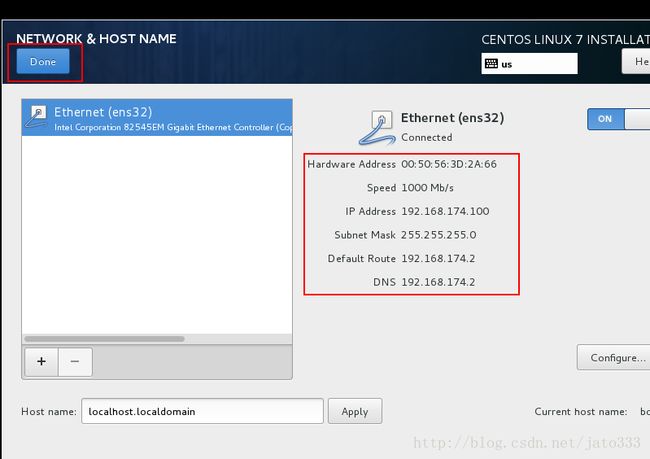
选择需要安装的软件，预测的图表需要图形包的支持


点击“Begin Install”启动安装过程

设置以下root账户的密码


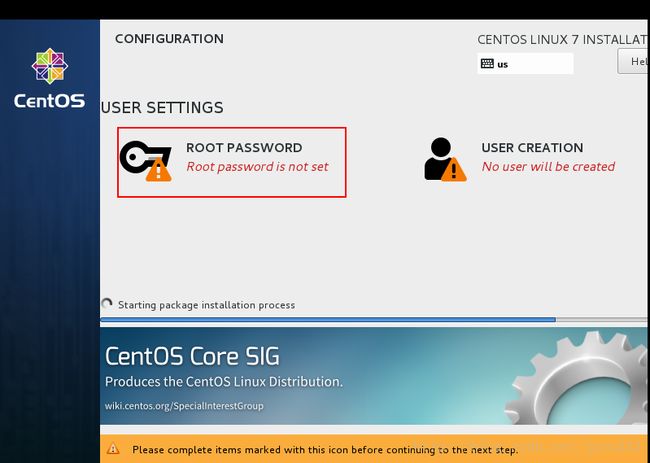
为方便我设置的密码为123，此密码是root账户的密码。设置好密码，点击两次“Done”。
安装开始了，需要等待一会，

喝杯caffe，回来看见了此界面，点击“Reboot”。重启之后，需要输入账号和密码


至此，我们已经成功安装了centos系统。

1.2.5配置centos系统
右击，选择“打开终端”，切换到root账号，输入命令:su –回车
输入密码：123回车
看到#，我们已成功进入到系统了，关闭并禁止自启动防火墙服务
Systemctl stop firewalld.service
Systemctl disable firewalld.service

查看以下IP地址:ip addr

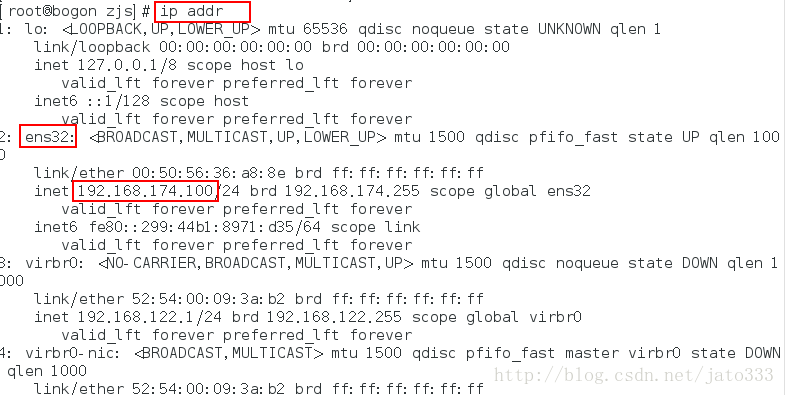
IP地址就是我们刚才设置的192.168.174.100。

1.2.6连接centos系统
为方便复制、粘贴命令，我们使用putty连接此服务器。

同样输入账户密码，连接成功了。

查看python版本：python –version

1.2.7安装python相关包
需要使用到的一些包，按照下面的命令执行即可：(不同的Iso镜像，稍有不同)
yum update -y && yum install zip unzip python python-devel gcc glibc.i686 epel-release.noarch
yum update -y && yum install -y tkinter
yum -y install python-pip

Yum clean all，清理一下下载的缓存。先前的安装中，我们安装了一个很重要的包工具pip，此工具可以方便地为我们安装python所需要的包软件以及相关的依赖包等。按照顺序依次执行即可，安装过程中，会受网络的影响出现红色告警文字，不用担心，多尝试几次即可。
pip install –upgrade pip

pip install scikit-learn numpy scipy
pip install tflearn
pip install h5py
pip search matplotlib
pip install matplotlib
pip install pandas
pip install seaborn
pip install tensorflow
pip install –upgrade tensorboard

说明：
python的科学计算有三剑客：numpy，scipy，matplotlib。
numpy负责数值计算，矩阵操作等；
scipy负责常见的数学算法，插值、拟合等；
matplotlib负责画图；
pandas负责数据的读取；
1.2.8测试
以上所有操作完成之后，我们需要的环境就已经搭建完毕。测试一下吧。
 
2.基础知识
2.1矩阵
在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合。高等代数学中的常见工具，也常见于统计分析等应用数学学科中。
2.1.1定义
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：

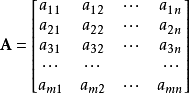
2.1.2基本运算
矩阵运算在科学计算中非常重要，而矩阵的基本运算包括矩阵的加法，减法，数乘，转置，共轭和共轭转置。
2.1.2.1加法

2.1.2.2减法

2.1.2.3数乘

矩阵的数乘满足以下运算律：



矩阵的加减法和矩阵的数乘合称矩阵的线性运算。
2.1.2.4转置
把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵，这一过程称为矩阵的转置

矩阵的转置满足以下运算律：



2.1.2.5共轭
矩阵的共轭定义为:

共轭根式
当 都是有理根式，而 、 中至少有一个是无理根式时，称
和 互为“共轭根式”。
共轭矩阵
共轭矩阵又称Hermite阵。Hermite阵中每一个第i 行第j 列的元素都与第j 行第i 列的元素的共轭相等。
一个2×2复数矩阵的共轭如下所示 ： ，则
2.1.2.6共轭转置
矩阵的共轭转置定义为：

也可以写为：

一个2×2复数矩阵的共轭如下所示：

则

2.1.3乘法
两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵，它们的乘积C是一个m×p矩阵
，它的一个元素：

并将此乘积记为:
.
例如：

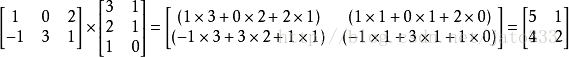
矩阵的乘法满足以下运算律：
结合律：

左分配律：

右分配律：

矩阵乘法不满足交换律。
3.数据预测案例
3.1预测特定房子的价值

我们想预测特定房子的价值，预测依据是房屋面积。
我们有下面的数据集：
编号 平方英尺 价格
1 150 6450
2 200 7450
3 250 8450
4 300 9450
5 350 11450
6 400 15450
7 600 18450

根据上面的数据，我们来预测700平方英尺值的价格数值是多少？
在线性回归中，我们都知道必须在数据中找出一种线性关系，以使我们可以得到a和b。 我们的假设方程式如下所示：
y(x)=a+bx
其中： y(x)是关于特定平方英尺的价格值（我们要预测的值），意思是价格是平方英尺的线性函数； a是一个常数； b是回归系数。
思路：
1)把数据存储成一个.csv文件，名字为input_data.csv 中，X值（平方英尺：square_feet）、Y值（价格：price），这一步很简单的，可以先用Excel来存储数据，记得写上列名。之后保存的时候另存为csv格式即可。
2)编写python代码(完整代码如下，#开始的部分为注视，红色粗体部分内容在运行前可删除)

中文显示乱码处理

-- encoding=utf-8 --

程序中要用到下面的包

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import datasets, linear_model

M = []
N = []

将.csv数据读入Pandas数据帧并转换为X_parameter和Y_parameter数据返回

def get_data(file_name):
data = pd.read_csv(file_name)
X_parameter = []
Y_parameter = []
for single_square_feet ,single_price_value in zip(data[‘square_feet’],data[‘price’]):
X_parameter.append([float(single_square_feet)])
Y_parameter.append(float(single_price_value))
return X_parameter,Y_parameter

把X_parameter和Y_parameter拟合为线性回归模型。我们要写一个函数，输入为X_parameters、Y_parameter和

要预测的平方英尺值，返回a、b和预测出的价格值。

这里使用的是scikit-learn机器学习算法包。该算法包是目前python实现的机器算法包最好的一个。

创建一个线性模型，用我们的X_parameters和Y_parameter训练它。

创建一个名称为predictions的字典，存着a、b和预测值，并返回输出

def linear_model_main(X_parameters,Y_parameters,predict_value):
regr = linear_model.LinearRegression() #定义使用的线性模型
regr.fit(X_parameters, Y_parameters) #训练模型
predict_outcome = regr.predict(predict_value) #测试数据，返回标记
predictions = {}
predictions[‘intercept’] = regr.intercept_ #则存放截距
predictions[‘coefficient’] = regr.coef_ #存放相关系数
predictions[‘predicted_value’] = predict_outcome
return predictions

调用函数，要预测的平方英尺值为700

X,Y = get_data(‘input_data.csv’)
for i in range(600,1000,50):
predictvalue = i
result = linear_model_main(X,Y,predictvalue)
print “Intercept value ” , result[‘intercept’]
print “coefficient” , result[‘coefficient’]
print “Predicted value: “,result[‘predicted_value’]

M.append([predictvalue])
N.append(np.floor(result[‘predicted_value’]))

加入预测的数值和结果到图形显示区域中

X.append([predictvalue])
Y.append(np.floor(result[‘predicted_value’]))

这里，Intercept value（截距值）就是a的值

coefficient value（系数）就是b的值

得到预测的价格值为21915.4255

意味着我们已经把预测房子价格的工作做完了！

为了验证，需要看看我们的数据怎么拟合线性回归。

所以需要写一个函数，输入为X_parameters和Y_parameters，显示出数据拟合的直线。

def show_linear_line(X_parameters,Y_parameters):
regr = linear_model.LinearRegression()
regr.fit(X_parameters, Y_parameters)
plt.scatter(X_parameters,Y_parameters,color=’blue’)
plt.plot(X_parameters,regr.predict(X_parameters),color=’red’,linewidth=4)
plt.xticks(X_parameters)
plt.yticks(Y_parameters)

regr2 = linear_model.LinearRegression()
regr2.fit(M, N)
plt.scatter(M,N,color=’blue’)
plt.plot(M,regr2.predict(M),color=’green’,linestyle=”:”,linewidth=2)dd
plt.xticks(M)
plt.yticks(N)

plt.show()
show_linear_line(X,Y)

调用一下show_linear_line函数吧：show_linear_line(X,Y)

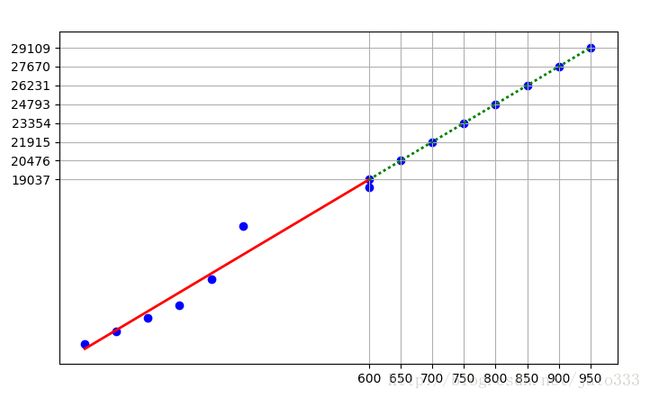
从图形中，我们很直观地看到了700平方英尺房屋对应的房价数值为21915。
实线部分表示训练数据，虚线部分表示预测数据。
3.2拟合温度曲线

根据某地每月的平均温度[17, 19, 21, 28, 33, 38, 37, 37, 31, 23, 19, 18]拟合温度函数。
思路：
scipy.optimize提供了函数最小值(标量或多维)、曲线拟合和寻找等式的根的有用算法。

可以看出温度是以年为单位的周期为12的正弦函数，构建函数y=a*sin(x*pi/6+b)+c，使用optimize.curve_fit函数求出a、b、c的值。

实现代码：

-- encoding=utf-8 --

import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
x=np.arange(1,13,1)
x1=np.arange(1,13,0.1)
ymax=np.array([17, 19, 21, 28, 33, 38, 37, 37, 31, 23, 19, 18 ])
def fmax(x,a,b,c):
return a*np.sin(x*np.pi/6+b)+c
fita,fitb=optimize.curve_fit(fmax,x,ymax,[1,1,1])
print(fita)
plt.plot(x,ymax)
plt.plot(x1,fmax(x1,fita[0],fita[1],fita[2]))
plt.show()
以下为拟合曲线，求出a b c的值为[ 10.93254952 -1.9496096 26.75]
 
3.3拟合对数曲线
对数函数：
y = a * log(x) + b
实现代码：

-- encoding=utf-8 --

import matplotlib.pyplot as plt
import numpy
from scipy import log
from scipy import optimize

def polyfit(x, a, b):
y = a * log(x) + b
return y

x=[ 1 ,2 ,3 ,4 ,5 ,6]
y=[ 2.5 ,3.51 ,4.45 ,5.52 ,6.47 ,7.51]

fita,fitb=optimize.curve_fit(polyfit,x,y,[1,1])

print(fita)
plt.scatter(x,y,color=’blue’)
plt.plot(x,y)
plt.scatter(x,polyfit(x,fita[0],fita[1]),color=’yellow’)
plt.plot(x,polyfit(x,fita[0],fita[1]),linestyle=’:’,color=’red’)
plt.show()
运行显示结果如下，a=2.72873961,b=2.00115611

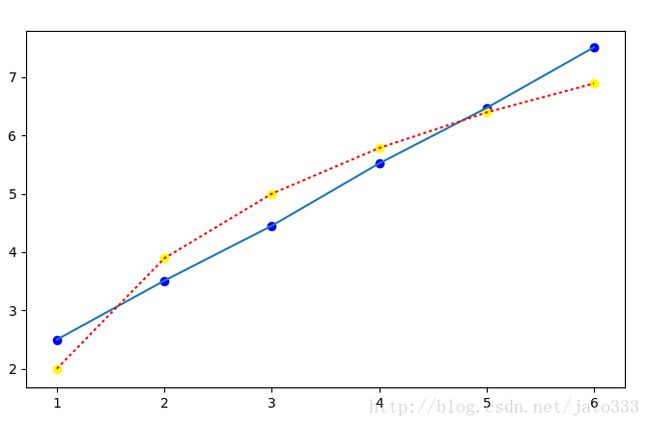
3.4多元线性回归
1、多元线性回归模型定义
当y值的影响因素不唯一时,采用多元线性回归模型。
y =β0+β1x1+β2x2+…+βnxn
2、销售数据样例
TV Radio Newspaper Sales
1 230.1 37.8 69.2 22.1
2 44.5 39.3 45.1 10.4
3 17.2 45.9 69.3 9.3
4 151.5 41.3 58.5 18.5
… … … … …
191 39.5 41.1 5.8 10.8
192 75.5 10.8 6 9.9
193 17.2 4.1 31.6 5.9
194 166.8 42 3.6 19.6
195 149.7 35.6 6 17.3
196 38.2 3.7 13.8 7.6
商品销售额可能与电视广告投入,收音机广告投入,报纸广告投入有关系,可假设公式：
sales =β0+β1 * TV +β2 * Radio +β3 * Newspaper
3、分析数据
1)特征：
 TV：对于一个给定市场中单一产品，用于电视上的广告费用（以千为单位）
 Radio：在广播媒体上投资的广告费用
 Newspaper：用于报纸媒体的广告费用
2)响应：
 Sales：对应产品的销量
在这个案例中，我们通过不同的广告投入，预测产品销量。因为响应变量是一个连续的值，所以这个问题是一个回归问题。数据集一共有200个观测值，每一组观测对应一个市场的情况。
这里我们首先选择TV、Radio、Newspaper 作为特征，Sales作为观测值

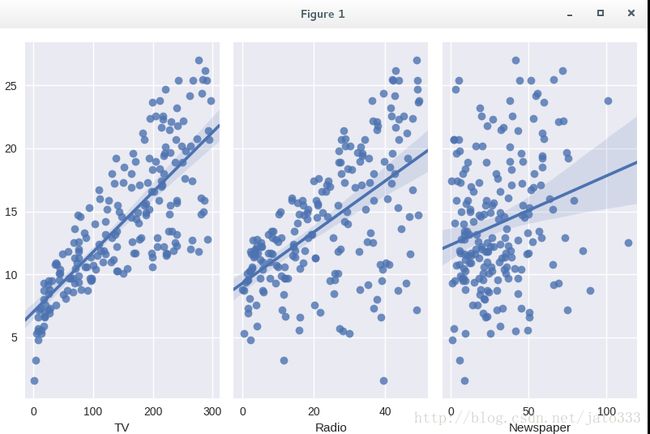
seaborn的pairplot函数绘制X的每一维度和对应Y的散点图。通过设置size和aspect参数来调节显示的大小和比例。可以从图中看出，TV特征和销量是有比较强的线性关系的，而Radio和Sales线性关系弱一些，Newspaper和Sales线性关系更弱。通过加入一个参数kind=’reg’，seaborn可以添加一条最佳拟合直线和95%的置信带。
4、线性回归模型
 优点：快速；没有调节参数；可轻易解释；可理解。
 缺点：相比其他复杂一些的模型，其预测准确率不是太高，因为它假设特征和响应之间存在确定的线性关系，这种假设对于非线性的关系，线性回归模型显然不能很好的对这种数据建模。
线性模型表达式： y=β0+β1x1+β2x2+…+βnxnn
其中
• y是响应
• β0是截距
• β1是x1的系数，以此类推
在这个案例中： y=β0+β1 * TV +β2 * Radio +β3 * Newspaper
5、回归问题的评价测度
(1) 评价测度
对于分类问题，评价测度是准确率，但这种方法不适用于回归问题。我们使用针对连续数值的评价测度(evaluation metrics)。
这里介绍3种常用的针对线性回归的测度。
1) 平均绝对误差(Mean Absolute Error, MAE)
1) 均方误差(Mean Squared Error, MSE)
2) 均方根误差(Root Mean Squared Error, RMSE)
这里我使用RMES。
6、完整代码

-- encoding=utf-8 --

import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import metrics

使用pandas加载数据集

data = pd.read_csv(‘/renyuwo/Advertising.csv’)

选择TV、Radio、Newspaper 作为特征，Sales作为观测值

sns.pairplot(data, x_vars=[‘TV’,’Radio’,’Newspaper’], y_vars=’Sales’, size=7, aspect=0.8, kind=’reg’)

使用pandas来构建X(特征向量)和y(标签列)

X = data[[‘TV’, ‘Radio’, ‘Newspaper’]]
y = data[‘Sales’]

构建训练集与测试集(默认： 75% 的数据进行训练 25% 的数据进行测试)

X_train,X_test, y_train, y_test = train_test_split(X, y, random_state=1)

sklearn的线性回归

linreg = LinearRegression()
model=linreg.fit(X_train, y_train)

预测

y_pred = linreg.predict(X_test)

使用RMES评价测度

sum_mean=0
for i in range(len(y_pred)):
sum_mean+=(y_pred[i]-y_test.values[i])**2
sum_erro=np.sqrt(sum_mean/50)

做ROC曲线

plt.figure()
plt.plot(range(len(y_pred)),y_pred,’b’,label=”predict”)
plt.plot(range(len(y_pred)),y_test,’r’,label=”test”)
plt.legend(loc=”upper right”)
plt.xlabel(“the number of sales”)
plt.ylabel(‘value of sales’)
plt.show()
运行效果如下：

最后的结果如下：

-- encoding=utf-8 --

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

x=tf.placeholder(tf.float32,[None,1])

W=tf.Variable(tf.zeros([1,1]))
b=tf.Variable(tf.zeros([1]))

y=tf.matmul(x,W)+b

y_=tf.placeholder(tf.float32,[None,1])

cost=tf.reduce_sum(tf.pow((y-y_),2))

train_step=tf.train.GradientDescentOptimizer(0.0001). minimize(cost)

init = tf. global_variables_initializer ()

with tf.Session() as sess:
sess.run(init)
for I in range(100):
xs=np.array([[i]])
ys=np.array([[2*i+ tf.random_normal([1])]])
sess.run(train_step,feed_dict={x:xs,y_:ys})
4.6tensorboard可视化
上面的代码已经成功运行了，那有没有一种可视化的工具，让我们更加深入了解前面的内容？google作为一个伟大的企业，已经为我们考虑到了，那就是tensorboard。
当前的版本已经更新到1.0.1，很多api接口发生了变化，具体参考地址为：https://morvanzhou.github.io/tutorials/machine-learning/tensorflow/4-1-tensorboard1/。

-- encoding=utf-8 --

import tensorflow as tf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

with tf.name_scope(‘x’):
x=tf.placeholder(tf.float32,[None,1])

with tf.name_scope(‘W’):
W=tf.Variable(tf.zeros([1,1]))

with tf.name_scope(‘b’):
b=tf.Variable(tf.zeros([1]))

with tf.name_scope(‘y’):
y=tf.matmul(x,W)+b

with tf.name_scope(‘y_’):
y_=tf.placeholder(tf.float32,[None,1])

with tf.name_scope(‘cost’):
cost=tf.reduce_sum(tf.pow((y-y_),2))

with tf.name_scope(‘train_op’):
train_op=tf.train.GradientDescentOptimizer(0.0001). minimize(cost)

init = tf. global_variables_initializer ()

with tf.Session() as sess:
writer = tf.summary.FileWriter(“/zjs/log/”, sess.graph)
sess.run(init)
for i in range(100):
xs=np.array([[i]])
ys=np.array([[2*i]])

sess.run(train_step,feed_dict={x:xs,y_:ys})

用putty开启一个新的session连接，输入
tensorboard –logdir=’/zjs/log’
运行后，会在相应的目录里生成一个文件，在浏览器中输入
http://192.168.174.100:6006/
我们可以看见可视化的tensorflow了。Tensorboard可视化模块详情：
• Scalars: 展示训练过程中的统计数据（最值，均值等）变化情况
• Image: 展示训练过程中记录的图像
• Audio: 展示训练过程中记录的音频
• Histogram: 展示训练过程中记录的数据分布图，更细节的取值概率信息
• Distribution：显示取值范围
编码说明：
• Summary：所有需要在TensorBoard上展示的统计结果。
• tf.name_scope()：为Graph中的Tensor添加层级，TensorBoard会按照代码指定的层级进行展示，初始状态下只绘制最高层级的效果，点击后可展开层级看到下一层的细节。
• tf.summary.scalar()：添加标量统计结果。
• tf.summary.histogram()：添加任意shape的Tensor，统计这个Tensor的取值分布。
• tf.summary.merge_all()：添加一个操作，代表执行所有summary操作，这样可以避免人工执行每一个summary op。
• tf.summary.FileWrite：用于将Summary写入磁盘，需要制定存储路径logdir，如果传递了Graph对象，则在Graph Visualization会显示Tensor Shape Information。执行summary op后，将返回结果传递给add_summary()方法即可。