贝叶斯网络推理之后验概率问题(基于FullBNT-1.0.4的MATLAB实现)
题目:贝叶斯网络推理之后验概率问题(基于FullBNT-1.0.4的MATLAB实现)
看本篇前,可以简单浏览《贝叶斯网络与最大可能解释(MPE)问题》,通过与MPE问题的对比了解后验概率问题的概念;如果想简单了解贝叶斯网络推理算法,可以阅读《贝叶斯网络推理算法简单罗列》,尤其是常用的联结树算法(junction tree),在文中附录摘有详细解释。
在BNT工具箱中,后验概率问题的求解函数是marginal_nodes,该函数在不同的推理引擎下进行重载:
stable_ho_inf_engine/marginal_nodes
pearl_unrolled_dbn_inf_engine/marginal_nodes
pearl_dbn_inf_engine/marginal_nodes
kalman_inf_engine/marginal_nodes
jtree_unrolled_dbn_inf_engine/marginal_nodes
jtree_dbn_inf_engine/marginal_nodes
hmm_inf_engine/marginal_nodes
frontier_inf_engine/marginal_nodes
ff_inf_engine/marginal_nodes
cbk_inf_engine/marginal_nodes
bk_inf_engine/marginal_nodes
bk_ff_hmm_inf_engine/marginal_nodes
smoother_engine/marginal_nodes
jtree_sparse_2TBN_inf_engine/marginal_nodes
jtree_2TBN_inf_engine/marginal_nodes
hmm_2TBN_inf_engine/marginal_nodes
filter_engine/marginal_nodes
var_elim_inf_engine/marginal_nodes
stab_cond_gauss_inf_engine/marginal_nodes
quickscore_inf_engine/marginal_nodes
pearl_inf_engine/marginal_nodes
likelihood_weighting_inf_engine/marginal_nodes
jtree_sparse_inf_engine/marginal_nodes
jtree_limid_inf_engine/marginal_nodes
jtree_inf_engine/marginal_nodes
global_joint_inf_engine/marginal_nodes
gibbs_sampling_inf_engine/marginal_nodes
gaussian_inf_engine/marginal_nodes
enumerative_inf_engine/marginal_nodes
cond_gauss_inf_engine/marginal_nodes
belprop_mrf2_inf_engine/marginal_nodes
belprop_inf_engine/marginal_nodes
belprop_fg_inf_engine/marginal_nodes
有关marginal_nodes的使用例子在目录\FullBNT-1.0.4\BNT\examples\static中有多个文件,本人看了三个m文件:burglary.m、brainy.m、sprinkler1.m。就marginal_nodes函数的使用而言,几个例子大同小异,以下就以burglary.m为例来说明。
在《贝叶斯网络推理之最大可能解释问题(基于FullBNT-1.0.4的MATLAB实现)》中提到,BNT工具箱里的“草地潮湿原因”和“是窃贼还是地震”两个例子在网上流传较广,而burglary.m就是“是窃贼还是地震”:
WetGrass相关:
http://blog.csdn.net/a_302/article/details/17916569
https://zhidao.baidu.com/question/1769951750149622540.html
http://blog.sina.com.cn/s/blog_7600796a0100p5lx.html
http://blog.csdn.net/yefengnidie/article/details/4247254
https://wenku.baidu.com/view/379405dcd15abe23482f4d1c.html
Burglary相关:
https://wenku.baidu.com/view/4a775b70336c1eb91a375d33.html
https://my.oschina.net/SnifferApache/blog/343756
例子burglary.m的源码如下:
% Burglar alarm example
N = 5;
dag = zeros(N,N);
E = 1; B = 2; R = 3; A = 4; C = 5;
dag(E,[R A]) = 1;
dag(B,A) = 1;
dag(A,C)=1;
% true = state 1, false = state 2
ns = 2*ones(1,N); % binary nodes
bnet = mk_bnet(dag, ns);
bnet.CPD{E} = tabular_CPD(bnet, E, [0.1 0.9]);
bnet.CPD{B} = tabular_CPD(bnet, B, [0.01 0.99]);
%bnet.CPD{R} = tabular_CPD(bnet, R, [0.65 0.00001 0.35 0.99999]);
bnet.CPD{R} = tabular_CPD(bnet, R, [0.65 0.01 0.35 0.99]);
bnet.CPD{A} = tabular_CPD(bnet, A, [0.95 0.8 0.3 0.001 0.05 0.2 0.7 0.999]);
bnet.CPD{C} = tabular_CPD(bnet, C, [0.7 0.05 0.3 0.95]);
engine = jtree_inf_engine(bnet);
ev = cell(1,N);
ev{C} = 1;
engine = enter_evidence(engine, ev);
mE = marginal_nodes(engine, E);
mB = marginal_nodes(engine, B);
fprintf('P(E|c)=%5.3f, P(B|c)=%5.3f\n', mE.T(1), mB.T(1))
ev{C} = 1;
ev{R} = 1;
engine = enter_evidence(engine, ev);
mE = marginal_nodes(engine, E);
mB = marginal_nodes(engine, B);
fprintf('P(E|c,r)=%5.3f, P(B|c,r)=%5.3f\n', mE.T(1), mB.T(1))
if 0
nsamples = 100;
samples = zeros(nsamples, 5);
for i=1:nsamples
samples(i,:) = cell2num(sample_bnet(bnet))';
end
end
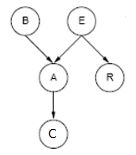
前20行就是人为地生成了一个贝叶斯网络(第3~8行规定了贝叶斯网络结构,第14~19行规定了贝叶斯网络参数)。这个贝叶斯网络是“是窃贼还是地震”模型,初始化的贝叶斯网络结构如下(E—Earthquake, B—Burglary, R—Radio, A—Alarm, C--Call):
这里再多说几句贝叶斯网络参数的设定:

第14行表示发生地震的概率是0.1(不发生地震的概率是0.9);
第15行表示家里来盗贼的概率是0.01(不来盗贼的概率是0.99);
(注:这两个概率设定似乎与常理不符,应该反过来才是,我们暂且不去管它)
第17行初始化无线电广播发生地震(Radio=True)的概率,如下:
|
Radio=True |
Radio=False |
Earthquake=True |
0.65 |
0.35 |
Earthquake=False |
0.01 |
0.99 |
即发生地震时(Earthquake=True)无线电广播发生地震(Radio=True)的概率是0.65(不广播的概率是0.35),不发生地震时(Earthquake=False)无线电广播发生地震(Radio=True)的概率是0.01(不广播的概率是0.99);
第18行初始化警铃响了(Alarm=True)的概率,如下:
|
Alarm=True |
Alarm= False |
Burglary=True, Earthquake=True |
0.95 |
0.05 |
Burglary=True, Earthquake=False |
0.8 |
0.2 |
Burglary=False, Earthquake=True |
0.3 |
0.7 |
Burglary=False, Earthquake=False |
0.001 |
0.999 |
(注:Burglary和Earthquake的先后顺序不太确定,但个人认为此顺序更合理)
即家里来了盗贼(Burglary=True)又发生地震(Earthquake=True)时警铃响(Alarm=True)的概率是0.95(警铃不响的概率是0.05),家里来了盗贼(Burglary=True)但没发生地震(Earthquake=False)时警铃响(Alarm=True)的概率是0.8(警铃不响的概率是0.2),家里没来盗贼(Burglary=False)但发生地震(Earthquake=True)时警铃响(Alarm=True)的概率是0.3(警铃不响的概率是0.7,至所以采用此Burglary和Earthquake先后顺序是因为个人感觉警铃应该主要是用来防盗的吧),家里没来盗贼(Burglary=False)也没发生地震(Earthquake=False)时警铃响(Alarm=True)的概率是0.001(警铃不响的概率是0.999);
第19行初始化邻居给房子主人打电话(Call=True)的概率如下:
|
Call=True |
Call=False |
Alarm=True |
0.7 |
0.3 |
Alarm= False |
0.05 |
0.95 |
即警铃响了(Alarm=True)邻居给房子主人打电话(Call=True)的概率是0.7(不打电话的概率是0.3),警铃没响邻居(Alarm= False)给房子主人打电话(Call=True)的概率是0.05(不打电话的概率是0.95);
第22行生成联结树推理引擎engine;
第23行初始化一个cell类型的证据变量;
第24~28行是在接到邻居电话的情况下(ev{C} = 1;)分别推测发生地震的概率(第26行)和家里来盗贼的概率(第27行),并输出(第28行);
第30~35行是在接到邻居电话(ev{C} = 1;)并且听到广播说发生地震了(ev{R}= 1;)的情况下分别推测发生地震的概率(第33行)和家里来盗贼的概率(第34行),并输出(第35行);
运行burglary.m,命令行窗口(Command windows)输出如下:
>> burglary
P(E|c)=0.331, P(B|c)=0.077
P(E|c,r)=0.970, P(B|c,r)=0.029
这个结果并不符合常理,可以发现,在只接到邻居电话的情况下,推测出发生地震的概率是0.331,家里来盗贼的概率是0.077;在接到邻居电话并听到广播发生地震的情况下,推测出发生地震的概率是0.970,家里来盗贼的概率是0.029;后者还可以接受,但前者是不符合常理的,接到邻居电话后推测的结果居然是发生地震的概率比家里来盗贼的概率还大!!!
原因前面也提到了,主要是第14~15行两个概率设定有些问题:
这个概率设置意味着这个地区发生地震的概率比家里来盗贼的概率还要大,呃,好吧,或许人家治安特别好,又处在一个地震好发带呢?!
更合理的概率设置应该是把发生地震和家里来盗贼的概率交换一下,即:
这时候再运行burglary.m,命令行窗口(Command windows)输出如下:
>> burglary
P(E|c)=0.028, P(B|c)=0.547
P(E|c,r)=0.648, P(B|c,r)=0.346
这个结果就比较合理了,当接到邻居电话的时候更可能是家里来了盗贼(0.547>0.028),发生地震的概率(0.028)虽然比其先验概率(0.01)大,但仍然是很小的,毕竟地震本来就不常见;当接到邻居电话并听到广播发生地震时,发生地震的概率就比较大了(好吧,我们假设只有他家地震了,虽然听到广播,但就是感觉不到地面在震动)。
第38~44行是根据前面设定的贝叶斯网生成nsamples=100个采样数据,当然第38行用if 0将这段程序关掉了,默认不执行,因此我们就不去探讨了~
OK,到此讲完了,总结一下marginal_nodes函数的使用方法:
该函数要求输出两个参数:推理引擎和节点序号;但推理引擎并不是直接生成的,需要再调用enter_evidence函数对推理引擎加入证据变量,而enter_evidence的使用很简单,只需要输入推理引擎函数输出的引擎和证据变量即可。
但想要输出多个节点的联合概率怎么办呢?
我们运行以下程序:
% Burglar alarm example@20180304pm by jbb0523
clear all;close all;clc;
N = 5;
dag = zeros(N,N);
E = 1; B = 2; R = 3; A = 4; C = 5;
dag(E,[R A]) = 1;
dag(B,A) = 1;
dag(A,C)=1;
% true = state 1, false = state 2
ns = 2*ones(1,N); % binary nodes
bnet = mk_bnet(dag, ns);
bnet.CPD{E} = tabular_CPD(bnet, E, [0.1 0.9]);
bnet.CPD{B} = tabular_CPD(bnet, B, [0.01 0.99]);
%bnet.CPD{R} = tabular_CPD(bnet, R, [0.65 0.00001 0.35 0.99999]);
bnet.CPD{R} = tabular_CPD(bnet, R, [0.65 0.01 0.35 0.99]);
bnet.CPD{A} = tabular_CPD(bnet, A, [0.95 0.8 0.3 0.001 0.05 0.2 0.7 0.999]);
bnet.CPD{C} = tabular_CPD(bnet, C, [0.7 0.05 0.3 0.95]);
engine1 = jtree_inf_engine(bnet);
engine = jtree_inf_engine(bnet);
ev = cell(1,N);
ev{C} = 1;
ev{R} = 1;
engine = enter_evidence(engine, ev);
m_E_B_A = marginal_nodes(engine, [E,B,A]);
mpe_E_B_A =find_mpe(engine1, ev);
disp('m_E_B_A.T:');disp(m_E_B_A.T);
disp('mpe_E_B_A:');disp(mpe_E_B_A);
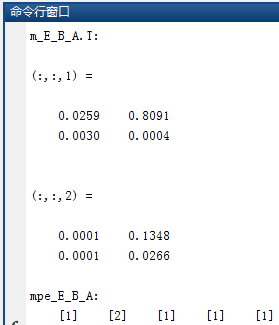
该程序的前20行与Burglary.m一样,第21~30行调用了marginal_nodes和find_mpe两个函数,只是第27行调用marginal_nodes时第二个参数设置为[E,B,A]三个节点,然后进行了输出:
输出结果m_E_B_A.T存储的是一组后验概率,若取后验概率最大值对应的节点值输出,则为MAP问题,由于证据变量为C和R,未知变量为E、B、A,二者的并集为所有节点,因此这个MAP等价于MPE问题(MAP问题与MPE问题的关系参见《贝叶斯网络与最大可能解释(MPE)问题》,函数find_mpe的使用方法参见《贝叶斯网络推理之最大可能解释问题(基于FullBNT-1.0.4的MATLAB实现)》)。
接下来解释一下m_E_B_A.T输出,程序中节点编号E=1,B=2,A=4,因此m_E_B_A.T这个三维矩阵最后一维是A,(:,:,1)指的是A=True时,(:,:,2)指的是A=False时,在(:,:,1)和(:,:,2)内部,行对就的E,列对应的B,因此0.0259对应的是E=True, B=True, A=True,0.8091对应的是E=True, B=False, A=True,0.0030对应的是E=False, B=True,A=True,0.0004对应的是E=False, B=False, A=True,同理,0.1348对应的是E=True, B=False,A=False,0.0266对应的是E=False, B=False, A=False,八个概率值之和为1,实际上就是当C=True、R=True时E、B、A联合概率分布,MAP就是取最大的,那么0.8091对就的是E=True, B=False, A=True,再翻译一下mpe_E_B_A的输出,1表示True,2表示False,合起来就是E=True, B=False, R=True,A=True, C=True,其中R和C是已知证据变量,这与MAP的输出结果是相同的,即证明了MAP与MPE的等价性。
但这种用法并不是任何时候都有效,比如把程序修改为:
% Burglar alarm example@20180304pm by jbb0523
clear all;close all;clc;
N = 5;
dag = zeros(N,N);
E = 1; B = 2; R = 3; A = 4; C = 5;
dag(E,[R A]) = 1;
dag(B,A) = 1;
dag(A,C)=1;
% true = state 1, false = state 2
ns = 2*ones(1,N); % binary nodes
bnet = mk_bnet(dag, ns);
bnet.CPD{E} = tabular_CPD(bnet, E, [0.1 0.9]);
bnet.CPD{B} = tabular_CPD(bnet, B, [0.01 0.99]);
%bnet.CPD{R} = tabular_CPD(bnet, R, [0.65 0.00001 0.35 0.99999]);
bnet.CPD{R} = tabular_CPD(bnet, R, [0.65 0.01 0.35 0.99]);
bnet.CPD{A} = tabular_CPD(bnet, A, [0.95 0.8 0.3 0.001 0.05 0.2 0.7 0.999]);
bnet.CPD{C} = tabular_CPD(bnet, C, [0.7 0.05 0.3 0.95]);
engine1 = jtree_inf_engine(bnet);
engine = jtree_inf_engine(bnet);
ev = cell(1,N);
ev{C} = 1;
% ev{R} = 1;
engine = enter_evidence(engine, ev);
m_E_B_A = marginal_nodes(engine, [E,B,R,A]);
mpe_E_B_A =find_mpe(engine1, ev);
disp('m_E_B_A.T:');disp(m_E_B_A.T);
disp('mpe_E_B_A:');disp(mpe_E_B_A);
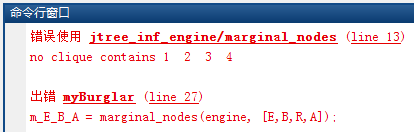
该程序相比于刚才减少了一个证据变量,增加了一个未知变量,运行之后程序会报错:
报错提示“no clique contains 1 2 3 4”,即没有团(clique)包括”1 2 3 4”。