【机器学习】降维技术-PCA
写在篇前
PCA即主成分分析技术,又称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标,其主要目的是为了减少数据的维数,而同时保持数据集最多的信息。这篇文章主要是整理PCA算法的理论、思想,然后通过Scikit-learn中的例子讲解PCA的使用。
数学基础
首先,我们需要了解几个重要的数学概念,其中均值、标准差、方差协方差应该是比较好理解的,主要是要注意对特征向量和特征值的理解。关于更详细的数学原理,可以直接参考博客 PCA的数学原理
均值(mean)
X ˉ = ∑ i = 1 n X i n \bar{X} = \frac{\sum_{i=1}^nX_i}{n} Xˉ=n∑i=1nXi
- \bar{X}:均值
- X_i:样本数据
- n n n:样本数
标准差(std)
衡量随机变量与其数学期望(均值)之间的偏离程度,注意区分样本方差、总体方差
s = ∑ i = 1 n ( X i − X ˉ ) 2 n − 1 s = \sqrt{\frac{\sum_{i=1}^n(X_i-\bar{X})^2}{n-1}} s=n−1∑i=1n(Xi−Xˉ)2
方差(var)
衡量随机变量与其数学期望(均值)之间的偏离程度
s 2 = ∑ i = 1 n ( X i − X ˉ ) 2 n − 1 s^2 = \frac{\sum_{i=1}^n(X_i-\bar{X})^2}{n-1} s2=n−1∑i=1n(Xi−Xˉ)2
协方差(cov)
衡量变量之间的相关性,协方差为0时,表示两随机变量不相关,>0表示正相关,反之负相关
c o v ( X , Y ) = ∑ i = 1 n ( X i − X ˉ ) ( Y i − Y ˉ ) n − 1 cov(X,Y) = \frac{\sum_{i=1}^n(X_i-\bar{X})(Y_i-\bar{Y})}{n-1} cov(X,Y)=n−1∑i=1n(Xi−Xˉ)(Yi−Yˉ)
C = ( c o v ( 1 , 1 ) c o v ( 1 , 2 ) c o v ( 1 , 3 ) ⋯ c o v ( 1 , n ) c o v ( 2 , 1 ) c o v ( 2 , 2 ) c o v ( 2 , 3 ) ⋯ c o v ( 2 , n ) c o v ( 3 , 1 ) c o v ( 3 , 2 ) c o v ( 3 , 3 ) ⋯ c o v ( 3 , n ) ⋮ ⋮ ⋮ ⋱ ⋮ c o v ( n , 1 ) c o v ( n , 2 ) c o v ( n , 3 ) ⋯ c o v ( n , n ) ) C = \begin{pmatrix} \color{#F00}{cov(1,1)} & \color{#0F0}{cov(1,2)} & \color{#F0F}{cov(1,3)} & \cdots & cov(1,n) \\ \color{#0F0}{cov(2,1)} & \color{#F00}{cov(2,2)} & cov(2,3) & \cdots & cov(2,n) \\ \color{#F0F}{cov(3,1)} & cov(3,2) &\color{#F00}{cov(3,3)} & \cdots & cov(3,n) \\ \vdots & \vdots& \vdots & \ddots & \vdots \\ cov(n,1) & cov(n,2) & cov(n,3) & \cdots & \color{#F00}{cov(n,n)} \end{pmatrix} C=⎝⎜⎜⎜⎜⎜⎛cov(1,1)cov(2,1)cov(3,1)⋮cov(n,1)cov(1,2)cov(2,2)cov(3,2)⋮cov(n,2)cov(1,3)cov(2,3)cov(3,3)⋮cov(n,3)⋯⋯⋯⋱⋯cov(1,n)cov(2,n)cov(3,n)⋮cov(n,n)⎠⎟⎟⎟⎟⎟⎞
特征向量(Eigenvectors)和特征值(Eigenvalues)
A v = λ v A 是 一 个 方 阵 , λ 是 一 个 标 量 。 此 处 λ 是 特 征 值 , v 是 特 征 向 量 Av = \lambda v \qquad A是一个方阵,\lambda是一个标量。此处\lambda是特征值,v是特征向量 Av=λvA是一个方阵,λ是一个标量。此处λ是特征值,v是特征向量
需要注意的是,只有方阵才能求出特征向量,但是,并不是每个方阵都有特征向量。假设我有一个n * n的矩阵,那么就有n个特征向量,并且一个矩阵中的所有特征向量都是相互垂直的,无论你的数据集中有多少特征。
实现PCA
上面数学概念解释比较模糊,具体一定要参考博客PCA的数学原理,下面用一个实例来实现PCA,数据集我们采用有名的Wine数据集
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import numpy as np
import matplotlib.pyplot as plt
df_wine = pd.read_csv('./wine', header=None) # 请自行下载数据
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.3,
random_state=0)
# 归一化,mean=0, var=1
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.fit_transform(X_test)
# 计算协方差,需要转置,注意理解
X_train_std_cov = np.cov(X_train_std.T) # (13, 13)
eigen_vals, eigen_vecs = np.linalg.eig(X_train_std_cov) # (13,) 、(13, 13)
draw_cum_explained_var(eigen_vals)
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))] # 把特征值和对应的特征向量组成对
eigen_pairs.sort(reverse=True) # 用特征值排序
first = eigen_pairs[0][1]
second = eigen_pairs[1][1]
first = first[:, np.newaxis]
second = second[:, np.newaxis]
W = np.hstack((first, second)) # 映射矩阵W.shape:13×2
X_train_pca = X_train_std.dot(W) # 转换训练集
draw_PCA_res(X_train_pca, y_train)
draw_PCA_res(X_test_std.dot(W), y_test)
上面我们使用了两个绘图函数,代码如下:
def draw_cum_explained_var(eigen_vals):
"""
绘制累计方差贡献率图
:param eigen_vals: numpy 特征值
:return:
"""
total = sum(eigen_vals) # 求出特征值的和
var_exp = [(i / total) for i in sorted(eigen_vals, reverse=True)] # 求出每个特征值占的比例(降序)
cum_var_exp = np.cumsum(var_exp) # 返回var_exp的累积和
plt.bar(range(len(eigen_vals)), var_exp, width=1.0, bottom=0.0, alpha=0.5, label='individual explained variance')
plt.step(range(len(eigen_vals)), cum_var_exp, where='post', label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.show()
def draw_PCA_res(data_pca, labes):
"""
绘制pca结果图
:param data_pca: pca映射后的数据
:param labes: 标签
:return:
"""
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(labes), colors, markers):
plt.scatter(data_pca[labes == l, 0], data_pca[labes == l, 1],
c=c, label=l, marker=m) # 散点图
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.show()
Fig1:累计方差贡献图

Fig2:训练数据PCA图
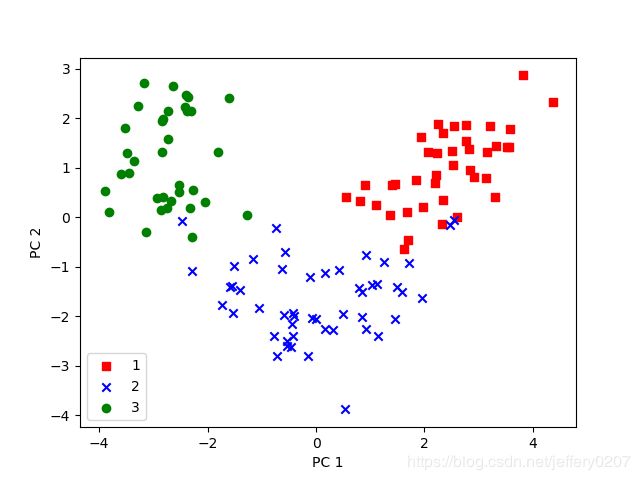
Fig3.测试集PCA图

SKlearn实例
Basic-PCA
我们先来看看在sklearn中,PCA Model 的基本属性:
from sklearn import datasets
from sklearn.decomposition import PCA
iris = datasets.load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names
pca = PCA(n_components=None)
# fit方法就相当于训练,通过训练建立有效模型
pca.fit(X)
# pca object的一些函数
# print('get_covariance', pca.get_covariance()) # 获取协方差矩阵
# print('get_precision', pca.get_precision())
# print('get_params', pca.get_params()) # 获取pca参数,于set_params对应
# print('get_score', pca.score(X)) # 平均得分
# print('get_score_samples', pca.score_samples(X)) # 得分矩阵
# pca object的一些属性
print('n_samples_: %s' % str(pca.n_samples_)) # 样本数
print('n_features_: %s' % str(pca.n_features_)) # 特征数
print('mean_: %s' % str(pca.mean_)) # 均值
print('n_components: %s' % str(pca.n_components)) # 函数调用参数的值n_components
print('n_components_: %s' % str(pca.n_components_)) # 实际n_components的值
print('explained variance ratio: %s' % str(pca.explained_variance_ratio_)) # 方差贡献率
print('explained_variance_: %s' % str(pca.explained_variance_)) # 方差贡献
# 下面的参数均来自pca = PCA(n_components=None)初始化的参数值
print('copy: %s' % str(pca.copy))
print('iterated_power: %s' % str(pca.iterated_power))
print('whiten: %s' % str(pca.whiten))
print('random_state: %s' % str(pca.random_state))
print('noise_variance_: %s' % str(pca.noise_variance_))
print('singular_values_: %s' % str(pca.singular_values_))
print('svd_solver: %s' % str(pca.svd_solver))
print('tol: %s' % str(pca.tol))
# n_samples_: 150
# n_features_: 4
# mean_: [5.84333333 3.054 3.75866667 1.19866667]
# n_components: None
# n_components_: 4
# explained variance ratio: [0.92461621 0.05301557 0.01718514 0.00518309]
# explained_variance_: [4.22484077 0.24224357 0.07852391 0.02368303]
# copy: True
# iterated_power: auto
# whiten: False
# random_state: None
# noise_variance_: 0.0
# singular_values_: [25.08986398 6.00785254 3.42053538 1.87850234]
# svd_solver: auto
# tol: 0.0
既然我们已经建立好了PCA Model,那我们继续利用Model可视化我们的pca结果:
X_r = pca.transform(X) # transform函数将数据X应用于模型,实际上就是完成了映射过程
# 绘图可视化
plt.figure()
colors = ['navy', 'turquoise', 'darkorange']
lw = 2
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=.8, lw=lw,
label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('PCA of IRIS dataset')
plt.show()
Incremental-PCA
这个PCA模式(对,我称之为模式)对熟悉深度学习的同学应该非常熟悉,就是设置一个batch-size,一个batch,一个batch来训练,为什么?因为有时候数据集很大,主机内存不够,这个时候我们就应该采取这个策略。贴一个 toy example
"""
IncrementalPCA makes it possible to implement out-of-core Principal Component Analysis either by:
1、Using its partial_fit method on chunks of data fetched sequentially from the local hard
drive or a network database.
2、Calling its fit method on a memory mapped file using numpy.memmap.
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA, IncrementalPCA
iris = load_iris()
X = iris.data
y = iris.target
n_components = 2
ipca = IncrementalPCA(n_components=n_components, batch_size=10)
X_ipca = ipca.fit_transform(X)
pca = PCA(n_components=n_components)
X_pca = pca.fit_transform(X)
colors = ['navy', 'turquoise', 'darkorange']
for X_transformed, title in [(X_ipca, "Incremental PCA"), (X_pca, "PCA")]:
plt.figure(figsize=(8, 8))
for color, i, target_name in zip(colors, [0, 1, 2], iris.target_names):
plt.scatter(X_transformed[y == i, 0], X_transformed[y == i, 1],
color=color, lw=2, label=target_name)
if "Incremental" in title:
err = np.abs(np.abs(X_pca) - np.abs(X_ipca)).mean()
plt.title(title + " of iris dataset\nMean absolute unsigned error "
"%.6f" % err)
else:
plt.title(title + " of iris dataset")
plt.legend(loc="best", shadow=False, scatterpoints=1)
plt.axis([-4, 4, -1.5, 1.5])
plt.show()
Kernel-PCA
Kernel-PCA是PCA的扩展,通过使用内核实现非线性降维,这个其实有点类似SVM,先升维再降维,它有许多应用,包括去噪,压缩和结构化预测。同样,贴一个例子
#! /usr/bin/python
# _*_ coding: utf-8 _*_
__author__ = 'Jeffery'
__date__ = '2018/11/7 16:15'
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA, KernelPCA
from sklearn.datasets import make_circles
np.random.seed(0)
X, y = make_circles(n_samples=400, factor=.3, noise=.05)
kpca = KernelPCA(kernel="rbf", fit_inverse_transform=True, gamma=10)
X_kpca = kpca.fit_transform(X)
X_back = kpca.inverse_transform(X_kpca)
pca = PCA()
X_pca = pca.fit_transform(X)
# Plot results
plt.figure()
plt.subplot(2, 2, 1, aspect='equal')
plt.title("Original space")
reds = y == 0
blues = y == 1
plt.scatter(X[reds, 0], X[reds, 1], c="red",
s=20, edgecolor='k')
plt.scatter(X[blues, 0], X[blues, 1], c="blue",
s=20, edgecolor='k')
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
# 构建平面采样点
X1, X2 = np.meshgrid(np.linspace(-1.5, 1.5, 50), np.linspace(-1.5, 1.5, 50))
X_grid = np.array([np.ravel(X1), np.ravel(X2)]).T # (2500, 2)
# 空间投射
Z_grid = kpca.transform(X_grid)[:, 1].reshape(X1.shape) # 原Z_grid.shape (2500, 393)
plt.contour(X1, X2, Z_grid, colors='grey', linewidths=1, origin='lower')
plt.subplot(2, 2, 2, aspect='equal')
plt.scatter(X_pca[reds, 0], X_pca[reds, 1], c="red",
s=20, edgecolor='k')
plt.scatter(X_pca[blues, 0], X_pca[blues, 1], c="blue",
s=20, edgecolor='k')
plt.title("Projection by PCA")
plt.xlabel("1st principal component")
plt.ylabel("2nd component")
plt.subplot(2, 2, 3, aspect='equal')
plt.scatter(X_kpca[reds, 0], X_kpca[reds, 1], c="red",
s=20, edgecolor='k')
plt.scatter(X_kpca[blues, 0], X_kpca[blues, 1], c="blue",
s=20, edgecolor='k')
plt.title("Projection by KPCA")
plt.xlabel("1st principal component in space induced by $\phi$")
plt.ylabel("2nd component")
plt.subplot(2, 2, 4, aspect='equal')
plt.scatter(X_back[reds, 0], X_back[reds, 1], c="red",
s=20, edgecolor='k')
plt.scatter(X_back[blues, 0], X_back[blues, 1], c="blue",
s=20, edgecolor='k')
plt.title("Original space after inverse transform")
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.subplots_adjust(0.02, 0.10, 0.98, 0.94, 0.04, 0.35)
plt.show()
其他
SKlearn中还实现了MiniBatchSparsePCA, SparsePCA, RandomizedPCA。
- RandomizedPCA, 这个就是朴素PCA参数中
svd_solver=randomized,我们默认是auto - SparsePCA 是朴素PCA的一个变种,处理稀疏数据,常与SparsePCACoder连用。参考06年论文:Sparse principal component analysis
- MiniBatchSparsePCA,是SparsePCA ,支持minibatch
写在篇后
在本篇中,我们介绍了PCA相关的核心数学概念、手动实现PCA,以及SKlearn中实现的PCA算法,包括PCA、IncrementalPCA、 KernelPCA、MiniBatchSparsePCA, SparsePCA, RandomizedPCA。
