UFLDL教程：数据预处理

---

数据预处理是深度学习中非常重要的一步！如果说原始数据的获得，是深度学习中最重要的一步，那么获得原始数据之后对它的预处理更是重要的一部分。
一般来说，算法的好坏一定程度上和数据是否归一化，是否白化有关。

---

数据归一化

---

数据预处理中，标准的第一步是数据归一化。虽然这里有一系列可行的方法，但是这一步通常是根据数据的具体情况而明确选择的。特征归一化常用的方法包含如下几种：

1.样本尺度归一化：简单缩放
  对数据的每一个维度的值进行重新调节，使其在 [0,1]或[-1,1] 的区间内。
  例子:在处理自然图像时，我们获得的像素值在 [0,255] 区间中，常用的处理是将这些像素值除以 255，使它们缩放到 [0,1] 中. 
2.逐样本均值消减(也称为移除直流分量)
  在每个样本上减去数据的统计平均值，用于平稳的数据（即数据每一个维度的统计都服从相同分布)，对图像一般只用在灰度图上。
3.特征标准化(使数据集中所有特征都具有零均值和单位方差) 
  首先计算每一个维度上数据的均值（使用全体数据计算），之后在每一个维度上都减去该均值，然后在数据的每一维度上除以该维度上数据的标准差。

数据尺度归一化的原因是：

(1) 数据中每个维度表示的意义不同，所以有可能导致该维度的变化范围不同，因此有必要将他们都归一化到一个固定的范围，一般情况下是归一化到[0 1]或者[-1 1]。
(2) 这种数据归一化还有一个好处是对后续的一些默认参数（比如白化操作）不需要重新过大的更改。

逐样本的均值相减

(1) 主要应用在那些具有稳定性的数据集中，也就是那些数据的每个维度间的统计性质是一样的。
比如说，在自然图片中，这样就可以减小图片中亮度对数据的影响，因为我们一般很少用到亮度这个信息。
(2) 不过逐样本的均值相减这只适用于一般的灰度图，在rgb等色彩图中，由于不同通道不具备统计性质相同性所以基本不会常用。

在数据的每个维度的统计性质是一样的时候。对于图像来说就是，对图像的照度并不感兴趣，而更多地关注其内容，这时对每个数据点移除像素的均值是有意义的，这时可以逐样本均值消减，它一般只适用于灰度图。

彩色图像不能“逐样本均值消减”，它的归一化方法及原因见 UFLDL教程: Exercise:Learning color features with Sparse Autoencoders ，即：“每一维0均值化”，进行预处理。

特征标准化

特征标准化是指对数据的每一维进行均值化和方差相等化。这在很多机器学习的算法中都非常重要，比如SVM等。

---

数据白化

---

PCA白化、ZCA白化。重点是规则化项 epsilon的选择。

数据的白化是在数据归一化之后进行的。实践证明，很多deep learning算法性能提高都要依赖于数据的白化。

在对数据进行白化前要求先对数据进行特征零均值化。这保证了
在数据白化过程中，最主要的还是参数epsilon的选择，因为这个参数的选择对deep learning的结果起着至关重要的作用。

在基于重构的模型中（比如说常见的RBM，Sparse coding, autoencoder都属于这一类，因为他们基本上都是重构输入数据），通常是选择一个适当的epsilon值使得能够对输入数据进行低通滤波。

但是何谓适当的epsilon呢？

epsilon太小，则起不到过滤效果，会引入很多噪声，而且基于重构的模型又要去拟合这些噪声
epsilon太大，则又对元素数据有过大的模糊

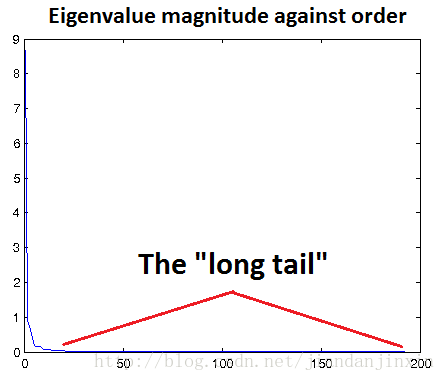
一般的方法是画出变化后数据的特征值分布图，如果那些小的特征值基本都接近0，则此时的epsilon是比较合理的。

如下图所示，让那个长长的尾巴接近于x轴。该图的横坐标表示的是第几个特征值，因为已经将数据集的特征值从大到小排序过。

---

epsilon的选择方法：

a.以图形方式画出数据的特征值
b.选取大于大多数较小的、反映数据中噪声的特征值作为 epsilon

---

实用技巧：

如果数据已被缩放到合理范围(如[0,1])，可以从epsilon = 0.01或epsilon = 0.1开始调节epsilon。

基于正交化的ICA模型中，应该保持参数epsilon尽量小，因为这类模型需要对学习到的特征做正交化，以解除不同维度之间的相关性。

---

参考文献

---

Deep learning：三十(关于数据预处理的相关技巧)

Deep Learning 11_深度学习UFLDL教程：数据预处理（斯坦福大学深度学习教程）

数据预处理