《Architecture of Convolutional Neural Networks (CNNs) demystified》,译名:卷积神经网络(CNNs)架构解密
Architecture of Convolutional Neural Networks(CNNs) demystified
卷积神经网络(CNNs)架构解密
作者:DishashreeGupta
来源:https://www.analyticsvidhya.com/
引言
曾有一段时间,我并不真正理解深度学习。我翻阅了很多相关主题的文章和研究论文,并且感觉到这是一个复杂的主题。于是,我开始试着去理解神经网络及其变体,但是这也是很困难的事情。
直到有一天,我决定从最基础的开始一步步做起,以便于能够理解分解开来的每一步是如何工作的。尽管这么做比较耗费时间与精力,但是其效果是显著的。
现在,我不仅能够理解深度学习的频谱,还能够想象到更好的运作方式,因为对于基础的清晰认识,从而能够无障碍地应用神经网络,理解其正在做什么及其背后的运作方式。
今天,我将与大家分享这一秘密,通过展示我是如何接触并掌握卷积神经网络的,以便于大家能够更好地理解CNNs的运作原理。
本文将讨论卷积神经网络的架构,其被设计用于解决图像识别和分类问题。本文适合于对于神经网络的工作原理有基础性了解的读者,否则建议先了解以下文章内容:
https://www.analyticsvidhya.com/blog/2017/05/neural-network-from-scratch-in-python-and-r/
机器是怎样看到图像的?
人脑是一台强力的精密仪器,我们能够随时捕捉各种图像并且进行处理,而且从未意识到自己正在处理这些图像。但是,机器却不行。因此,图像处理的第一步是理解,如何能够让机器合适地读懂一幅图像。
简单地讲,每幅图像都是像素点的规则排列。如果你改变像素点的位置顺序,图像也会同时发生相应的改变。举个例子,假如你想要存储并且读取一幅图像其中包含数字4的内容。
机器将会将这幅图像分解为一个像素矩阵,并且存储每个相对位置上面的像素的颜色编码。在以下的表示中,数字1代表白,数字256代表绿色的最暗阴影(为了简单,在示例中仅有一种颜色)。
一旦已经通过这种格式存储图像,下一个挑战就是使我们的神经网络理解这一排列和模式。
如何帮助神经网络识别图像?
一个数字通过某种形式的像素排列而构成。
正如我们所说的,我们尝试使用一个全连接的网络识别它。它都会做什么呢?
一个全连接网络将会把该图像分解为一个数组,通过整理图像并将像素值作为特征考虑,从而预测出图像中的数字。明显地,对于网络而言,理解底层正在发生什么是十分困难的。
即便对于人类而言,从其中识别出这是一个数字4的表达,也是不可能的。因为此时我们已经完全丢掉了像素的空间排列顺序。
我们能够做些什么呢?让我们尝试从原始图像中提取出如空间排列顺序的图像特征。
2.1 案例1
这里,我们给最初的像素值乘以一个权重值。
这样会更容易让肉眼识别出图像中有一个数字4。但是当再次将这幅图像送给一个全连接网络时,我们不得不将其拉平。这时,依旧无法保存图像的空间排列顺序。
![]()
2.2 案例2
现在我们知道,由于拉平图像导致了其排列顺序遭到完全地破坏。我们需要找到一种方法,能够在不用拉平图像并保留其空间排列顺序的情况下,将图像送给一个网络。我们需要传送像素值的二维或三维排列顺序。
让我们尝试每次取两个图像的像素值,而不是一个。这样做能够让网络了解相邻的像素排列情况。现在我们每次取两个像素,同样使用两个权重值。
希望你已经注意到这是图像由最初的4列变成了3列。由于我们每次移动两个像素(像素得到共享在每次移动中),图像变得更小了。我们将图像变得更小,并且能够在更大的程度上理解这是一个数字4。同样,需要认识到一个重要的事实,我们每次取到的是水平相邻的两个像素,因此这里仅仅考虑到水平方向的排列顺序。
这是图像特征提取方法中的一种。我们可以看到图像的左部和中部都很好,而右部不太清晰。这是因为存在以下的两个问题,
1)图像的左右边缘仅有一次乘以权重值。
2)左边权重值高,使得左部得以保留;而右边权重值低,导致右部存在明显的信息丢失。
现在我们有两个问题,同样有两种相应的解决方案。
2.3 案例3
当遇到的问题是图像左右边缘仅有一次权值相乘时,我们需要做的是让网络如同处理其它像素一样考虑边缘的像素。我们有一个简单的解决方案处理该问题,对于图像边缘进行填0扩展,以适应权重值的移动相乘。
你能够看到,通过填0操作,边缘的信息得以保留。图像的尺寸也会变大。当我们不想图像尺寸减小的时候,可以使用该办法。
2.4 案例4
现在的问题是,当右边的权值更小时,会导致像素值的降低,从而造成对于右部识别上的困难。这时,我们可以通过翻转所乘的权重值,然后组合两者的效果。
(1,0.3)权重值的输出结果为,
(0.1,5)权重值的输出结果为,
这两幅图像的组合版本将会给我们提供一个非常清晰的画面。因此,我们简单地使用乘以权重值的方法以便于保留更多的图像信息。最终的输出将是以上两幅图像的组合版本。
2.5 案例5
至此,我们已然使用权重值的方法处理了水平像素。但是,大多数情况下,还需要保留水平与垂直方向的空间排列顺序。我们可以通过一个二维的权重值矩阵来实现这一目的。同时,需要牢记,当进行水平和垂直权重值移动操作时,输出会在水平和垂直方向低一个像素。
特别感谢Jeremy Howard启发我创建了这些可视化图片。
2.6 因此我们做了什么呢?
以上内容描述了通过使用图像的空间排列顺序提取图像的特征。理解像素是如何排列的对于网络理解图像是极其重要的。
上述的操作正好是一个卷积神经网络的工作过程。通过定义一个权重值矩阵,并将其与输入图像进行卷积操作,从而提取特定的图像特征,同时还不会损失其空间排列顺序的信息。
该方法的另一个极大的好处是其降低了来自图像的参数数目。正如以上所看到的,与原始图像相比,卷积后图像的像素数目更少。这就显著地降低了所需训练的网络的参数的数量。
定义卷积神经网络
我们需要三个基本要素来构建一个基础卷积神经网络。
1)卷积层
2)池化层(可选)
3)输出层
后续我们将详细描述这三层。
3.1 卷积层
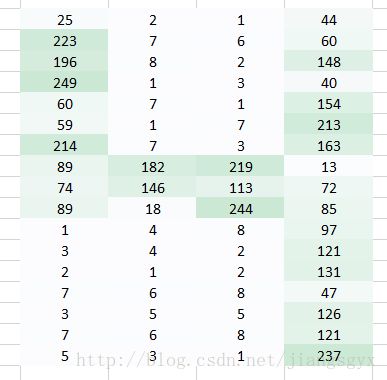
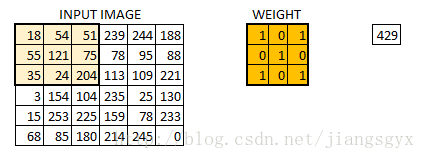
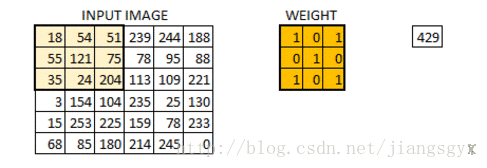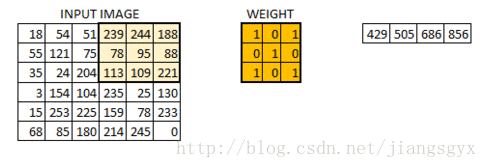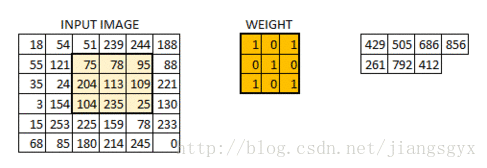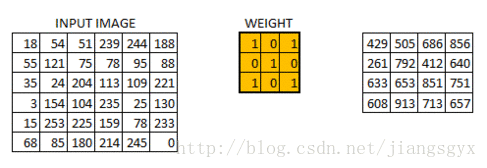
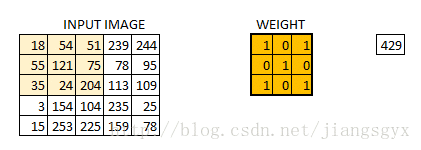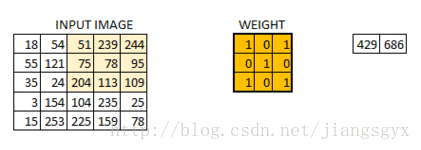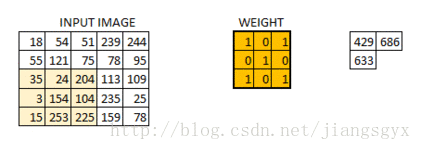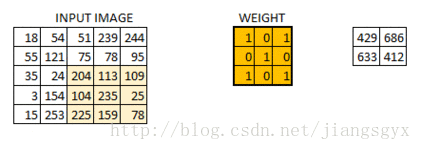
在这一层所做的工作如同上述案例5的内容。假设有一幅6*6大小的图像,我们定义一个权重值矩阵以便于提取该图像的某些特征。
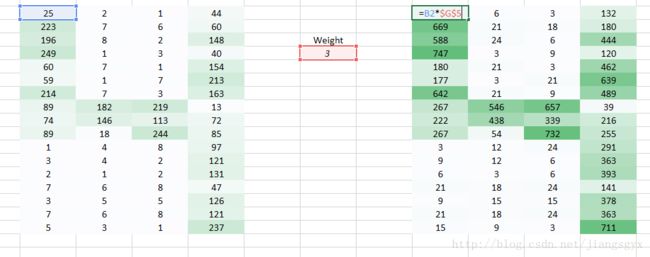
我们已经初始化了一个3*3的权重值矩阵,并且将其对图像中的每个像素进行一次运算,从而得到卷积输出。图中的429值来自于图像中相同大小(3*3)的像素区域的矩阵相乘结果。
6*6的图像在卷积后得到4*4的图像。可以想象权重值矩阵如同一个刷墙的刷子。这个刷子先沿着水平方向绘制墙面,画完一行再到下一行。当权重值矩阵在图像中移动时,像素值被重复用于计算。这基本上实现了一个卷积神经网络中的参数共享。
让我们再看一下实际图像的运算结果。
权重值矩阵想滤波器一样在一幅图像中运转,以便于从原始图像矩阵中提取特定的信息。一组权重值组合可能用于提取边缘,也有可能是提取特定的颜色,或者抹掉不想要的噪声。
类似于MLP,通过权重值学习,最小化损失的功能。因此,通过权重值学习,从能够被网络正确识别的原始图像中,提取出所需的特征内容。当我们引入卷积层时,初始层会提取到更多的通用特征,同时网络变得更深,而通过权重值矩阵所提取的特征也会越来越复杂,越来越接近实际问题的解。
3.1.1 步长和填充的概念
如上所述,滤波器或权重值矩阵,通过每次移动一个像素,对图像中的所有像素进行运算。我们可以将其定义为一个超参数,关于我们想要权重值矩阵如何在图像中进行移动。如果权重值矩阵每次移动一个像素,我们称之为1的步长。接下来让我们看一下2的步长是怎样的。
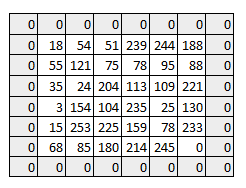
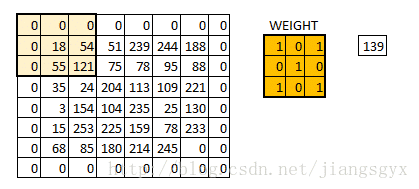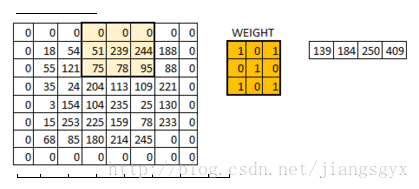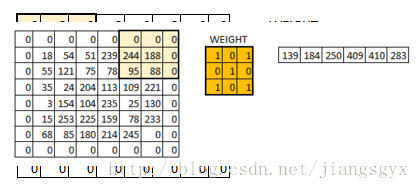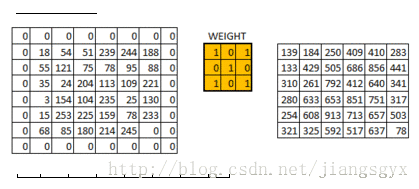
如图所示,随着步长的增加,结果图像的尺寸会减小。可以通过为输入图像填充0的方式来解决这一问题。也可以通过增加不止一层0值,以便于使用更大的步长值。
我们可以看到,在对于原始图像进行0填充后,初始的图像尺寸得以保持。这也被称为一致性填充,即输出图像具有与输入图像相同的尺寸。
一致性填充意味着我们仅仅考虑输入图像的有效像素内容。中间的4*4的像素区域应该是相同的。此时,我们保留了更多的边界信息,以及图像的尺寸。
3.1.2 多重滤波器和激活图
一种固有观念认为,权重值的深度维数应该是与输入图像的深度维数相同的。权重值扩展到输入图像的整个深度。因此,具有单一权重值矩阵的卷积也应该得到具有单一深度维度的卷积输出结果。在大多数情况下,我们使用的是具有相同维度的多重滤波器,而不是单一的滤波器(权重值矩阵)。
每个滤波器的输出被堆叠在一起形成卷积图像的深度维数。假设有一幅32*32*3的输入图像,通过有效的填充,我们对其应用10个5*5*3的滤波器,将会得到28*28*10的输出维度。
你可以想象这一过程,如下图所示。
这幅激活图是卷积层的输出结果。
3.2 池化层
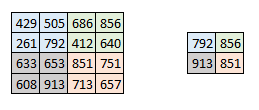
有时图像太大,我们可能需要减少训练参数的数目。然后,期望间隙地介绍后来的卷积层之间的池化层。池化的目的在于降低图像的空间尺寸。池化运算在每个深度维度上面单独进行,因此图像的深度能够保持不变。池化层最常见的应用形式是最大值池化。
此时,我们采用2的步长,池化尺寸也是2。最大值操作被应用于卷积输出的每个深度维度。如图所示,4*4的卷积输出经过最大值池化后,变为2*2大小。
让我们再看一下真实图像的最大值池化结果。
如上图所示,经过最大值池化的图像仍然保留了街道和轿车的信息。如果仔细观察,可以发现图像的维度已经变为原来的一半。这有助于在很大程度上减少学习参数。
类似地,也可以使用如平均池化或L2范数池化等其它的池化形式。
3.2.1 输出维度
对于在每个卷积层的终端理解输入与输出的维度,可能会给你造成一些混乱。我决定做一个梳理,以便于你能够更好地识别输出维度。三个超参数将会用于控制输出容量的尺寸。
1)滤波器数目——输出容量的深度将等于所应用的滤波器数目。回忆一下,我们是怎样通过堆叠每个滤波器的输出从而形成一幅激活图的。激活图的深度同样等于滤波器的数目。
2)步长——当我们使用1的步长时,每次在图像中移动一个像素的距离。随着步长加大,每次在图像中的移动距离变大,并生成更小的输出容量。
3)0填充——有助于保留输出图像的尺寸,如果使用单一的0填充,则单一滤波器作用下将会保持原始图像的尺寸。
我们可以应用一个简单的公式计算输出维度。输出图像的空间尺寸能够通过([W – F + 2P] / S) + 1计算得到。其中,W是输入容量尺寸,F是滤波器尺寸,P是填充数目,S是步长大小。假设有一幅32*32*3的输入图像,我们应用10个3*3*3的滤波器,1的步长,没有0填充。相应的W = 32,F = 3, P = 0,S = 1,输出深度应该等于所应用的滤波器的数目(10),则输出容量大小将是([32 – 3 + 0] / 1) + 1 = 30,因此输出容量将是30*30*10。
3.3 输出层
经过多层的卷积和填充后,我们需要得到某种格式的输出结果。卷积层和池化层仅仅能够从原始图像中提取特征,以及降低参数的数目。然而,想要得到最终的输出,我们需要应用一个全连接层来生成等于所需要的分类数目的输出结果。得到对应于卷积层的数目是困难的。由于卷积层生成三维的激活图,而我们只是需要一幅图像是否属于某个特殊分类的输出结果。输出层具有类似于绝对互熵的损耗功能,以计算预测误差。一旦前向传递完成,则反馈过程开始更新权重值和偏差,以降低误差和损耗。
把所有的放到一起——完整的网络看起来怎么样?
如上所述,CNN是由多个卷积和池化层所组成的,如下图所示。
向第一级卷积层传入输入图像,卷积输出一幅激活图。卷积层滤波器从输入图像中提取到有关特征并向后传递。
每个滤波器都会提供一个不同的特征用于正确的分类识别。如果需要保留图像尺寸,可以使用一致性填充(0填充),其它的有效填充也会用到,以降低特征数目。
引入池化层以便于进一步降低参数的数目。
在识别之前,具有多个卷积层和池化层,卷积层用于提取特征,当网络越深,就有越多的指定特征被提取,而浅的网络所提取的特征则是更一般的。
CNN的输出层,如先前所述,是一个全连接层,来自其它层的输入被转换和传输,以便于通过网络得到期望的分类输出。
输出结果是由输出层通过误差比对所生成的。一个损耗功能被定义在全连接输出层中以计算均方损耗,并计算出误差梯度。
然后通过误差反馈更新滤波器(权重值)和偏差值。
在一个单独的向前和向后的通路完成后,一次训练周期结束。
在KERAS使用CNN分类图像
接下来做个实验,通过输入多张含有猫狗内容的图像,然后依据各自的动物范畴对这些图片进行分类。这属于图像识别与分类领域的经典问题。机器需要做的是通过多种特征看见并理解这些图像,从而分辨出图像中是猫还是狗。
所需的特征可能类似于提取边缘,或者提取猫的胡须等等。卷积层将会提取这些特征。让我们建立一个数据集,如下图所示的一些数据集中的图片实例。
首先,我们需要将这些图像变换为相同的尺寸,通常在获取图像时,不可能确保每张图像都具有相同的尺寸。
为了便于理解,我仅使用了单一的卷积层和单一的池化层,通常进行预测的时候不会有这种情况发生。
#import various packages
import os
import numpy as np
import pandas as pd
import scipy
import sklearn
import keras
from keras.models import Sequential
import cv2
from skimage import io
%matplotlib inline#Defining the File Path
cat=os.listdir("/mnt/hdd/datasets/dogs_cats/train/cat")
dog=os.listdir("/mnt/hdd/datasets/dogs_cats/train/dog")
filepath="/mnt/hdd/datasets/dogs_cats/train/cat/"
filepath2="/mnt/hdd/datasets/dogs_cats/train/dog/"
#Loading the Images
images=[]
label = []
for i in cat:
image = scipy.misc.imread(filepath+i)
images.append(image)
label.append(0) #for cat images
for i in dog:
image = scipy.misc.imread(filepath2+i)
images.append(image)
label.append(1) #for dog images
#resizing all the images
for i in range(0,23000):
images[i]=cv2.resize(images[i],(300,300))
#converting images to arrays
images=np.array(images)
label=np.array(label)
# Defining the hyperparameters
filters=10
filtersize=(5,5)
epochs =5
batchsize=128
input_shape=(300,300,3)
#Converting the target variable to the required size
from keras.utils.np_utils import to_categorical
label = to_categorical(label)
#Defining the model
model = Sequential()
model.add(keras.layers.InputLayer(input_shape=input_shape))
model.add(keras.layers.convolutional.Conv2D(filters, filtersize, strides=(1, 1), padding='valid', data_format="channels_last", activation='relu'))
model.add(keras.layers.MaxPooling2D(pool_size=(2, 2)))
model.add(keras.layers.Flatten())
model.add(keras.layers.Dense(units=2, input_dim=50,activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(images, label, epochs=epochs, batch_size=batchsize,validation_split=0.3)
model.summary()在这一模型中,仅仅用到了单一卷积和池化层,训练参数为219801个。想象一下,如果使用MLP,将会有多少个参数。后续可以通过增加更多的卷积和池化层来减少参数数目。我们所增加的特征提取卷积层越多,所获取的特征也就越明确越复杂。