二叉堆
二叉堆是数据结构中优先队列的一种实现。二叉堆具有两个性质:结构性和堆序性。
1、结构性
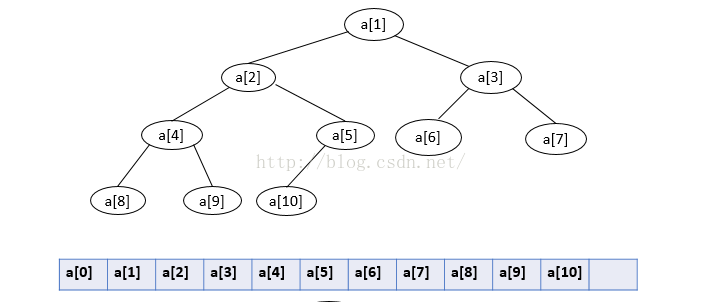
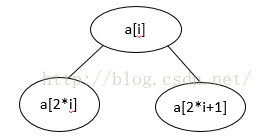
二叉堆其实就是一棵完全二叉树。除了最底层之外,其余层都被完全填充。这个完全二叉树可以不使用指针,而使用数组来表示,其中a[0]的位置存储的是一个标记(sentinel),对于最小二叉堆a[0] = MinData,有了这个标记编程是很方便的,当然也可以不使用这个标记。
2、堆序性
《数据结构与算法分析:C语言描述》是这样定义堆序性的:使操作被快速执行的性质叫做堆序性。比如对于最小二叉堆(一种优先队列的实现),我们希望可以优先(快速)的找到二叉堆中最小的元素。如果最小二叉堆的最小元素始终在根的位置,那么我们就可以每次以常数时间找到最小元素。所以最小二叉堆的堆序性就是任意一个父节点中的键值总是小于或等于子节点中的键值。同样最大二叉堆具有类似的堆序性。
3、二叉堆的基本操作:Insert()和DeleteMin()
二叉堆作为优先序列的一种实现,至少有出列 DeleteMin( ) 和入列 Insert( )两种基本操作,但无论哪操作二叉堆都要始终保持结构和堆序性。
先看下二叉堆的结构体的声明:
struct HeapStruct
{
int Capacity; /* 二叉堆的最大元素数量,即数组的大小减去1 */
int Size; /* 指示用于创建二叉堆的元素的数量,即二叉堆的大小 */
ElementType *Elements; /* 指向数组的指针 */
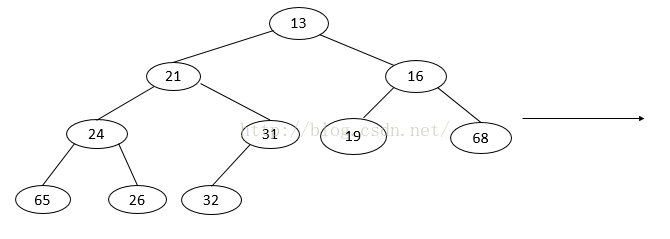
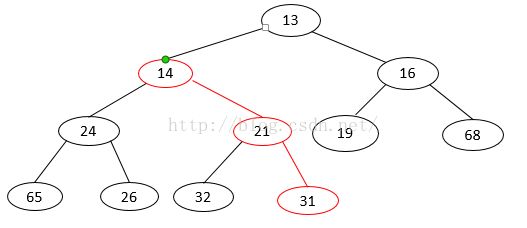
};第(3)步:继续把新元素14与空穴的父节点里的元素比较,重复第三步,直到14小于空穴的父节点里的元素值时停止。
第(4)步:将新元素放入空穴。下面右侧图中是最终的插入结果,红色代表上虑的路径。
void Insert(ElementType X, PriorityQueue H)
{
int i;
if (IsFull(H))
{
printf("优先队列已满\n");
return;
}
/* 上虑一层,因为在Elements[0] 添加了一个标记 MinData,故不再判断 i>0 */
for (i=++H->Size; H->Elements[i/2]>X; i /= 2)
H->Elements[i] = H->Elements[i/2];
H->Elements[i] = X;
}3.2、删除最小元 DeleteMin()
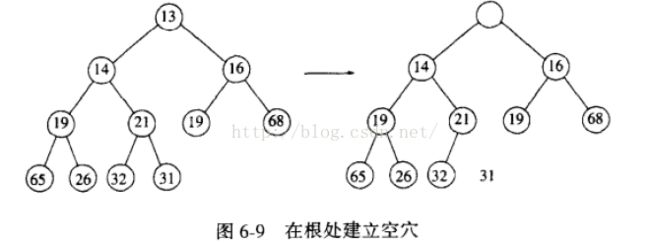
删除最小元我们采用下虑(percolate down)的策略,就是把空穴从上层往下层一层层下虑。对于最小二叉堆,最小元就位于树的根处,找到很容易,但删除之后在树的根处会留下一个空穴。继续用上面的堆作为例子(画图太累了,直接盗图)。
第(1)步:取出根部元素,留下一个空穴在根处。同时取出最底层最右侧的元素(也就是数组中构成二叉树的最后一个元素放入临时变量temp中,将Size减1。其实删除的位置在树的最后一片树叶上。
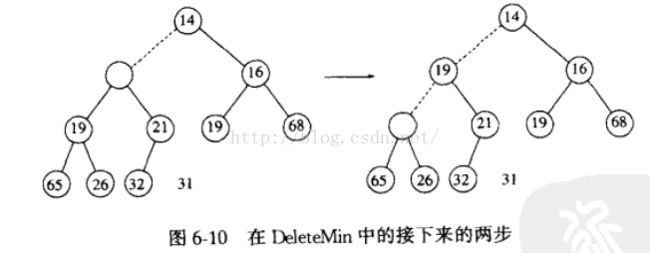
第(2)步:比较空穴的两个子节点中的元素,取出较小的元素。
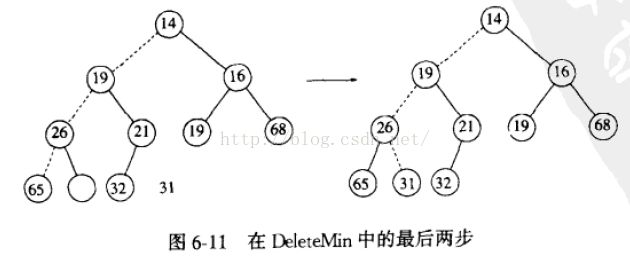
第(3)步:若较小元素不大于temp,则将较小元素放入空穴, 此时在新的位置产生新的空穴,重复(2)。若较小元素大于temp,则直接将temp放入空穴。
DeleteMin()代码如下:
ElementType DeleteMin(PriorityQueue H)
{
int i, Child;
ElementType MinElement; /* 返回的值 */
ElementType LastElement;
if (IsEmpty(H))
{
printf("队列已为空\n");
return;
}
MinElement = H->Elements[1];
/* 取出最后一个元素,用于填充下虑完成后剩余的一个空穴 */
LastElement = H->Elements[H->Size--];
for (i=1; i<=H->Size; i=Child)
{
Child = 2 * i;
/* Child != H->Size 说明第 i 个结点有两个子节点,用了一个技巧省去了对是否存在两个子节点的判断; 并且让Child处是较小的一个儿子 */
if (Child!=H->Size&&H->Elements[Child+1]Elements[Child])
Child++;
/* 下虑一层 */
if (LastElement > H->Elements[Child])
H->Elements[i] = H->Elements[Child];
else
break;
}
H->Elements[i] = LastElement; /* 填充最后的一个空穴 */
return MinElement;
} 4.1 降低某一位置键值的值
/**
* 减小位置P处的键值
* 由于P处键值减小了,破坏了堆的序
* 可以通过上虑来调整; 类似于 Insert()
*/
void DecreaseKey(Position P, ElementType Decrement, PriorityQueue H)
{
int i;
ElementType temp;
H->Elements[P] -= Decrement;
temp = H->Elements[P];
//上虑调整
//由于数组的起始位置存储了一个最小的元素,所以也可以不用判断i>0
for (i = P; i>0 && H->Elements[i/2]>temp; i /= 2)
H->Elements[i] = H->Elements[i/2];
H->Elements[i] = temp;
}
4.2 、增加某一位置键值的值
/**
* 增大位置P处的键值
* 由于P处键值增大了,破坏了堆的序
* 可以通过下虑来调整; 类似于 DeleteMin()
*/
void IncreaseKey(Position P, ElementType Increment, PriorityQueue H)
{
int i;
ElementType temp;
H->Elements[P] += Increment;
temp = H->Elements[P];
/* 下虑调整 */
for (i=2*P; i<=H->Size; i*=2)
{
if (i!=H->Size&&H->Elements[i]>H->Elements[i+1])
i++;
if (temp > H->Elements[i])
H->Elements[i/2] = H->Elements[i];
else
break;
}
H->Elements[i/2] = temp;
}
/**
* 把N个键值存放入二叉堆中
* 方法:(1)可以通过N次的Insert()来实现;
* (2)也可以先把N个键值直接存入队列后,再通过下虑重建堆
*/
void MultiInsertHeap(ElementType Elements[], int N, PriorityQueue H)
{
int i;
int Child;
ElementType temp;
if ((H->Size+N) > H-> Capacity)
return;
for (i = 0; iElements[++H->Size] = Elements[i];
}
/* 下虑调整 */
for (i=H->Size/2; i>0; i--)
{
Child = 2*i;
if (Child!=N&&H->Elements[Child]>H->Elements[Child+1])
Child++;
if (H->Elements[i]>H->Elements[Child])
{
temp = H->Elements[i];
H->Elements[i] = H->Elements[Child];
H->Elements[Child] = temp;
}
}
}
/* 优先队列的初始化(创建) */
PriorityQueue Initialize(int MaxElements)
{
PriorityQueue H;
//ElementType MinData = 0;
if (MaxElements < MinPQSize)
{
printf("MaxElements 小于允许的最小优先队列大小\n");
return;
}
H = malloc(sizeof(struct HeapStruct));
if (H==NULL)
{
printf("申请优先队列结构空间失败\n");
return;
}
/* 申请的数组大小是MaxElements+1,额外的一个用于存储标记,放置于数组的第一个元素*/
H->Elements = malloc((MaxElements+1)*sizeof(ElementType));
if (H->Elements==NULL)
{
printf("申请数组空间失败\n");
return;
}
H->Capacity = MaxElements;
H->Size = 0;
H->Elements[0] = MinData; // 额外申请的一个空间存放MinData
return H;
}参考:《数据结构与算法分析:C语言描述》
《数据结构基础(C语言版)》