中心极限法则是统计学中的一个定则,内容很简单:一个随机变量,不管是什么分布,当其样本足够大时,其均值不是原来的分布,而是自然分布。所以并不是原来的变量的分布改变了,其实并没有变,只是他的均值满足自然分布而已。
假设有一个长为3的时间序列,每个时间点都是一个随机变量,第一个满足指数分布,第二个满足均值分布,第三个满足二项式分布。我们通过Matlab来获取满足假设的时间序列:
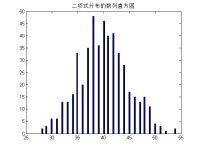
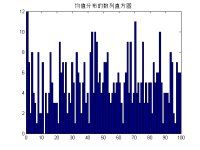
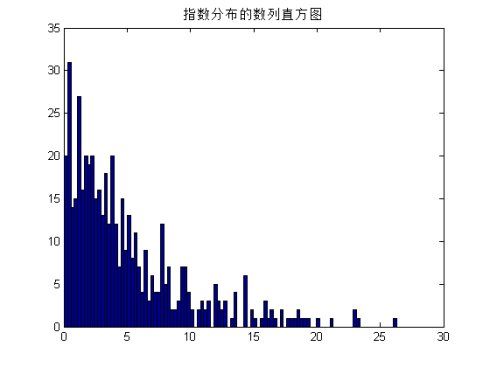
通过help random来查看对应分布的表示,于是我们将选择bino,exp和unif这三个分布并设置其对应的参数,从而产生的序列为1*500(不是时间序列),通过直方图显示我们观察到这三个序列的分布的确满足给定的分布。
x1=random('exp',5,1,500);
x2=random('bino',100,0.4,1,500);
x3=random('unif',0,100,1,500);
现在我们运用中心极限定则求自然分布:
1.1.首先利用分布函数产生一个1*500的序列,这个序列为二项式分布、指数分布或者均值分布;
2.2.求序列的均值m,这相当于均值的一个样本;
3.3.重复1.2步骤,求得一个均值的数列,我们假定要求10000个这样的均值,重复10000次;
4.4.求出均值的直方图
fori=1:1:10000%3.重复1.2步骤10000次
x1=random('exp',5,1,500);%1.求指数分布序列1*500
m1(i)=mean(x1);%2.求序列的均值
end
figure,hist(m1,500)%4.求获得的10000个均值的分布
title('指数分布数列的均值分布直方图');
fori=1:1:10000%3.重复1.2步骤10000次
x2=random('bino',100,0.4,1,500);%1.求指数分布序列1*500
m2(i)=mean(x2);%2.求序列的均值
end
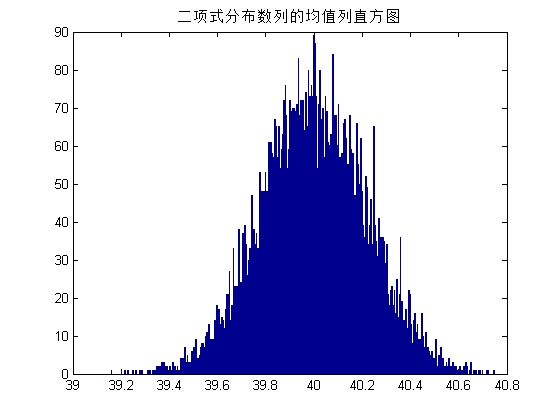
figuere,hist(m2,500)%4.求获得的10000个均值的分布
title('二项式分布数列的均值列直方图');
fori=1:1:10000%3.重复1.2步骤10000次
x3=random('unif',0,100,1,500);%1.求指数分布序列1*500
m3(i)=mean(x3);%2.求序列的均值
end
figure,hist(m3,500)%4.求获得的10000个均值的分布
title('均值分布数列的均值的直方图');
结果然如预期,他们的分布都接近于自然分布!