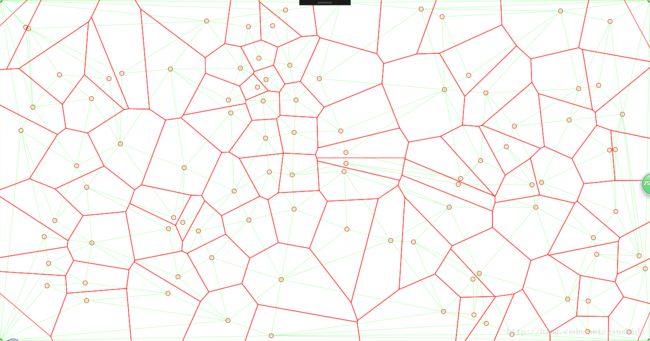
生成泰森多边形
void ConvexHull(Point[] pts)
{
int[][] temp = new int[pts.Length][];
for (int i = 0; i < pts.Length; i++)
{
temp[i] = new int[2];
temp[i][0] = (int)(pts[i].X + pts[i].Y);
temp[i][1] = (int)(pts[i].X - pts[i].Y);
}
List ls = temp.ToList();
int max1index = ls.FindIndex(o => o[0] == ls.Max(j => j[0]));
int max2index = ls.FindIndex(o => o[1] == ls.Max(j => j[1]));
int min1index = ls.FindIndex(o => o[0] == ls.Min(j => j[0]));
int min2index = ls.FindIndex(o => o[1] == ls.Min(j => j[1]));
Console.Write(string.Format("{0},{1},{2},{3}", max1index, min1index, max2index, min2index));
//找出点集中,最靠近点集四至的点。为了简化操作,我将点集pts的四至角点都加入了点集中,避免了外围凸包的复杂度和Voronoi切分时考虑边界
List tubao = new List();
List other = new List();
//根据最右原则,求取凸包点列表。如果像我之前将四至角点加入点集,这部分可以除去,直接构建凸包点列表
Point Pi, Pj, Pk;
int st = max1index, ed = max2index;
Pk = pts[st];
Pi = Pk;
Pj = pts[ed];
do
{
if (tubao.Count > 0)
Pj = Pk;
con:
bool right = false;
List rightpt = new List();
rightpt.Clear();
for (int i = 0; i < pts.Length; i++)
{
if (pts[i].Equals(Pi)) continue;
if (pts[i].Equals(Pj)) continue;
int re = getPtDirection(Pi, Pj, pts[i]);
if (re > 0)
{
right = true;
rightpt.Add(pts[i]);
}
else if (re == 0)
{
//共线
right = false;
}
else
{
right = false;
}
}
if (rightpt.Count == 0)
{
//更改后继点
tubao.Add(Pi);
Pi = Pj;
continue;
}
else
{
List rlen = new List(rightpt.Count);
foreach (var pt in rightpt)
{
rlen.Add(pt2lnDis(pt, Pi, Pj));
}
int index = rlen.FindIndex(o => o == rlen.Max());
Pj = rightpt[index];
goto con;
}
}
while (tubao.Count == 1 || !tubao[tubao.Count - 1].Equals(tubao[0]));
//列表中首尾点一致,去除首点或尾点,我这里去除了首点
tubao.RemoveAt(0);
//求取内含点列表
foreach (var pt in pts)
{
if (tubao.Contains(pt))
{ }
else
other.Add(pt);
}
//记录凸包点数量
int duanPtcount = tubao.Count;
//三角形集合
Dictionary dic = new Dictionary();
List tubaocopy = new List();
for (int i = 0; i < tubao.Count; i++)
{
tubaocopy.Add(i);
}
//凸包切分,凸包临边构成三角形内不含其它凸包点
while (tubaocopy.Count > 3)
{
int fh = 0;
for (int i = 0; i < tubaocopy.Count - 1; i++)
{
bool allcheck = false;
triangle tr = new triangle() { p1 = i == 0 ? tubao[tubaocopy[tubaocopy.Count - 1]] : tubao[tubaocopy[i - 1]], p2 = tubao[tubaocopy[i]], p3 = i == tubaocopy.Count - 1 ? tubao[tubaocopy[0]] : tubao[tubaocopy[i + 1]] };
for (int dex = 0; dex < i - 1; dex++)
{
allcheck = inTri(tr, tubao[tubaocopy[dex]]);
if (allcheck) break;
}
for (int dex = i + 1; allcheck && dex < tubaocopy.Count; dex++)
{
allcheck = inTri(tr, tubao[tubaocopy[dex]]);
if (allcheck) break;
}
if (allcheck) continue;
fh = i;
dic.Add(FormatIndex( i == 0 ? tubaocopy[tubaocopy.Count - 1] : tubaocopy[i - 1], tubaocopy[i], i == tubaocopy.Count - 1 ? tubaocopy[0] : tubaocopy[i + 1]), tr);
break;
}
tubaocopy.RemoveAt(fh);
}
dic.Add(FormatIndex(tubaocopy[0],tubaocopy[1],tubaocopy[2]), new triangle() { p1 = tubao[tubaocopy[0]], p2 = tubao[tubaocopy[1]], p3 = tubao[tubaocopy[2]] });
//内含点进行内插
for (int i = other.Count - 1; i >= 0; i--)
{
Point tp = other[i];
List ts = new List();
foreach (var key in dic.Keys)
{
if (inTri(dic[key], tp))
{
ts.Add(key);
}
}
tubao.Add(tp);
int pindex = tubao.Count - 1;
//点在三角形内或在单边上
if (ts.Count == 1)
{
foreach (var t in ts)
{
dic.Remove(t);
int[] old = getIndex(t).ToArray();
triangle tr;
string ky = string.Empty;
List tmp;
Point otpt;
tr = new triangle() { p1 = tubao[old[0]], p2 = tubao[old[1]], p3 = tubao[pindex] };
InTriCheck(tr,ref dic,ref tubao,old[0],old[1],pindex);
tr = new triangle() { p1 = tubao[old[0]], p2 = tubao[old[2]], p3 = tubao[pindex] };
InTriCheck(tr, ref dic, ref tubao, old[0], old[2], pindex);
tr = new triangle() { p1 = tubao[old[2]], p2 = tubao[old[1]], p3 = tubao[pindex] };
InTriCheck(tr, ref dic, ref tubao, old[2], old[1], pindex);
}
}
//点在三角形边共边(没有重复点)
else if (ts.Count > 1)
{
List> gx = ts.Select(o => getIndex(o)).ToList();
IEnumerable en = null;
IEnumerable all = null;
foreach (var g in gx)
{
if (en == null) { en = g.Take(g.Count);all=g.Take(g.Count) ; continue; }
en = g.Take(g.Count).Intersect(en);
all=all.Union(g.Take(g.Count));
}
int[] re = en.ToArray();
if (re.Length > 0)
{
if (re.Length == 1)
{ }
else if (re.Length == 2)
{
for (int g = 0; g < re.Length; g++)
{
int op = gx[g].Take(gx[g].Count).Except(re.Take(2)).ToArray()[0];
dic.Remove(ts[g]);
dic.Add(FormatIndex(op, re[0], pindex), new triangle() { p1 = tubao[op], p2 = tubao[re[0]], p3 = tubao[pindex] });
dic.Add(FormatIndex(op, re[1], pindex), new triangle() { p1 = tubao[op], p2 = tubao[re[1]], p3 = tubao[pindex] });
}
}
else
{
}
}
else
{ }
}
}
//顺序连接内含点所对应的三角形外心,获得泰森多边形边界。
//由于我对点集做了处理,加入了四至角点,所以凸包必为四至图形,只需对内插点(也就是非四至角点)进行处理即可
//如果此处是使用的凸包,还需要对凸包点再继续处理
List Voronoi=new List();
for (int i=duanPtcount;i kys=dic.Keys.ToList().FindAll(o=>o.Contains(string.Format("-{0}-",i)));
if (kys.Count == 0) continue;
List ptorder = kys.Select(o=>o.Replace("-"+i +"-","-")).ToList();
string apt = ptorder[0];
ptorder.Remove(apt);
while (ptorder.Count>0)
{
string fontOrder = apt.Substring(0,apt.Trim('-').IndexOf("-")+2);
string nextfont=ptorder.Find(o=>o.Contains(fontOrder));
ptorder.Remove(nextfont);
nextfont = nextfont.Replace(fontOrder, "").Trim('-');
apt = string.Format("-{0}{1}",nextfont,apt);
}
List lt = new List();
Polygon pgon = new Polygon();
List indexs = getIndex(apt);
for (int n=0;no.Contains("-"+indexs[n]+"-")&& o.Contains("-" + indexs[n+1] + "-"));
pgon.Points.Add(dic[sky].Center);
}
pgon.Stroke = new SolidColorBrush() { Color=Colors.Red};
Voronoi.Add(pgon);
}
}
//判断点在三角形内,在边界上的点认为在内
public bool inTri(triangle tr, Point p)
{
int r1 = getPtDirection(p, tr.p1, tr.p2);
int r2 = getPtDirection(p, tr.p1, tr.p3);
if (r1 == 0)
{
if (p.X < Math.Max(tr.p1.X, tr.p2.X) && p.X > Math.Min(tr.p1.X, tr.p2.X) &&
p.Y < Math.Max(tr.p1.Y, tr.p2.Y) && p.Y > Math.Min(tr.p1.Y, tr.p2.Y))
return true;
else
return false;
}
if (r2 == 0)
{
if (p.X < Math.Max(tr.p1.X, tr.p3.X) && p.X > Math.Min(tr.p1.X, tr.p3.X) &&
p.Y < Math.Max(tr.p1.Y, tr.p3.Y) && p.Y > Math.Min(tr.p1.Y, tr.p3.Y))
return true;
else
return false;
}
if (r1 == r2)
return false;
r1 = getPtDirection(p, tr.p2, tr.p1);
r2 = getPtDirection(p, tr.p2, tr.p3);
if (r1 == 0)
{
if (p.X < Math.Max(tr.p1.X, tr.p2.X) && p.X > Math.Min(tr.p1.X, tr.p2.X) &&
p.Y < Math.Max(tr.p1.Y, tr.p2.Y) && p.Y > Math.Min(tr.p1.Y, tr.p2.Y))
return true;
else
return false;
}
if (r2 == 0)
{
if (p.X < Math.Max(tr.p2.X, tr.p3.X) && p.X > Math.Min(tr.p2.X, tr.p3.X) &&
p.Y < Math.Max(tr.p2.Y, tr.p3.Y) && p.Y > Math.Min(tr.p2.Y, tr.p3.Y))
return true;
else
return false;
}
if (r1 == r2)
return false;
return true;
}
//插入三角形后,对后续三角形进行外心判断,并调整
private bool InTriCheck(triangle tr, ref Dictionary dic,ref List tubao, int v1, int v2, int pindex)
{
try
{
string ky = string.Empty;
List tmp;
ky = dic.Keys.FirstOrDefault(o => o.Contains("-" + v1.ToString() + "-") && o.Contains("-" + v2.ToString() + "-"));
if (!string.IsNullOrEmpty(ky))
{
tmp = getIndex(ky);
tmp.Remove(v1);
tmp.Remove(v2);
Point otpt = tubao[tmp[0]];//对角点
if (tr.radius > getLenFromP2(tr.Center, otpt))
{
dic.Remove(ky);
InTriCheck(new triangle() { p1 = tubao[v1], p2 = tubao[tmp[0]], p3 = tubao[pindex] }, ref dic, ref tubao, v1, tmp[0], pindex);
InTriCheck(new triangle() { p1 = tubao[v2], p2 = tubao[tmp[0]], p3 = tubao[pindex] }, ref dic, ref tubao, v2, tmp[0], pindex);
return false;
}
else
{
dic.Add(FormatIndex(v1, v2, pindex), tr);
return true;
}
}
else
{
dic.Add(FormatIndex(v1, v2, pindex), tr);
return true;
}
}
catch { dic.Add(FormatIndex(v1, v2, pindex), tr);return true; }
} 其他方法的一些说明
getIndex:对于三角形,我是采用的"点1编号-点2编号-点3编号"的形式来作为键值,该方法是键值到点编号的转换。
FormatIndex:形成键值。
getLenFromP2:计算两点间距离。
getPtDirection:一点在另两点形成的矢量的左侧、右侧或线上。我这个方法大于零为右侧。
算法思路参考 http://blog.csdn.net/gdut2015go/article/details/48208983
示例图(红色圈为输入点,另外我还加入了四至角点,绿色为三角网,红色线为泰森多边形)