单目标跟踪——个人笔记

单目标跟踪——个人笔记

以《Handcrafted and Deep Trackers: A Review of Recent ObjectTracking Approaches》为主线看单目标跟踪文献。
不会完全相同，会根据自己看文献和做实验的情况决定顺序与内容。
随手记，不定期更。

MOSSE

D. S. Bolme, J. R. Beveridge, B. A. Draper, and Y. M. Lui, “Visual object tracking using adaptive correlation filters,” in CVPR. IEEE, 2010.
是在线相关滤波跟踪的鼻祖吧，前身为ASEF(offline)。很简单，就是一个岭回归。

CSK与KCF

J. F. Henriques, R. Caseiro, P. Martins, and J. Batista, “Exploiting the circulant structure of tracking-by-detection with kernels,” in ECCV. Springer, 2012, pp. 702–715.
João F. Henriques, Rui Caseiro, Pedro Martins, Jorge Batista, “High-speed tracking with kernelized correlation filters,” IEEE T-PAMI, vol. 37, no. 3, pp. 583–596, 2015
贴两篇个人认为比较详细的介绍就好1CSDN、2知乎，还有一个KCF弊端与解决方法的博客
总结一下KCF的 缺点 :

• 1.单一尺度；
• 2.学习率固定：学习率过大会导致目标遮挡时过度学习背景信息，学习率过小会导致目标快速变形时滤波器更新不及时丢失目标；(如何更新，世界难题啊)
• 3.边界效应，即循环移位得到的样本不是真实样本，这会限制训练得到的滤波器的判别能力；
• 4.对快速运动目标跟踪效果差，因为加了余弦窗弱化边界上的信息，如果相邻帧中的目标平移较大，导致目标到了边界区域，此时余弦窗会弱化目标信息，导致跟踪效果不理想；
• 5.要求目标的patch size和滤波器的大小必须一致，因此对不规则、轮廓形状变化大的目标不友好。

HCF与HCFT*

C. Ma, J. B. Huang, X. Yang, and M. Yang, “Hierarchical convolutional features for visual tracking,” in ICCV. IEEE, 2015, pp. 3074–3082.
C. Ma, J. Huang, X. Yang, and M. Yang, “Robust visual tracking via hierarchical convolutional features,” IEEE T-PAMI, 2018.

HCF

利用VGGNet-19提取深度特征，并选取conv3-4、conv4-4和conv5-4三层的特征(大小为[37，28，19])，并通过双线性插值将三层特征图调整至同一大小，然后分别对每层特征图做相关滤波操作，最后加权融合(权重为[1，0.5，0.02])三层特征对应的置信度图，得到最终的置信度图。

HCFT*

增加了尺度估计和重捕功能。【待看】

HDT

Y. Qi, S. Zhang, L. Qin, H. Yao, Q. Huang, J. Lim, and M. Yang, “Hedged deep tracking,” in CVPR. IEEE, 2016, pp. 4303–4311

HDT使用了六层VGGNet的特征图，并分别对每一层特征图训练一个相关滤波器(弱跟踪器)，并将所有弱分类器通过Hedge algorithm进行结合，得到一个强跟踪器，最终输出结果。
相对于HCF，加权的权重是自适应的，即在线学习得到的。
18年又发了一篇到TPAMI上Hedging Deep Features for Visual Tracking。【待看】

SAMF

Y. Li and J. Zhu, “A scale adaptive kernel correlation filter tracker with feature integration,” in ECCV. Springer, 2014, pp. 254–265.

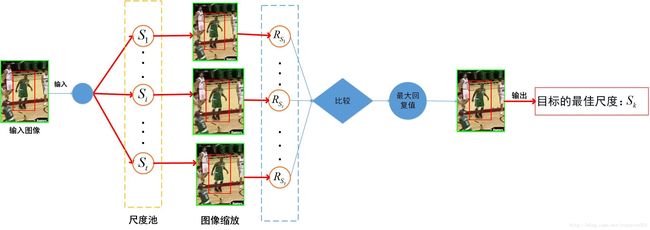
为了解决尺度问题，加入了尺度金字塔，总共7个尺度[0.985, 0.99, 0.995, 1.0, 1.005, 1.01, 1.015]，此为SA。
为了提高精度，使用了多特征，HOG+CN+灰度，此为MF。
速度还是比较慢的，2、30帧吧。

DSST与fDSST

M. Danelljan, F. Shahbaz Khan, M. Felsberg, and J. van de Weijer, “Adaptive color attributes for real-time visual tracking,” in BMVC, 2014.
M. Danelljan, G. Hager, F. S. Khan, and M. Felsberg, “Discriminative scale space tracking,” IEEE T-PAMI, vol. 39, pp. 1561–1575, 2017
官网主页
一样是为了解决尺度问题。
DSST 思路很简单，将跟踪分为平移(位置)预测和尺度预测两部分，先在当前帧上做平移预测，得到目标在当前帧的位置，再以当前帧预测得到目标位置为中心，做尺度预测(尺度金字塔，共有33个尺度)。平移滤波器和尺度滤波器是独立的两个滤波器，且都是基于MOSSE实现的。
fDSST 则是对DSST速度上的优化，首先尺度数改为17个，并通过三角插值的方法将17个尺度插值成33个尺度。然后在对特征维度(HOG:1维灰度+31维fHOG)做PCA降维(降维后只有18维)，为了提速，通过QR分解实现PCA降维。另外，为了做到像素级别精度，31维fHOG会做插值，插值到灰度图像大小。
实测速度 从DSST的4、50帧提速到了8、90帧(i5-7300HQ笔记本，具体和目标初始大小以及CPU有关)，官方宣称的提速比例差不多。
缺点 ：很容易丢，即这算法对平移预测精度要求很高，否则容易陷入局部最优造成目标丢失。
与SAMF具体的对比见这篇博客。

LCT与ILCT

C. Ma, X. Yang, C. Zhang, and M. Yang, “Long-term correlation tracking,” in CVPR. IEEE, 2015, pp. 5388–5396
C. Ma, J.-B. Huang, X. Yang, and M.-H. Yang, “Adaptive correlation filters with long-term and short-term memory for object tracking,” IJCV, pp. 1–26, 2018.

KCF用于长时跟踪的文章，说到长时跟踪就顺便推荐一下这篇Z. Kalal, K. Mikolajczyk, and J. Matas. Tracking-Learning-Detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 34(7):1409–1422, 2012.
LCT 跟踪部分与DSST类似，都是独立的平移预测R_c+独立的尺度预测R_s(利用了时空上下文信息)。在此基础上，LCT还增加了第三个负责检测目标置信度的相关滤波器R_t，其不利用了时时间上下文信息，只选取靠谱帧的信息，没有padding，也不加余弦窗。跟踪顺序：先利用R_c检测平移结果y_c，并用R_t根据y_c重新检测置信度，然后根据y_c建立尺度金字塔，用R_s检测，选取置信度最大的尺度作为下一帧尺度。更新方式：对于R_c和R_s每帧进行跟新，对于R_t，只有当目标位置置信度大于设定的阈值T_appearance(0.38)时才进行跟新，都是固定学习率更新。除此之外，LCT多了重检测(re-detection) 的功能，即当预测的目标位置置信度(R_t检测得到的)低于设定的阈值T_motion(0.15)时，LCT将进入重检测步骤。LCT中的重检测通过在线的随机阙分类器(online random fern classifier)实现。
ILCT 则将随机阙分类器换成了SVM。【待看】

MCPF

T. Zhang, C. Xu, and M. Yang, “Multi-task correlation particle filter for robust object tracking,” in CVPR. IEEE, July 2017, pp. 4819–4827.
多任务相关滤波+粒子滤波__【待看】__

STAPLE

L. Bertinetto, J. Valmadre, S. Golodetz, O. Miksik, and P. Torr, “Staple: Complementary Learners for Real-Time Tracking,” in CVPR. IEEE, 2016.

未完成

CREST

Y. Song, C. Ma, L. Gong, J. Zhang, R. Lau, and M. Yang, “CREST: Convolutional Residual Learning for Visual Tracking,” in ICCV. IEEE, 2017


将传统的相关滤波重构成单层卷积形式的端对端的跟踪方法(将特征提取和响应图生成融合到了一起)，同时为了减少在线更新时的模型退化，在计算响应图时引入了残差。

PTAV

H. Fan and H. Ling, “Parallel tracking and verifying: A framework for real-time and high accuracy visual tracking,” 2017

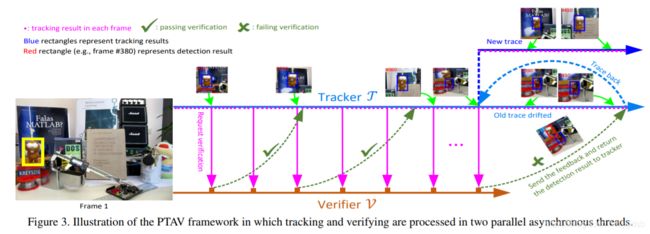
整个跟踪算法分为两部分：跟踪器T和验证器V。跟踪器T负责预测目标位置，发送验证信号，并保证算法实时性；验证器V负责验证跟踪器T的预测位置结果是否可靠，并在必要时修正跟踪器T的预测结果。

STCT

L. Wang, W. Ouyang, X. Wang, and H. Lu, “Stct: Sequentially training convolutional networks for visual tracking,” in CVPR. IEEE, 2016

MUSTer

Z. Hong, Z. Chen, C. Wang, X. Mei, D. Prokhorov, and D. Tao, “Multistore tracker(muster): A cognitive psychology inspired approach to object tracking,” in CVPR. IEEE, 2015, pp. 749–758

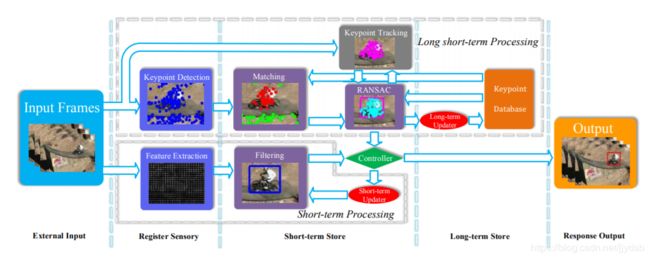
Short-term Processing：传统的DCF
Long short-term Processing：RANSAC加上关键点匹配
因为网上看到只公开了.p文件，所以没兴趣看

SRDCF与deepSRDCF

M. Danelljan, G. Hager, F. S. Khan, and M. Felsberg, “Learning spatially regularized correlation filters for tracking,” in ICCV. IEEE, 2015
M. Danelljan, G. Hager, F. S. Khan, and M. Felsberg, “Convolutional features for correlation filter based tracking,” in ICCVW. IEEE, 2015.
思想很简单，既然随着位移量的增加，循环位移产生的负样本的真实性会降低，那么给循环位移产生的样本集加个权重，位移量越少，样本越真实，则权重越大，惩罚项越小；位移量越大，样本越不真实，则权重越小，惩罚项越大。
公式下一次再说吧

SRDCFdecon

M. Danelljan, G. Hager, F. S. Khan, and M. Felsberg, “Adaptive decontamination of the training set: A unified formulation for discriminative visual tracking,” in CVPR. IEEE, 2016, pp. 1430–1438.

联合学习跟踪模型和样本权重，降低损坏样本的权重，增大正确样本的权重。

STRCF

F. Li, C. Tian, W. Zuo, L. Zhang, and M. Yang, “Learning Spatial-Temporal Regularized Correlation Filters for Visual Tracking,” in CVPR. IEEE, 2018

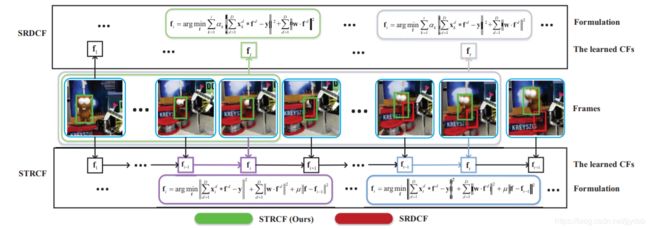
DMSRDCF

S. Gladh, M. Danelljan, F. S. Khan, and M. Felsberg, “Deep motion features for visual tracking,” in ICPR. IEEE, 2016, pp. 1243–1248
appearance information + motion features
运动信息由光流法估计

CCOT 与 ECO

M. Danelljan, A. Robinson, F. S. Khan, and M. Felsberg, “Beyond correlation filters: Learning continuous convolution operators for visual tracking,” in ECCV. Springer, 2016
M. Danelljan, G. Bhat, F. S. Khan, and M. Felsberg, “Eco: Efficient convolution operators for tracking,” in CVPR. IEEE, 2017, pp. 6931–6939

CSRDCF

A. Lukei, T. Voj, L. .n Zajc, J. Matas, and M. Kristan, “Discriminative Correlation Filter with Channel and Spatial Reliability,” in CVPR. IEEE, 2017

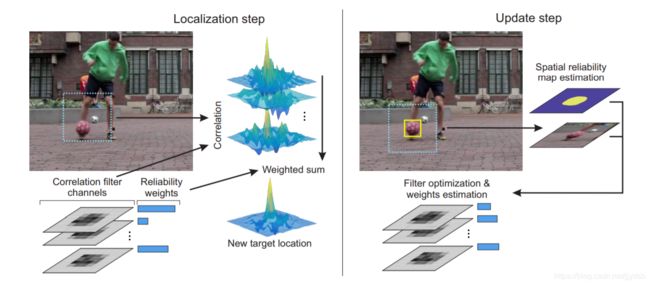
空间上只关注目标，不关注背景，就是分割产生mask，可以获得非矩形框，利用贝叶斯估计mask
channel上每个通道上乘以权重
【未看完，待续】
update 2019.01.11
Todo