常见的排序算法 (冒泡、选择、插入、希尔、归并、快速排序、堆排序、桶排序) 以及优化

1、冒泡排序

冒泡排序是一种简单的排序算法。它重复地走访要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作就是重复地进行直到不需要再进行交换为止，也就是说该数列已经排序完成。这个算法的名字由来就是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

算法描述

1. 比较相邻的元素，如果第一个比第二个大，就交换它们两个；
2. 对每一对相邻的元素作同样的工作，从开始第一队到尾部的最后一对，这样在最后的元素应该会是最大的数；
3. 针对所有的元素重复以上的步骤，直到排序完成

复杂度分析

• 最佳情况：$O(n)$
• 最差情况：$O(n^2)$
• 平均时间复杂度：$O(n^2)$
• 空间复杂度为 : $O(1)$
• 稳定的排序算法
  冒泡排序只会比较相邻的两个元素，如果两个元素相等，我想你是不会再无聊地把他们俩交换一下的

代码实现

void Bubble_Sort(int *arr, int n) {
	if(arr == NULL) return;
	for(int i = 0; i < n - 1; ++i){
		for(int j = 0; j < n - i - 1; ++j){
			if(arr[j] > arr[j+1]){
				int temp = arr[j];
				arr[j] = arr[j+1];
				arr[j+1] = temp;    
			}
		}
	}
} 

1.冒泡排序的第一个优化 — 有序序列不再遍历

对于整体有序的情况如 $1,2,3,4,5,6,7,9,8,10$ ，显然可能只需要少数的几次交换就可以达到排序后的结果。
所以在某一次遍历的时候，如果发现没有进行任何交换，那么说明现在的序列已经有序了，所以这时我们就可以结束这次排序。

void Bubble_Sort(int *arr, int n) {
	if(arr == NULL) return;
	for(int i = 0; i < n - 1; ++i){
		int flag = 0; // 用来标记是否进行过交换 
		for(int j = 0; j < n - i - 1; ++j){
			if(arr[j] > arr[j+1]){
				int temp = arr[j];
				arr[j] = arr[j+1];
				arr[j+1] = temp;    
				flag = 1;
			}
		}
		if (flag == 0) return; // 若这轮排序没有进行交换，则结束排序 
	}
} 

2.冒泡排序的第二个优化 — 修改遍历长度

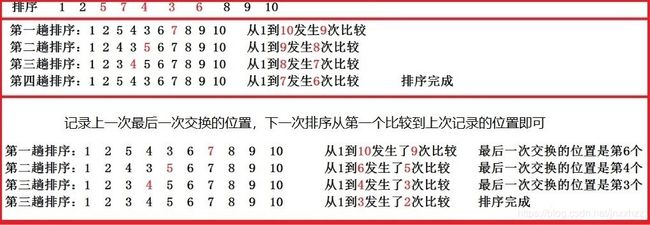
对于某次交换后，最后一段都已变成有序的情况，显然我们可以跳过后面已经有序的那一段数字的比较。
比$n-i-1$更快的方式就是记录最后一次进行交换的位置，下一次的遍历只到这里即可

void Bubble_Sort(int *arr, int n) {
	if(arr == NULL) return;
	int k = n - 1; // 用来记录最后一次交换的位置 
	for(int i = 0; i < n - 1; ++i){
		int flag = 0; // 用来标记是否进行过交换 
		for(int j = 0; j < k ; ++j){
			if(arr[j] > arr[j+1]){
				int temp = arr[j];
				arr[j] = arr[j+1];
				arr[j+1] = temp;    
				flag = j; // 记录最后一次进行交换的位置 
			}
		}
		if (flag == 0) return; // 若这轮排序没有进行交换，则结束排序 
		k = flag; //否则下一轮的排序只需要遍历到最后一个进行交换的位置即可 
	}
}

3.冒泡排序的第三个优化 — 鸡尾酒排序

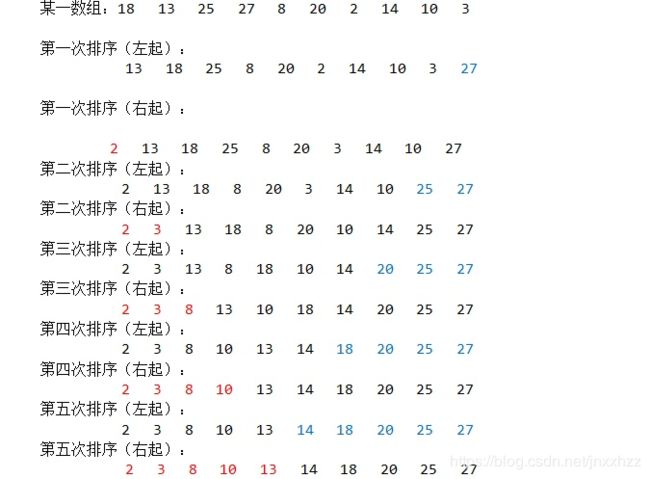
鸡尾酒排序（Cocktail Sort）（又名：双向冒泡排序 (Bidirectional Bubble Sort)、波浪排序 (Ripple Sort)、摇曳排序 (Shuffle Sort)、飞梭排序 (Shuttle Sort) 和欢乐时光排序 (Happy Hour Sort)）

与冒泡排序不同的是，此算法双向进行排序，鸡尾酒排序等于是冒泡排序的轻微变形

鸡尾酒排序与冒泡排序的区别在于：鸡尾酒排序每次进行从低到高 然后 从高到低两次排序，而冒泡排序每次都是从低到高去比较序列里的每个元素。
鸡尾酒排序可以得到比冒泡排序稍微好一点的效能，原因是冒泡排序只能从一个方向进行比对，每次循环只移动一个元素

void Cocktail_Sort(int *arr,int n){
    int left = 0;
    int right = n - 1;
    while(left < right){
        //前半轮，将最大元素放到后面
        for(int i = left ; i < right ; ++i)
            if(arr[i] > arr[i+1])
                swap(arr[i],arr[i+1]);
                
        right--;
        //后半轮，将最小元素放到前面
        for(int i = right ; i > left ; --i)
            if(arr[i] < arr[i-1])
                swap(arr[i],arr[i-1]);
        left++;
        
    }
}

2、选择排序

选择排序是一种简单直观的排序算法。它的工作原理：首先在末排序列中找到最小（大）的元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）的元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

算法描述

1. 初始状态：无序区为 $R[1...n]$ ，有序区 $L$ 为空；
2. 第 $i$ 趟排序 $(i=1,2,3...n-1)$ 开始时，当前有序区和无序区分别为 $L[1...i-1]$ 和 $R[i...n]$ 。该趟排序从当前无序区中选出关键字最小的记录 $R[k]$ ，将它与无序区的第 $1$ 个记录 $R[i]$ 交换，使无序区记录个数增加 $1$ 个变为$L[1...i]$ ，无序区记录个数减少 $1$ 个变为 $R[i+1...n]$ ;
3. $n-1$趟排序结束，数组有序化。

复杂度分析

• 最佳情况：$O(n^2)$
• 最差情况：$O(n^2)$
• 平均时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$
• 不稳定的排序算法
  例如序列 $[5，5^{\ast }，3]$第一趟就将第一个 $[5]$ 与 $[3]$ 交换，导致第一个 $[5]$ 挪动到第二个 $[5^{\ast }]$ 后面，那么两个 $[5]$ 就不再保持原本的相对位置了

算法实现

void SelectionSort(int *arr, int n){
	if(arr == NULL) return;
	for(int i = 0; i < n; ++i){
		int minIndex = i;
		for(int j = i; j < n; ++j)
			if(arr[j] < arr[minIndex])
				minIndex = j;
		int temp = arr[minIndex];
		arr[minIndex] = arr[i];
		arr[i] = temp;
	}
}

3、插入排序

插入排序算法是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用 $in-place$ 排序（即只需用到 $O(1)$ 的额外空间的排序），因而在从后向前扫描的过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

算法描述

1. 从第一个元素开始，该元素可以认为已经被排序；
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描；
3. 如果该元素（已排序）大于新元素，将该元素移到下一个位置；
4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
5. 将新元素插入到该位置后；
6. 重复步骤 2~5

算法分析

• 最佳情况：$O(n)$
• 最坏情况：$O(n^2)$
• 平均时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$
• 稳定的排序算法
  因为对于未排序的数据是从前往后按顺序插入已排序序列，并且已排序序列中是从后往前找到第一个小于等于新元素的位置，那么如果存在相等的元素，新元素应该插入在已排序序列中相同元素之后，那么相同元素的相对位置并没有发生改变

代码实现

void InsertionSort(int *arr, int n){
	if(arr == NULL) return;
	for(int i = 0; i < n - 1; i++){
		int currnet = arr[i+1];
		int preIndex = i;
		while(preIndex >= 0 && currnet < arr[preIndex]){
			arr[preIndex + 1] = arr[preIndex];
			preIndex--;
		}
		arr[preIndex + 1] = currnet;
	}
}

4、希尔排序

希尔排序是希尔于 $1959$年 提出的一种排序算法。希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破 $O(n^2)$ 的第一批算法之一。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

希尔排序是把记录按一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组所包含的关键词越来越多，当增量减至 $1$ 时，整个文件恰被分成一组，算法便终止。

算法描述

在此我们选择希尔排序增量为 $gap=length/2$，缩小增量继续以 $gap=gap/2$ 的方式，这种增量选择我们可以用一个序列来表示，$n/2,(n/2)/2,...,1$ ,称为增量序列。
希尔排序的增量序列的选择与证明是个数学难题，我们选择的这个增量序列是比较常用的，也是希尔建议的增量，称为希尔增量，但其实这个增量序列不是最优的。

1. 选择一个增量序列 $t1,t2,...,tk$ ,其中 $ti>tj,tk=1$ ;
2. 按增量序列个数 $k$ ，对序列进行 $k$ 趟排序；
3. 每趟排序，根据对应的增量 $ti$ ，将待排序序列分隔成若干长度为 $m$ 的子序列，分别对各子序列进行直接插入排序。
4. 仅增量因子为1时，整个序列作为一个表来处理，子序列长度即为整个序列的长度。仅增量因子为1时，整个序列作为一个表来处理，子序列长度即为整个序列的长度。

算法分析

• 最佳情况：$O(nlogn)$
• 最坏情况：$O(nlogn)$
• 平均时间复杂度：$O(nlogn)$
• 空间复杂度：$O(1)$
• 不稳定的排序算法
  例如序列 $[1,10,5,5^{\ast }]$ ,排序结果是 $[1,5^{\ast },5,10]$，显然 $[5]$ 和 $[5^{\ast }]$ 的相对位置发生了改变

代码实现

void Shell_Sort(int *arr, int n){
	if(arr == NULL) return;
	int temp, gap = n / 2;
	while(gap > 0){
		for(int i = gap; i < n; i++){
			temp = arr[i];
			int preIndex = i - gap;
			while(preIndex >= 0 && arr[preIndex] > temp){
				arr[preIndex + gap] = arr[preIndex];
				preIndex -= gap;
			}
			arr[preIndex + gap] = temp;
		}
		gap /= 2;
	}
}

5、归并排序

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，始终都是 $O(nlogn)$ 的时间复杂度。代价是需要额外的内存空间

归并排序是建立在归并操作上的一种有效的排序算法。该算法是分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使得每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

算法描述

1. 把长度为n的输入序列分为两个长度为n/2的子序列；
2. 对这两个子序列分别采用归并排序；
3. 将两个排序好的子序列合并成一个最终的排序序列。

复杂度分析

• 最佳情况：$O(n)$
• 最坏情况：$O(nlogn)$
• 平均时间复杂度：$O(nlogn)$
• 空间复杂度：$O(n)$
• 稳定的排序算法

代码实现

void Merge(int arr[], int p, int q, int r){
    int n1 = q - p + 1;
    int n2 = r - q;
    int *L;
    L = (int*)malloc(sizeof(int) * n1);
    int *R;
    R = (int*)malloc(sizeof(int) * n2);
    int i = 0;
    for(; i < n1; ++i) L[i] = arr[i + p];
    int j = 0;
    for(; j < n2; ++j) R[j] = arr[j + q + 1];
    
    i = j = 0;
    int k = p;
    while(i != n1 && j != n2){
        if(L[i] <= R[j])
            arr[k++] = L[i++];
        else
            arr[k++] = R[j++];
    }
	while(i < n1) arr[k++] = L[i++];
    while(j < n2) arr[k++] = R[j++];
	free(L);free(R);
}

void MergeSort(int arr[], int p, int q){
    if(p < q){
        int r = (p + q) / 2;
        MergeSort(arr, p, r);
        MergeSort(arr, r + 1, q);
        Merge(arr,p, r, q);
    }
}

6、快速排序

快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。
在C++的STL中，sort采用的就是快速排序，并且大致加入了下面三种优化。
快速排序是在原序列越有序时越慢，越无序则越快

算法描述

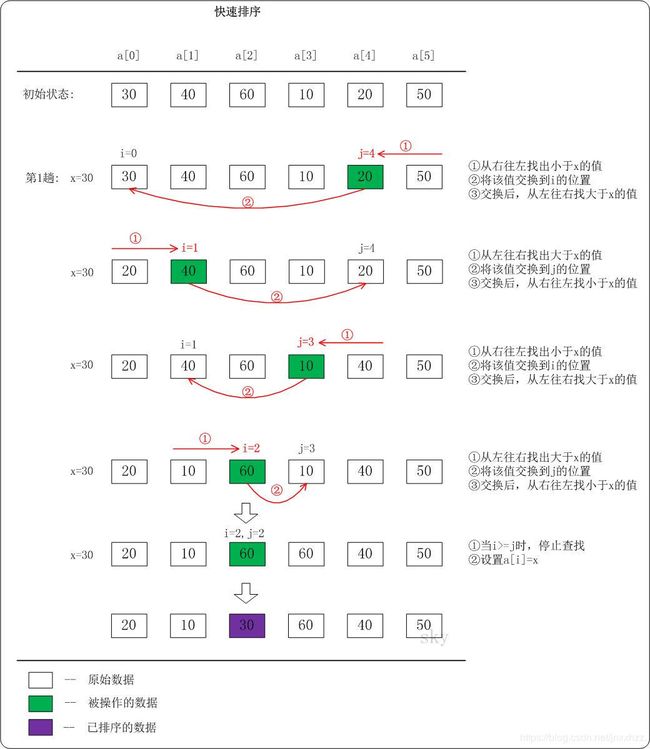
1. 每次从当前数列中跳出一个元素，称为“基准”
2. 重新排序当前数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区操作；
3. 递归将把 小于基准值元素的子数列 和 大于基准值元素的子数列 分别进行排序。
   

复杂度分析

• 最佳情况：$O(nlogn)$
• 最坏情况：$O(n^2)$ （数据有序时会达到最慢的速度）
• 平均时间复杂度：$O(nlogn)$
• 空间复杂度：$O(nlogn)$
• 不稳定的排序算法

代码实现

int partition(int *a, int left, int right){
    int key = a[left];
    while(left < right){
        while(left < right && a[right] >= key) right--;     
        a[left] = a[right];
        while(left < right && a[left] <= key) left++;       
        a[right] = a[left];   
    }
    a[left] = key;                                          
    return left;    
}
void Qsort(int *a, int left, int right){
    if(left < right){                                       
        int pos = partition(a, left, right);
        Qsort(a, left, pos - 1);                           
        Qsort(a, pos + 1, right);
    }
}

1.快速排序的第一种优化 — 随机化快排 / 三数取中 / 取中间值等

随机化快排 / 三数取中 / 取中间值 等优化，都是基于选择的"基准"不同来达到提速的效果。
因为快速排序在排序一个已经有序的序列时，我们会发现每次分区的时候两个区的长度分别为 $1$ 和 $n-1$ ,这样的话就会导致$O(n^2)$ 的复杂度，但是实际上如果我们对于一个有序的序列，每次选中间值的话，就可以均分这两段区间。
所以这类优化的思路都是基于选择的"基准"不同来使划分区间的时候尽可能平均。

int partition(int *a, int left, int right){
	//int tmp = rand() % (right - left + 1) + left; 
	int tmp = (right + left) >> 1; 
	swap(a[left],a[tmp]);
    int key = a[left];
    while(left < right){
        while(left < right && a[right] >= key) right--;     
        a[left] = a[right];
        while(left < right && a[left] <= key) left++;       
        a[right] = a[left];   
    }
    a[left] = key;                                          
    return left;    
}
void Qsort(int *a, int left, int right){
    if(left < right){                                       
        int pos = partition(a, left, right);
        Qsort(a, left, pos - 1);                           
        Qsort(a, pos + 1, right);
    }
}

2.快速排序的第二种优化 — 三路排序

显然在大数据量的排序下，会出现很多重复的数据，这时候，所有跟"基准"相等的元素并没有必要再进入之后的分区，所以这时我们可以将区间分成三段，而不是之前的两段。

排序的时候依旧递归左右两个区间，但是中间与基准相等的这一段区间显然没有必要再继续进行递归。

void QSort3Ways(int *arr, int l, int r) {
	if (r <= l) return;
    int temp = arr[l];
    int lt = l;        // arr[l+1...lt] <  pivot
    int gt = r + 1;    // arr[gt...r]   >  pivot
    int i = l + 1;     // arr[lt+1...i) == pivot
    while (i < gt) {
        if (arr[i] < temp) {
            swap(arr[i], arr[lt + 1]);
            i++;
            lt++;
        } else if (arr[i] > temp) {
            swap(arr[i], arr[gt - 1]);
            gt--;
        } else {
            i++;
        }
    }
    swap(arr[l], arr[lt]);
    QSort3Ways(arr, l, lt - 1);
    QSort3Ways(arr, gt, r);
}

3.快速排序的第三种优化 — 使用插入排序

在子序列比较小的时候，其实插入排序是比较快的，因为对于有序的序列，插排可以达到 $O(n)$ 的复杂度，如果序列比较小，则和大序列比起来会更容易有序，这时候使用插入排序效率要比快速排序高。
实现方法也很简单：快排是在子序列元素个数变成 $1$ 时，才停止递归，我们可以设置一个阈值,当长度小于一个固定的数值时使用插入排序，否则继续递归使用快速排序 (在很多论文中会使用 $7$ 作为这个阈值，在大量数据测试下，$7$ 对整体代码的速度提升是最多的)

4.综合三种优化以后的快速排序

void QSort3Ways(int *arr, int l, int r) {
	if (r - l <= 7) {
        InsertSort(arr, l, r);
        return;
    }
    swap(arr[l],arr[rand()%(r-l+1) + l]);
    int temp = arr[l];
    int lt = l;        // arr[l+1...lt] <  pivot
    int gt = r + 1;    // arr[gt...r]   >  pivot
    int i = l + 1;     // arr[lt+1...i) == pivot
    while (i < gt) {
        if (arr[i] < temp) {
            swap(arr[i], arr[lt + 1]);
            i++;
            lt++;
        } else if (arr[i] > temp) {
            swap(arr[i], arr[gt - 1]);
            gt--;
        } else {
            i++;
        }
    }
    swap(arr[l], arr[lt]);
    QSort3Ways(arr, l, lt - 1);
    QSort3Ways(arr, gt, r);
}

7、堆排序

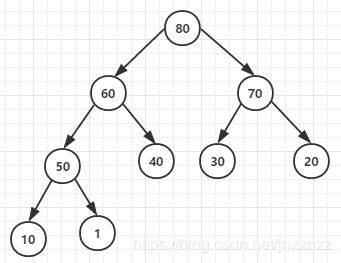
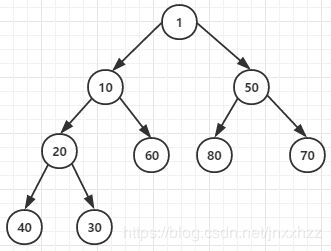
堆排序是指利用堆这种数据结构所涉及的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足下面的性质：子结点的键值或索引总是小于（或者大于）它的父结点。
堆排序是一种树形选择排序，在排序过程中可以把元素看成是一颗完全二叉树，每个节点都大（小）于它的两个子节点，当每个节点都大于等于它的两个子节点时，就称为大顶堆，也叫堆有序； 当每个节点都小于等于它的两个子节点时，就称为小顶堆。

大顶堆

小顶堆

算法描述

1. 将初始待排序关键字序列 $(R1,R2,...,Rn)$ 构建成大（小）根堆，此堆为初始的无序区；
2. 将堆顶元素 $R[1]$ 与最后一个元素 $R[n]$ 交换，此时得到新的无序区 $(R1,R2,...,Rn)$ 和新的有序区 $(Rn)$ ，且满足$R[1,2...,n-1]<=R[n]$;
3. 由于交换后新的堆顶 $R[1]$ 可能违反堆的性质，因此需要对当前无序区 $(R1,R2,...,Rn-1)$调整为新堆
4. 然后再次将 $R[1]$ 与无序区最后一个元素交换，得到新的无序区 $(R1,R2,...,Rn-2)$ 和新的有序区 $(Rn-1,Rn)$。
5. 不断重复此过程直到有序区的元素个数为 $n-1$ ,则整个排序过程完成。

复杂度分析

• 最佳情况：$O(nlogn)$
• 最坏情况：$O(nlogn)$
• 平均时间复杂度：$O(nlogn)$
• 空间复杂度：$O(1)$
• 不稳定的排序算法

代码实现

void downAdjust(int *arr,int low, int high) {   
//low表示最低的元素下标,high表示数组的最后一个元素的下标
	int current = low, lchild = current * 2;   
	//lchild表示左孩子
	while (lchild < high) {//如果左孩子存在
		//如果右孩子存在,且右孩子的值大于当前结点值
		if (lchild + 1 < high && arr[lchild] < arr[lchild + 1]) {
			lchild = lchild + 1;   //改成右节点
		}
 
		if (arr[lchild] > arr[current]) {
			swap(arr[lchild], arr[current]);
			current = lchild;
			lchild = current * 2;
		}
		else {
			break;
		}
	}
}
 
void HeapSort(int *arr,int n) {
	for (int i = n / 2; i >= 0 ; --i) 
		downAdjust(arr,i, n);
	
	for (int i = n - 1; i > 0; --i) {
		swap(arr[0], arr[i]);
		downAdjust(arr,0, i);
	}
}

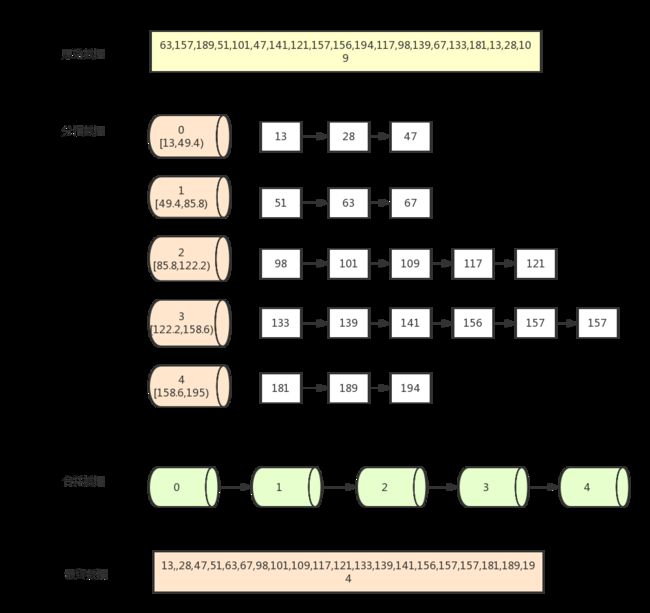
8、不基于比较的桶排序

算法描述

1. 设置固定空桶数
2. 将数据放到对应的空桶中
3. 将每个不为空的桶进行排序
4. 拼接不为空的桶中的数据，得到结果
   

复杂度分析

• 最佳情况：$O(n+k)$
• 最坏情况：$O(n+k)$
• 平均时间复杂度：$O(n+k)$
• 空间复杂度：$O(n)$
• 稳定排序算法

代码实现

void Bucket_sort(int *arr,int n){
	int a[10000];
	for(int i = 0 ; i < n ; ++i)  //循环读入5个数
	{
		scanf("%d",&t);  //把每一个数读到变量t中
		a[t]++;  		 //进行计数
	}
	for(int i = 0 ; i <= 10 ; ++i)  //依次判断a[0]~a[10]
		for(int j = 1 ; j <= a[i] ; ++j)  //出现了几次就打印几次
        	printf("%d ",i);
}

9、神仙算法 — 睡眠排序

多线程睡眠排序…开个玩笑，这是个有趣的算法

void sleepSortHelper(int i) {
    this_thread::sleep_for(chrono::microseconds(i*10000));
    std::cout << i << " ";
}
void sleepSort(int *arr,int size) {

    for (int i = 0; i < size; i++)
    {
        std::thread t(sleepSortHelper,arr[i]);
        t.detach();
    }

}
void main() {
    sleepSort(arr, 7);
    getchar();
}

总结

各种排序的稳定性，时间复杂度和空间复杂度总结：
我们比较时间复杂度函数的情况：对 $n$ 较大的排序记录。一般的选择都是时间复杂度为 $O(nlogn)$ 的排序方法。

时间复杂度

1. $O(n^2)$ 排序
   　　各类简单排序 ; 直接插入 ; 直接选择 ; 冒泡排序；
2. $O(nlogn)$ 排序
   　　快速排序 ; 堆排序 ; 归并排序 ；
3. $O(n^{1.3-2})$排序　　希尔排序
4. $O(n)$ 排序
   　　 桶排序，基数排序等

稳定性

排序算法的稳定性:若待排序的序列中，存在多个具有相同关键字的记录，经过排序，这些记录的相对顺序保持不变，则称该算法是稳定的；若经排序后，记录的相对顺序发生了改变，则称该算法是不稳定的。

稳定性的好处：排序算法如果是稳定的，那么从一个键上排序，然后再从另一个键上排序，第一个键排序的结果可以为第二个键排序所用。另外，如果排序算法稳定，可以避免多余的比较；

1. 稳定
   　　 冒泡排序，插入排序，归并排序，桶排序
2. 不稳定
   　　 选择排序，希尔排序， 快速排序，堆排序

原序列是否有序对排序算法的影响

• 当原序列有序或基本有序时，插入排序和冒泡排序将大大减少比较次数和移动记录的次数，时间复杂度可降至 $O(n)$；
• 当原序列基本有序时，将蜕化为冒泡排序，时间复杂度提高为$O(n^2)$
• 原序列是否有序，对选择排序、堆排序、归并排序和桶排序的时间复杂度影响不大。