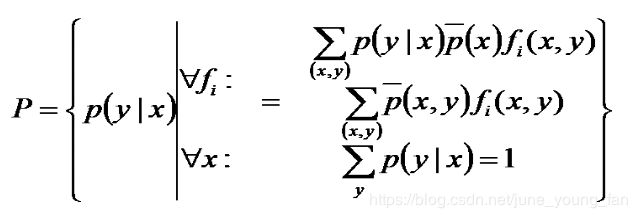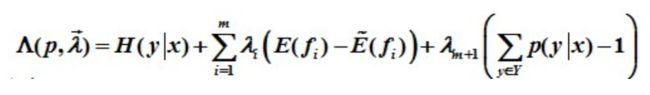关于最大熵的解释
什么是熵
熵是随机变量不确定性的度量,不确定性越大,熵值越大;若随机变量退化成定值,熵为0。
如果没有外界干扰,随机变量总是趋向于无序,在经过足够时间的稳定演化,它应该能够达到的最大程度的熵。
最大熵
为了准确的估计随机变量的状态,我们一般习惯性最大化熵,其原则是承认已知事物(知识),且对未知事物不做任何假设,没有任何偏见。
无偏原则
下面举个大多数有关最大熵模型的文章中都喜欢举的一个例子。
一篇文章中出现了“学习”这个词,那这个词是主语、谓语、还是宾语呢?
换言之,已知“学习”可能是动词,也可能是名词,故“学习”可以被标为主语、谓语、宾语、定语等等。
令x1表示“学习”被标为名词, x2表示“学习”被标为动词。
令y1表示“学习”被标为主语, y2表示被标为谓语, y3表示宾语, y4表示定语。
这些概率值加起来的和必为1,即:
P(x1) + P(x2) = 1 and P(y1) + P(y2) + P(y3) + P(y4) = 1
则根据无偏原则,认为这个分布中取各个值的概率是相等的,故得到:
P(x1) = P(x2) = 0.5 and P(y1) = P(y2) = P(y3) = P(y4) = 0.25
因为没有任何的先验知识,所以这种判断是合理的。如果有了一定的先验知识呢?
举个例子:若已知:“学习”被标为定语的可能性很小,只有0.05,即,剩下的依然根据无偏原则,可得:
P(x1) = P(x2) = 0.5 and P(y1) = P(y2) = P(y3) = 0.95 / 3
再进一步,当“学习”被标作名词x1的时候,它被标作谓语y2的概率为0.95,即:
P(y2 | x1) = 0.95
此时仍然需要坚持无偏见原则,使得概率分布尽量平均。但怎么样才能得到尽量无偏见的分布?
实践经验和理论计算都告诉我们,在完全无约束状态下,均匀分布等价于熵最大(有约束的情况下,不一定是概率相等的均匀分布。 比如,给定均值和方差,熵最大的分布就变成了正态分布 )。
于是,问题便转化为了:计算X和Y的分布,使得H(Y|X)达到最大值,并且满足下述条件:
P(x1) + P(x2) = 1 and P(y1) + P(y2) + P(y3) + P(y4) = 1
P(y4) = 0.05 and P(y2 | x1) = 0.95
因此,也就引出了最大熵模型的本质,它要解决的问题就是已知X,计算Y的概率,且尽可能让Y的概率最大(实践中,X可能是某单词的上下文信息,Y是该单词翻译成me,I,us、we的各自概率),从而根据已有信息,尽可能最准确的推测未知信息,这就是最大熵模型所要解决的问题。
转换成公式,便是要最大化下述式子H(Y|X):
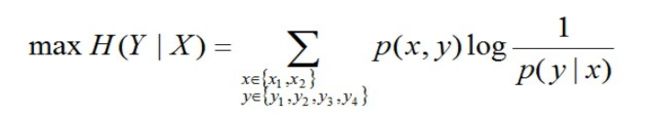
已知X,计算Y的最大可能的概率,且满足以下4个约束条件:
P(x1) + P(x2) = 1 and P(y1) + P(y2) + P(y3) + P(y4) = 1
P(y4) = 0.05 and P(y2 | x1) = 0.95
最大熵模型的表示
至此,我们可以写出最大熵模型的一般表达式了,如下:
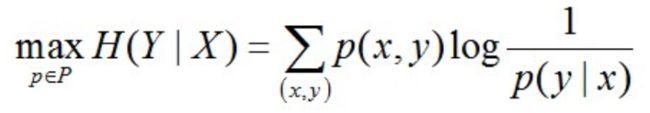
其中:P是X上满足条件的概率分布。
再继续推导之前,我们先对特征、样本、特征函数定义一下:
- 特征:(x,y) ;
- x:这个特征中的上下文信息;
- y:这个特征中需要确定的信息;
- 样本:关于某个特征(x,y)的样本,特征所描述的语法现象在标准集合里的分布为:(xi,yi),其中,yi是y的一个实例,xi是yi的上下文。
对于一个特征(x0,y0),定义特征函数:

特征函数关于经验分布 p ‾ ( x , y ) \overline{p}(x, y) p(x,y)在样本中的期望值是:
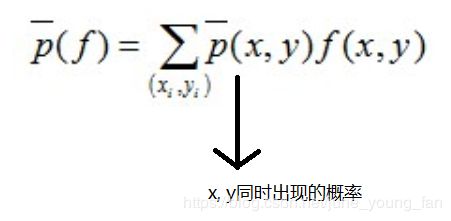
特征函数关于模型P(Y|X)与经验分布 p ‾ ( x ) \overline{p}(x) p(x)的期望值为:

换言之,如果能够获取训练数据中的信息,那么上述这两个期望值相等。
现回到最大熵模型的表达式上来。注意到p(x,y) = p(x) * p(y|x),但因为p(x)不好求,所以一般用样本中x出现的概率" p ‾ ( x ) \overline{p}(x) p(x)"代替x在总体中的分布概率“p(x)”,从而得到最大熵模型的完整表述如下:
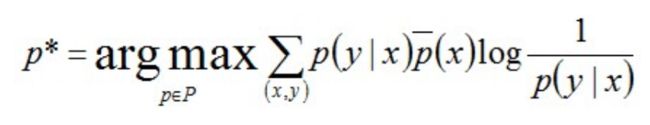
该问题是已知若干条件,要求若干变量的值使得目标函数(熵)最大,其数学本质是最优化问题(Optimization Problem),其约束条件是线性的等式,而目标函数是非线性的,所以该问题属于非线性规划(线性约束)(non-linear programming with linear constraints)问题,故可通过引入Lagrange函数将原约束最优化问题转换为无约束的最优化的对偶问题。
凸优化中的对偶问题
考虑到机器学习里,不少问题都在围绕着一个“最优化”打转,而最优化中凸优化最为常见,所以为了过渡自然,这里简单阐述下凸优化中的对偶问题。
一般优化问题可以表示为下述式子:

其中,subject to导出的是约束条件,f(x)表示不等式约束,h(x)表示等式约束。
然后可通过引入拉格朗日乘子λ和v,建立拉格朗日函数,如下:
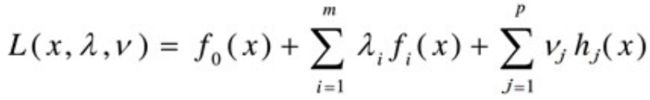
对固定的x,Lagrange函数L(x,λ,v)为关于λ和v的仿射函数。
对偶问题的极大化
针对原问题,首先引入拉格朗日乘子λ0,λ1,λ2, …, λi,定义拉格朗日函数,转换为对偶问题求其极大化:
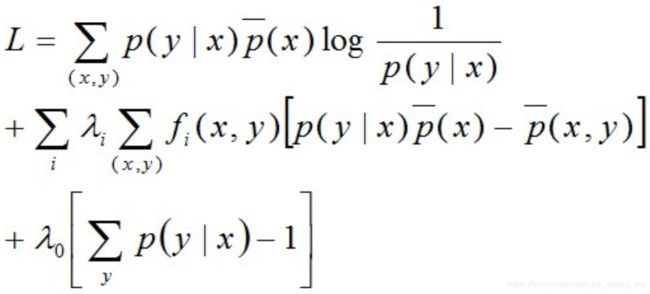
然后求偏导可得:
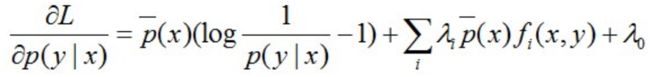
注:上面这里是对P(y|x)求偏导,即只把P(y|x)当做未知数,其他都是常数。因此,求偏导时,只有跟P(y0|x0)相等的那个"(x0,y0)"才会被微分,其他的(x,y)都不是关于P(y0|x0)的系数,是常数项。
令上述的偏导结果等于0,解得:
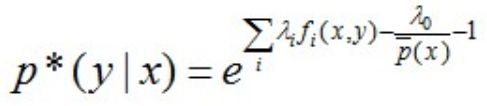
进一步转换:
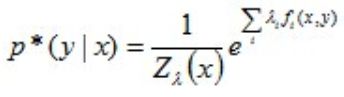
其中,Z(x)称为规范化因子。
因为:
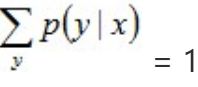
所以有:
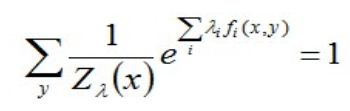
即:
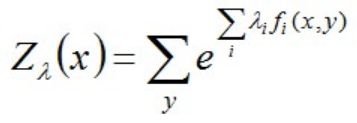
现将求得的最优解P*(y|x)带回之前建立的拉格朗日函数L:
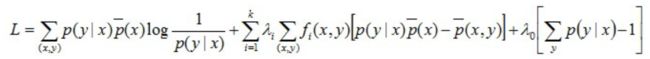
得到关于λ的式子:
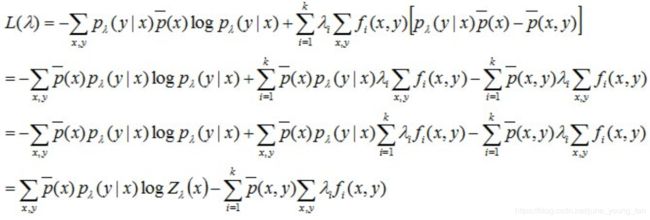
再回过头来看这个式子:
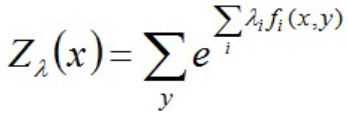
可知,最大熵模型属于对数线性模型,因为其包含指数函数,所以几乎不可能有解析解。换言之,即便有了解析解,仍然需要数值解。那么,能不能找到另一种逼近?构造函数f(λ),求其最大/最小值?
相当于问题转换成了寻找与样本的分布最接近的概率分布模型,如何寻找呢?你可能想到了极大似然估计。
最大熵模型的极大似然估计
极大似然估计MLE的一般形式表示为:
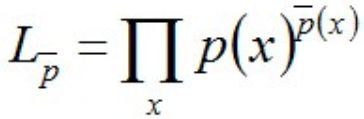
其中,p(x)是对模型进行估计的概率分布, p ‾ ( x ) \overline{p}(x) p(x)是实验结果得到的概率分布。
进一步转换,可得:
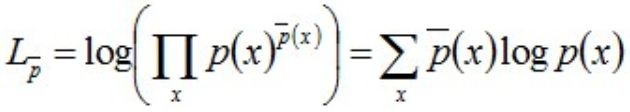
对上式两边取对数可得:
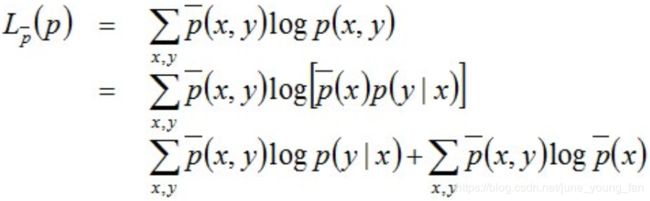
因上述式子最后结果的第二项是常数项(因为第二项是关于样本的联合概率和样本自变量的式子,都是定值),所以最终结果为:
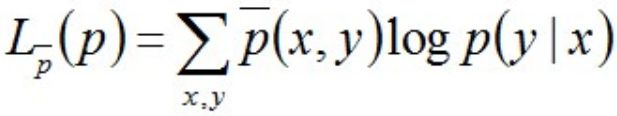
至此,我们发现极大似然估计和条件熵的定义式具有极大的相似性,故可以大胆猜测它们极有可能殊途同归,使得它们建立的目标函数也是相同的。 我们来推导下,验证下这个猜测。
将之前得到的最大熵的解带入MLE,计算得到:
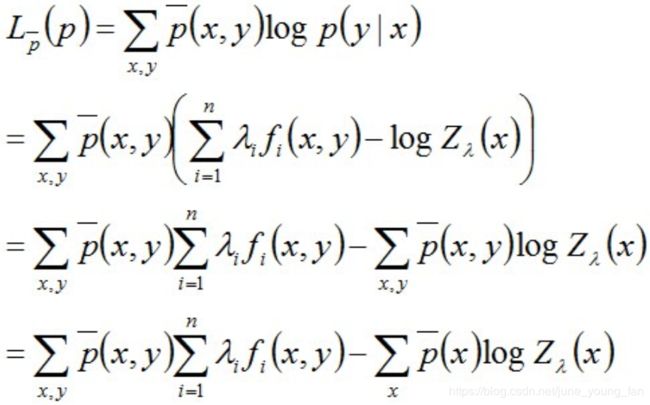
注:上述式子的最后一步推导中,根据P(x,y) = P(x) * P(y|x),和之前得到的结论 ∑ y p ( y ∣ x ) \sum_y{p(y|x)} ∑yp(y∣x) = 1 推出。
然后拿这个通过极大似然估计得到的结果跟之前得到的对偶问题的极大化解对比下,发现二者的右端果然具有完全相同的目标函数。换言之,之前最大熵模型的对偶问题的极大化等价于最大熵模型的极大似然估计。
且根据MLE的正确性,可以断定:最大熵的解(无偏的对待不确定性)同时是最符合样本数据分布的解,进一步证明了最大熵模型的合理性。两相对比,熵是表示不确定性的度量,似然表示的是与知识的吻合程度,进一步,最大熵模型是对不确定度的无偏分配,最大似然估计则是对知识的无偏理解。
本文转自:http://www.360doc.com/content/14/1111/22/20290918_424405228.shtml