STM32F1做RSA,AES数据加解密,MD5信息摘要处理
转自: https://blog.csdn.net/qq_31878855/article/details/69396791
一.加密算法分类及选取
按照密钥的特点加密算法分为两大类一类是对称密钥算法,一类是非对称加密算法。
1.1对称算法介绍
对称加密算法其实就是加密方和解密方所用的密钥是相同的,意思就是你们通讯的双方都必须知道这个密钥,如果密钥发生改变就必须一起改变。坏处就是密钥不好管理,你必须把你的密钥告诉别人,别人才能解密,好处就是运算速度快。
1.2对称算法分类
①DES(Data Encryption Standard):数据加密标准,速度较快,适用于加密大量数据的场合。
②3DES(Triple DES):是基于DES,对一块数据用三个不同的密钥进行三次加密,强度更高。
③AES(Advanced Encryption Standard):高级加密标准,是下一代的加密算法标准,速度快,安全级别高;
1.3非对称算法介绍
非对称密钥就是加密和解密所用到的密钥不一样,意思就是你可以将你的一个密钥直接公开发给另外一个人,另外一个人用你发给他的那个密钥来进行数据加密,将密文发给你,你用你的另外一个密钥解开(用一个密钥加的密,只能用另一个密钥解开),公开的那个叫公钥,保密的那个叫私钥。好处就是密钥你不需要两个人大好商量,你可以随意变动,增大安全性,坏处就是运算速度慢。
1.4非对称算法分类
①RSA:由 RSA 公司发明,是一个支持变长密钥的公共密钥算法,需要加密的文件块的长度也是可变的。
②ECC(Elliptic Curves Cryptography):椭圆曲线密码编码学。
③DSA(Digital Signature Algorithm):数字签名算法,是一种标准的 DSS(数字签名标准)。
1.5算法的选取
①对称算法的选取:AES算法在对称加密算法中具有速度快,安全性能高,消耗资源少的特点。该有的优点都有了,所以在对称算法选取中AES是比较明智的选择。
②非对称算法的选取:ECC和RSA在相同的安全性能上,运行速度和消耗资源方面都要比RSA好,但是算法原理相对复杂(其实咱也不研究)自己实现比较困难,所以在非对称选取上选用ECC比较合适。(问:为什么这里用RSA?答:RSA都做完了,你跟我说这个。)
1.6散列加密算法介绍
散列为对信息的提取,结果为一个固定长度的数值,不能根据数值结果推导出原文。散列算法最主要的性质为只要源文件的一位发生改变,那么产生的数值将发生明显的变化,且对于不同的文件内容所产生的数值一定不同。主要用处就是去验证你的那一份信息有没有被别人改变,到底是不是你的。
1.7散列算法分类
①MD5(Message Digest Algorithm 5):是RSA数据安全公司开发的一种单向散列算法,非可逆,相同的明文产生相同的密文。
②SHA(Secure Hash Algorithm):可以对任意长度的数据运算生成一个160位的数值;
1.8散列算法选取
MD5和SHA-1都是从MD4 推导出来的,所以性能上非常的相似,最大的不同在于SHA-1产生的是160bit,MD5为128bit,所以安全性能上SHA-1要高一点,但是速度慢一些,介于是在单片机上运行所以选取MD5做散列算法。
现在呢算法是选好了,但是怎么去实现呢?还是从原理下手比较好。
二.算法原理分析
算法原理我们简单了解一下就行了,笔者只对用到算法原理做一个简单的介绍,因为这些算法代码都不需要我们自己写,网上有大量的算法代码,我们了解只是为了能看的懂别人的代码或者在用开源库的时候知道参数怎么填写就够了,这就叫做站在巨人的肩膀上。
对于加解密算法的话给一个统一的解释,加解密算法就是将你的密钥和你的明文经过一定的算法混合后得到密文,对密文和密钥进行逆运算可以重新恢复明文的一个过程。在这过程当中就算别人知道你是怎么算出来的,但是他不知道你的密钥是推到不出明文的。后面的加解密算法都是遵循这个原理的。(我这个人呢喜欢用一句简单的话去解释一些比较复杂的东西,最大的原因是我比较喜欢物理,在物理学中,总是能有一个比较简单的定理去解释一些比较复杂的一些东西,而且用它做题的话你会发现非常轻松,数学也如此但是太抽象)
2.1.RSA加解密原理
参考:http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html
RSA是1987由三位在麻省理工大学工作的数学家首次提出来的,目前用的非常广泛。每个非对称算法的出现总是会基于数学上的难题,RSA的数学难题是:对于两个非常大的质数,对他们的乘积我们非常容易得到,但是对于这个乘积因式分解却非常的困难。基于这个数学难题就衍生出了非常著名的RSA非对称算法(这个难题的原理是不是简单,因为因式分解我们小学都学过)。那到底RSA算法怎么实现的呢?。
2.1.1密钥的选取
要使用RSA算法的话首先我们得选取两个非常大的质数p和q,有。
n = p*q;
n的长度呢就是我们所说的RSA密钥的长度,RSA密钥的长度决定RSA算法的安全性,这东西越长我们的数据就会越安全,也不是越长越好,因为你的计算机速度跟不上去啊。就目前全世界公开了的能够破解的最大密钥长度为700多位(二进制哦),所以呢我们的密钥选取1024位是相对安全的,2048位是绝对安全的(重要场合)。
有了n之后我们需要得到n的欧拉函数,欧拉函数其实就是用来计算在小于等于n的数值中有多少个数与n互质。
互质的意思就是两个正整数之间除了1之外没有其他的公共因子,列如:一个数可以拆分出不同数的乘积,这些不同的数就是这个数的因子,公因子就是两个正整数的因子当中相同的因子,如果这两个数的公因子只有1的话,那么我们就说这两个数互质。
有定理->如果一个数是质数的话,那么比他小的每一个数都和他互质。则有
p的欧拉函数φ(p) =p-1;
q的欧拉函数φ(q) =q-1;
那么φ(n)=φ(p*q)=φ(p)*φ(q)(证明略)
就可以得到
φ(n) = (p-1)*(q-1);
接下来我们就要随机选取正整数e,要求 1< e<φ(n),并且e和φ(n)互质。我们选取的这个e和n一般公开,组成公钥(n,e),其中n称为模数,e称为公钥指数,对于加密指数的选取大部分人都选为65537(0x010001),以及我们后面的代码加密指数都选取65537,因为他本来就是公开的,所以选多大要求不高。
公钥选好了接下来要选取私钥了d了,对于d应该满足
e*d = 1(modφ(n))
意思就是e*d除以φ(n)余数为1,该式等价于
e*d - 1 = k*φ(n)
怎么求出d,这需要用到“扩展欧几里得算法”,其中d的解肯定不止一个,怎么算咱们就不管了。
我们选取的d呢是保密的,(n,d)组成私钥,d称为私钥指数,私钥d呢我们选取越大越好,这样他越不容易被破解,一般和模数n位数相同,如果密钥长度n为1024位,那么私钥指数d一般也为1024位。
我们刚刚选取了(p,q,n,e,d)五个数,其中p和q没用可以销毁,但是不能公开,(n,e)组成公钥,(n,d)组成私钥。
我们现在来看看别人知道n和e到底能不能求出私钥d来。
根据 e*d = 1(modφ(n))可知,别人想求出d就得知道φ(n),而φ(n) = (p-1)*(q-1),所以想求出d就得求出p和q。
然而 p*q = n,所以想要破解我们的RSA密钥就必须对n做因式分解,众所周知这是一个数学上的难题,且n越大这道题就越难。
2.1.2利用密钥加解密
利用RSA加密时需注意,你的密文长度不能大于你的秘钥长度减去11个字节,比如我们的密钥长度是1024位128字节,则明文长度不能大于128-11=117个字节,不管你明文数据长度是多少,输出的密文长度都等于你的密钥长度128个字节,RSA的加解密公式非常的简洁。
①加密(公钥)
对于我们的明文x(x必须是整数且小于模数n)加密有:
x^e % n = y
其中 y 为输出的密文,%为对n取余,余数为y。
②解密(私钥)
对于密文y解密有:
y^d % n = x
2.1.3RSA加解密示例
由上可以知道RSA的运算一直都是大数运算,还有可怕的y^d,幸好前人都已经有了完整的算法可以快速的计算。
我参考的例子为百度文库的一个例子。连接如下:
找不到连接了我放到百度云上去。
这个代码是我个人人为比较好的例子,其中包含生成密钥,加密,解密,所有的函数都是自己实现的,缺点就是资源占用多,速度慢,非常不适合在单片机上运行。
2.2AES加解密原理
AES的原理我们不必深究,AES加密主要分为四个基本步骤:字节替代,行位移,列混淆,轮密钥加,AES的明文是放在4*4矩阵中的,一个矩阵经过上面四步为一轮,加解密的刚开始都需要进行轮密钥加步骤,之后按顺序执行上面四个步骤,在最后一轮中不执行列混淆操作,因为最后一轮加列混淆并不会加大AES算法的安全性,只会降低算法效率。在每一轮中都会参一点密钥,每一轮的密钥都是由初始密钥扩展得到。密钥长度可选128位(10轮),192位(12轮),256位(14轮),由此可知循环轮数越多,秘钥长度越长,信息加密也就会越安全。一般我们的AES密钥选取128位就已经足够了。
2.2.1AES算法密钥的选取
在网上的示例代码中我们都会看到有一个叫S盒子的中西,这个东西主要是在进行字节替代的时候用到的,这个S盒子存放了00~FF共256中字节替代的结果,逆S盒子是解密用的。
我们本次选取的AES密钥长度为128位共16个字节,格式如下:
uint8_t Aes128_Key[16] =
{
0x40, 0x41, 0x42, 0x43,
0x44, 0x45, 0x46, 0x47,
0x4c, 0x4d, 0x4e, 0x4f
};
2.2.2AES加解密
AES为了适应不同的安全性要求和传输需求有多种加密模式,主要有ECB、CBC、CFB和OFB加密模式。
ECB(电子密码本模式:Electronic codebook)是最简单的块密码加密模式,加密前根据加密块大小(如AES为128位)分成若干块,之后将每块使用相同的密钥单独加密,解密同理。
CBC模式(密码分组链接:Cipher-block chaining)CBC模式对于每个待加密的密码块在加密前会先与前一个密码块的密文异或然后再用加密器加密。第一个明文块与一个叫初始化向量的数据块异或。CBC模式相比ECB有更高的保密性,但由于对每个数据块的加密依赖与前一个数据块的加密所以加密无法并行。与ECB一样在加密前需要对数据进行填充,不是很适合对流数据进行加密。
CFB模式(密文反馈:Cipher feedback)与ECB和CBC模式只能够加密块数据不同,CFB能够将块密文(Block Cipher)转换为流密文(Stream Cipher)。
OFB与CFB一样都非常适合对流数据的加密,OFB由于加密和解密都依赖与前一段数据,所以加密和解密都不能并行。
本次利用ECB模式对明文进行加密,采用128位的AES密钥,所以加密的明文必须为16个字节的整数倍,且输出的密文长度等于进行加密的明文长度(明文填充之后的长度)。
2.2.3AES加解密示例
这个示例是我在网上找的,一个老外写的,比较好的放到百度云上。
- 1
- 2
2.3MD5信息摘要原理
对MD5算法简要的叙述可以为:MD5以512位分组来处理输入的信息,且每一分组又被划分为16个32位子分组,经过了一系列的处理后,算法的输出由四个32位分组组成,将这四个32位分组级联后将生成一个128位散列值。
2.3.1MD5用处
MD5没有所谓的密钥,只是把你的明文生成一个固定长度的散列值。
①可以防止你的文件被别人更改,可以在你的文件没给别人之前或者自己写的东西不希望别人更改,你可以对你之前的文件做MD5运算,得到一个MD5值保存起来,当你发现别人好像动了你的或者传输过程怀疑数据丢失了,把之后的文件也做一个MD5值,把两个MD5值做对比,就知道你的文件到底是不是和以前一模一样。
②可以把你的密码做MD5值保存起来,密码验证的时候不直接比较密码,比较MD5值,这样别人看不到你的密码原文。
③数字签名,我们本次的实际用处也是做数字签名使用。
2.3.2MD5示例
放到百度云上。
- 1
- 2
2.4数字签名
数字签名的作用是确定别人的身份用的。
“数字签名”一般的做法是:A先计算出文件 M 的 MD5值,再对MD5值进行RSA加密(这个步骤就是签名),再把M(文件 M 不要加密,第三方可以查阅)和加密后的MD5值传送给B,B 再用 A 的公钥来解密刚才得到的加密 MD5值,如果能解密,那就说明这个文件是A 发的,具有法律效应。再计算出得到的文件 M 的 MD5值,再和刚才解密出来的 MD5值比较(这个步骤叫验证签名),如果一致就说明文件 M 在传输过程中没有被修改。
三.加解密算法在STM32F1上的实现
3.1具体要求
客户要求在进行wifi数据传输时对所传输的数据进行加密处理,以及服务器和客户端之间的身份认证。具体实现为客服端登录前首先交换RSA公钥(里面含有ca数字签名),交换公钥后客户端将得到服务器的RSA公钥和一个CA数字签名,CA数字签名为服务器端将服务器公钥做MD5数字摘要后利用CA中心认证私钥做RSA加密后形成的,客服端需要将得到的服务器RSA公钥做MD5数字摘要,之后用CA公钥去解密CA数字签名,将解密后得到的MD5值和服务器公钥形成的MD5值做对比,成功则认证通过,服务器端也一样。身份认证通过后服务器端随机生成128bit的AES密钥,利用客户端公钥加密后发送给客户端,客户端解密,之后的数据传输都使用AES加密方式。是不是有点绕?刚开始我也分不清楚,但是后来按照这个步骤做了之后渐渐就懂了,下面就来看看具体我怎么实现的。
3.2加密算法库的选取
找这个东西真的是费尽啊,刚开始我将我在PC上运行成功过的RSA加解密例子直接搬到STM32上面,发现一堆的问题(个人技术不行),最最主要的就是堆栈溢出问题了,你要知道博主用的是STM32F103芯片,RAM才20k而且芯片要做的事情还不止wifi的数据加解密,还有很多的其他事情。最主要的原因就是上面的那个RSA例子里面的解密函数里面开了一个长度为65535的一个数组,你知道多大吗,对差不多64K,吓人不。后来发现后把自己都下了一跳,怪不得我怎么调整内存都没用。(结论:遇到问题应该沉着冷静不应该烦躁抱怨)现在呢跑是跑成功了,但是还是有一个致命的问题,解密速度跟不上去,客户要求解密时间不能太长,最长为1s左右的时间,我使用上面的代码,一个十进制为11位的密钥,解密时间花费了差不多4.5s的样子,十进制13位的花了将近8s。我不敢想象1024bit会是一个什么样子,而且用1024bit的密钥单片机的内存也不够用了。我都和客户说了这没办法的实现不了,人家当面就教训我,“事情还没做之前不要轻易的下结论,曾经就有人用1024bit的密钥解密就花了一秒钟”(其实我是不信的)。但口头上还是答应了试试看。
然后我就在网上使劲的找,首先找到了polarssl开源库,百度百科上这样介绍“PolarSSL源码,也许是最小巧的ssl代码库。高效、便于移植和集成。尤其适合嵌入式应用。”,看上面的关键字,最小巧的ssl,尤其适合嵌入式运用,哇,当时就觉得苦日子终于到头了,然后我就搜polarssl怎么移植到stm32上,后面发现polarssl被ARM收购了改名为mbedTLS,那敢情好呀,还是自家人,瞬间觉得它就是我一直要找的那个东西。立马进入ARM官网下载这个mbedtls库,下载完后我是懵逼的,我发现我不会移植,怎么移怎么错后面索性把c文件都放进去,还是错。哎,当时就在感慨人生喜怒无常啊。
就在这内忧外患的时候出现了一个人,对、就是那个1024bit只花了1s的那个人,我不知道他是害我的还是来救我的。然后我从他手上竟然得到了ST官方的一个密码库(stm32cryptographic),匪夷所思,网上竟然没透出半点风声,这下好了上次来的是堂兄弟这次直接来的是亲兄弟。好了又到了下载移植的时候了,这个亲兄弟移植起来比较简单,最主要的就是h文件的放入了,c文件不用担心人家已经做好了lib文件,直接放进去就行了,人家也有官方的测试代码,缺什么放什么就行了。还有一个地方要注意,有些h文件会关联很多的h文件,事实上在一个h文件中我们能用到的就那么一点东西,不需要整个h文件都包含进来,直接把我们所需要的内容复制到h文件里面也是可以的。
3.2.1stm32-cryp-lib的使用
在st下载的官方库中有大量的算法列子供我们参考,路径:en.x-cube-cryptolib\STM32CubeExpansion_Crypto_V3.1.0\Fw_Crypto\STM32F1\Projects\STM32F103RB-Nucleo,这个路径下都是keil工程文件是可以直接下载带stm32f1上运行的工程。
①RSA加密函数
int32_t RSA_Encrypt(RSApubKey_stt *P_pPubKey,
const uint8_t *P_pInputMessage,
int32_t P_InputSize,
uint8_t *P_pOutput);
成功返回0,
RSApubKey_stt *P_pPubKey 为公钥结构体指针原型为
typedef struct
{
uint8_t pmModulus; /!< RSA Modulus 为我们的模数n 装在一个大的数组里面*/
int32_t mModulusSize; /!< Size of RSA Modulus 模数n的字节大小 1024 位为128/
uint8_t pmExponent; /!< RSA Public Exponent 公钥指数,一般为 65537*/
int32_t mExponentSize; /!< Size of RSA Public Exponent 公钥指数字节大小 /
}RSApubKey_stt;
const uint8_t *P_pInputMessage :为我们需要加密的明文信息指针。
int32_t P_InputSize:为我们输入的信息字节大小。
uint8_t *P_pOutput:输出的密文数据大小 注意是个指针。
②RSA解密函数
int32_t RSA_Decrypt(RSAprivKey_stt * P_pPrivKey,
const uint8_t * P_pInputMessage,
uint8_t *P_pOutput,
int32_t *P_OutputSize);
typedef struct
{
uint8_t pmModulus; /!< RSA Modulus 模数n和公钥相同*/
int32_t mModulusSize; /!< Size of RSA Modulus 模数大小/
uint8_t pmExponent; /!< RSA Private Exponent 私钥指数*/
int32_t mExponentSize; /!< Size of RSA Private Exponent 私钥指数大小/
}
RSAprivKey_stt;
const uint8_t * P_pInputMessage 要解密的密文。
uint8_t *P_pOutput 解密输出的明文。
int32_t *P_OutputSize 输出明文的大小
③ RSA签名认证函数
int32_t STM32_RSA_Verify_Md5(RSApubKey_stt *P_pPubKey,
uint8_t *Md5_Digest ,
const uint8_t *P_pSignature)
RSApubKey_stt *P_pPubKey 公钥结构体。
uint8_t *Md5_Digest MD5值16个字节
const uint8_t *P_pSignature 数字签名
本函数会对P_pSignature利用P_pPubKey进行解密,最后和Md5_Digest进行一对一比较,比较成功返回SIGNATURE_VALID(一个宏定义意思是验证成功)
④MD5数字摘要函数
int32_t STM32_MD5_HASH_DigestCompute(uint8_t* InputMessage, uint32_t InputMessageLength,
uint8_t MessageDigest, int32_t MessageDigestLength)
uint8_t* InputMessage 要进行MD5运算的输入信息。
uint32_t InputMessageLength 输入信息的长度。
uint8_t *MessageDigest 输出的MD5值。
int32_t* MessageDigestLength 输出的MD5长度。
⑤AES加密函数
AES加解密函数ECB模式的
int32_t STM32_AES_ECB_Encrypt(uint8_t* InputMessage,
uint32_t InputMessageLength,
uint8_t *AES256_Key,
uint8_t *OutputMessage,
uint32_t *OutputMessageLength)
uint8_t* InputMessage 输入信息
uint32_t InputMessageLength 输入信息长度
uint8_t *AES256_Key AES密钥别看叫什么256,可以输入128的,只要在函数体中将 AESctx.mKeySize = 16; 变量赋值16就可以了
uint8_t *OutputMessage 输出的密文信息
uint32_t *OutputMessageLength 输出密文长度
⑥AES解密函数
int32_t STM32_AES_ECB_Decrypt(uint8_t* InputMessage,
uint32_t InputMessageLength,
uint8_t *AES256_Key,
uint8_t *OutputMessage,
uint32_t *OutputMessageLength)
函数的几个形参和加密是一样的。
st密码库下载地址http://www.st.com/content/st_com/en/products/embedded-software/mcus-embedded-software/stm32-embedded-software/stm32-standard-peripheral-libraries-expansions/stm32-cryp-lib.html
四.项目实现以及和服务器的对接
把所有的准备工作都做完了以后,可以将加密算法移植到我们具体的项目中去了,在STM32中在出厂前已经将RSA的公钥私钥,CA数字签名和CA公钥烧写在STM32的flash上了。
4.1 身份认证
在wifi连接上服务器上后,客户端首先发起交换密钥请求,客户端将自己的RSA公钥,CA数字签名发送给服务器,服务器将自己的公钥,CA数字签名(是利用CA的私钥对服务器公钥机密的一段密文),以及加密后(利用的是客户端的公钥加的密)的AES密钥(为了减小STM32的负担,随机密钥由服务器产生就随身份认证的信息一起发送过来了)发送给客户端。客户端接收到服务器的信息后,首先对服务器公钥做MD5处理,然后调用STM32密码库中的签名认证函数进行认证,通过则进行后续操作,失败客户端进入休眠状态(wifi不可操作),服务器进行类似的处理。
4.2 解密AES密钥
将得到的包含AES密钥的密文利用RSA私钥进行解密,将得到AES的随机密钥。随后的数据传输将利用这个密钥和AES算法进行加密传输。
项目上的代码不好贴上面还有好多的细节问题需要处理,大多数是C语言的数据处理问题,有什么问题可以留言我。服务器利用的是openssl加密库,可以实现生成rsa,加密,解密等等一系列操作,比STN32的加密库要强好多好多。
4.3 利用openssl生成RSA密钥对
利用 openssl genrsa -out rsa_private_key.pem 1024 生成rsa密钥,这个文件包含了私钥和公钥。
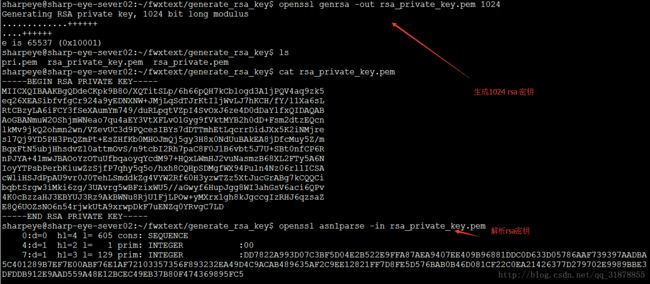
利用 openssl asn1parse -in rsa_private_key.pem
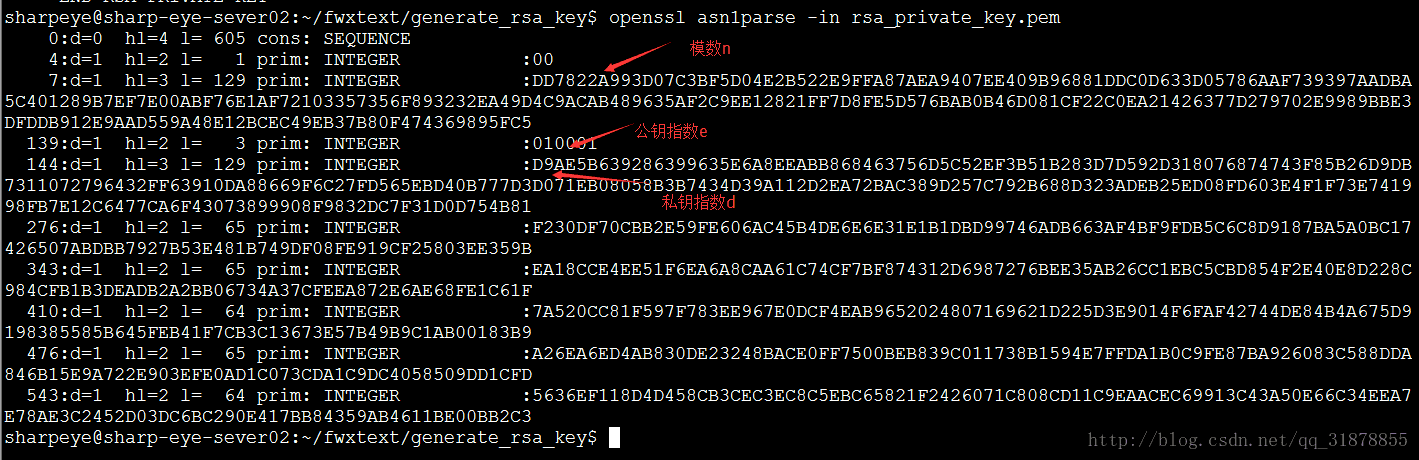
说起这个密钥问题到现在都有点心酸负责服务器那边的人死活不认n,e,d,服务器那边出来的密钥都是什么PKCS#8格式的说是需要我这边来进行处理,我当时也是懵逼的这又是些什么东西啊。无奈之下又去研究PKCS#8和n,e,d的关系,有衍生出一系列的RSA密钥的规范问题,但是这不是最恐怖的。最恐怖的是STM32F103C8T6的flash爆炸了。我也有心无力,最后我只能从服务器端入手找到了如上的方法,经过几经周转对方终于答应放弃了他们原先的密码库换成了openssl,之后也还有许多的问题这里就说说这个相对拖得比较久一点的问题。
在线加解密网站。
http://web.chacuo.net/netrsakeypair
我把我在网上翻阅的资料放到百度云上。链接:http://pan.baidu.com/s/1jIvazfK 密码:5jis