Kaggle案例之泰坦尼克船员幸存预测（sklearn机器学习库）

无意间在网易云课堂上找了一个Kaggle案例，泰坦尼克获救船员预测，在此之前我是从没接触过kaggle，毕竟是刚入门的小白，看着视频，算是真正实战了一次，主要是在这个过程中学到了很多东西。
下面视频地址
http://study.163.com/course/courseLearn.htm?courseId=1003551009#/learn/video?lessonId=1004052093&courseId=1003551009

还有数据集，是在GitHub里面找的
https://github.com/fayduan/Kaggle_Titanic
里面有大佬的ipython 源码，不过我也没仔细去看。还是按照视频上的一步一步下来。
首先是整体的流程我大概总结了一下。

1. 拿到数据集分析数据
2. 找出数据集中每个特征中是否含有缺失值或者异常值，填充缺失值
3. 将特征中为字符的特征值转换为数值型，比如将性别男女用0和1表示
4. 分析数据集适合采用什么算法进行预测，比如适合用分类算法还是适合用回归算法
5. 建立特征工程（这算是整个过程下来最重要的）
6. K阶交叉验证，划分数据集（k-1份训练，1份验证，每次换一个。重复k次，用来调优），

7. 将交叉验证后的数据集扔进算法中进行训练及测试准确率。

   接下来代码实现（按照视频教程实现）。
   1导入数据，进行分析

import pandas as pd
import numpy as np
titanic = pd.read_csv("数据集/titannike/train.csv")
#将数据集中所有的样本特征属性打印出来，每一列的相关数据信息
titanic

2数据预处理

#数据预处理， 填充缺失值以及将特征中含有字符的转换为数值型

#将年龄这一列的数据缺失值进行填充
titanic["Age"] = titanic["Age"].fillna(titanic["Age"].median())
#titanic
print(titanic.describe())
#打印这一列特征中的特征值都有哪些
print(titanic["Sex"].unique())
#将性别中的男女设置为0 1 值 把机器学习不能处理的自字符值转换成能处理的数值
#loc定位到哪一行，将titanic['Sex'] == 'male'的样本Sex值改为0
titanic.loc[titanic["Sex"] == "male","Sex"] = 0
titanic.loc[titanic["Sex"] == "female","Sex"] = 1
#print(titanic["Sex"].unique)
#print(titanic["Embarked"].unique())
#通过统计三个登船地点人数最多的填充缺失值
titanic["Embarked"] = titanic["Embarked"].fillna("S")
#将登船地点同样转换成数值
titanic.loc[titanic["Embarked"] == "S","Embarked"] = 0
titanic.loc[titanic["Embarked"] == "C","Embarked"] = 1
titanic.loc[titanic["Embarked"] == "Q","Embarked"] = 2
print(titanic["Embarked"].unique())

3通过线性回归进行预测（拿回归做分类确实有点鸡肋）

import numpy as np


#将sklearn中的线性回归的类导入进去，采用二分类进行分类预测
from sklearn.linear_model import LinearRegression
#交叉验证库，将训练集进行切分交叉验证取平均
from sklearn.cross_validation import KFold

#这里，人为的先选取部分有用特征
predictors = ["Pclass","Sex","Age","SibSp","Parch","Fare","Embarked"]
#将线性回归方法导进来
alg = LinearRegression()
#将m个样本分成三份 n_folds 代表的是交叉验证划分几层（几份）
kf = KFold(titanic.shape[0],n_folds=3,random_state=1)#该行代码做的是交叉验证

predictions = []
for train,test in kf:
    #将训练数据拿出来，对原始数据取到建立好的特征 然后取出用于训练的那一部分
    train_predictors = (titanic[predictors].iloc[train,:])
    #print(train_predictors)

    #获取到数据集中交叉分类好的标签，即是否活了下来
    train_target = titanic["Survived"].iloc[train]
    #print(train_target)

    #将数据放进去做训练
    alg.fit(train_predictors,train_target)
    #训练完后，使用测试集进行测试误差
    test_predictions = alg.predict(titanic[predictors].iloc[test,:])
    predictions.append(test_predictions)

#使用线性回归得到的结果是在区间[0,1]上的某个值，需要将该值转换成0或1
predictions = np.concatenate(predictions,axis=0)
#print(predictions)
#print(type(titanic["Survived"]))

predictions[predictions >.5] = 1
predictions[predictions <=.5] = 0
predictions.dtype = "float64"


titanic["Survived"] = titanic["Survived"].astype(float)

print("测试数据总数量",len(predictions))
#print("正确的数量：",sum(predictions[predictions == titanic["Survived"]]))
print("正确的数量：",sum(predictions == titanic["Survived"]))
accuracy = sum(predictions == titanic["Survived"]) / len(predictions)

print("准确率为：",accuracy)

结果：

这里有个坑：我按照视频教程一步一部来，结果最后测试准确率竟然只有26%左右，想着是不是predictors里面的数据类型跟实际数据集里面Survived标签不一样，然后我都将类型转换为了float64，结果，没有什么变化，只是从26%提高到了36%,显然主要不是这的原因，最后无意间发现是python2跟python3的语法问题。

#这是Python2的代码
sum(predictions[predictions == titanic["Survived"]])
#在Python3中应该为
sum(predictions == titanic["Survived"])

然后准确率就达到78%左右了，
显然这个结果并不算好，所以要试一下用其他算法，比如逻辑回归，或者随机森林。（在此还没想到建立特征工程了）

进行下面的步骤之前，我们首先要了解一些参数的意义

random_state
        作为每次产生随机数的种子
        作为随机种子对于调参过程是很重要的，如果每次都用不同的随机种子。即使参数值没变，每次出来的结果也会不同，不利于比较不同模型的结果
        任一个随机样本都有可能导致过度你和，可以用不同的随机样本建模来减少过拟合到的可能
n_estimators
        定义了需要用到的决策树的数量


min_samples_split
        定义了书中一个节点所需要用来分裂的最少样本数
        可以避免过拟合，如果用于分类的样本数太小，模型可能只试用于用来训练样本的分类，而用较多的样本数则可以避免这个问题
        如果设定的值过大，就可能出现欠拟合现象，所以可以用cv值(离散数量)考量调节效果
min_samples_leaf
        定义了树中终点节点所需要用来分裂的最少样本数
        同样，可以防止过度拟合
        不均等分类问题中，一般这个参数需要设定为较小的值。因为大部分少数类别含有的样本都比较小
min_weight_fraction_leaf
        和上面的min_simples_leaf 很像，，不同的是这个参数需要被设定为较小的值，因为大部分少数类别含有的样本都比较小
        #2和#3只需要定义一个就行了
max_depth
        定义和树的最大深度
        也可以控制过拟合，树越深，越容易过拟合
        也可以用CV值检验
max_leaf_nodes
        定义了决策树里最多能有多少个终点节点
        这个属性可能在上面的max_depth里就被定义了，深度为n的二叉树就有最多2的n次方的终点节点
        如果定义max_leaf_nodes GBM就会忽略前面的  max_depth
max_features
        决定了用于分类的特征树，是认为随机定义的
        根据经验一般选择总特征数的平方根就可以工作的很好，最多可以尝试总特征数的30%-40%

4通过逻辑回归进行预测判断

#通过逻辑回归做分类
from sklearn import cross_validation
from sklearn.linear_model import LogisticRegression
alg = LogisticRegression(random_state = 1)
#使用逻辑回归做交叉验证
score = cross_validation.cross_val_score(alg,titanic[predictors],titanic["Survived"],cv=3)
print(score.mean())
#out  0.787878787879

比用线性回归得分稍微高一点，但是也没搞多少
5用随机森林模型

#随机森林模型
from sklearn import cross_validation
from sklearn.ensemble import RandomForestClassifier
predictors = ["Pclass","Sex","Age","SibSp","Parch","Fare","Embarked"]

#各个参数的意思 n_estimators 表示的是指定随机森林中需要多少的决策树  min_samples_split min_samples_leaf 
#   表示的是划分树的控制的结束条件，划分到哪个节点上停止划分。 一个通过样本个数，一个通过叶子节点个数 
alg = RandomForestClassifier(random_state=1,n_estimators = 100,min_samples_split=4,min_samples_leaf=2)

#依然做三次交叉验证
kf = cross_validation.KFold(titanic.shape[0],n_folds=3,random_state=1)
scores = cross_validation.cross_val_score(alg,titanic[predictors],titanic["Survived"],cv=kf)

print(scores.mean())

#out  0.814814814815

可以看出，明显比线性回归和逻辑回归得到的分数高很多
当然，分数应该还能再高点，因为我们到目前为止还没建立特征工程，特征工程部做好，其实用什么算法，用什么交叉验证都是无用的

6:通过再一次分析数据集，我们可以衍生出来两个特征
1 通过每个乘客的SibSp 和Parch 亲友人数建立一个家庭大小特征FamilySize
2用点神学，是不是获救的可能性跟每个乘客的名字或者名字长度有关系
然后这就衍生出来两个特征
代码实现

#建立特征工程 根据数据集中已有特征进行特征分析，可以添加相关特征
#将船上所有人的亲属朋友关系加起来，新建一个特征，用来表示每个人的亲属关系
#提取的第一个特征
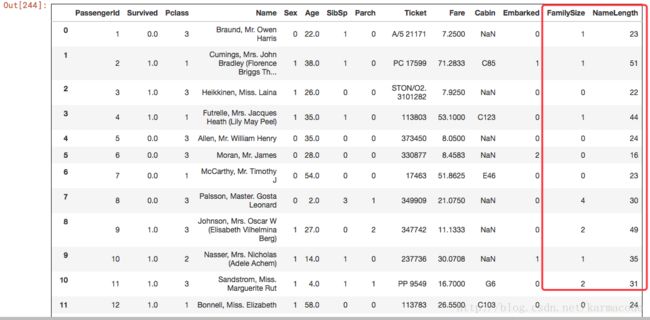
titanic["FamilySize"] = titanic["SibSp"] + titanic["Parch"]
#提取的第二个特征 根据名字长度
titanic["NameLength"] = titanic["Name"].apply(lambda x:len(x))
titanic

接下来提特征

import re
import pandas as pd
def get_title(name):
    title_search = re.search(' ([A-Za-z]+)\.',name)

    if title_search:
        return title_search.group(1)
    return ""

titles = titanic["Name"].apply(get_title)
print(pd.value_counts(titles))
#将称号转换成数值表示
title_mapping = {"Mr":1,"Miss":2,"Mrs":3,"Master":4,"Dr":5,"Rev":6,"Major":7,"Col":7,"Mlle":8,
                 "Mme":8,"Don":9,"Lady":10,"Countess":10,"Jonkheer":10,"Sir":9,"Capt":7,"Ms":2
                }

for k,v in title_mapping.items():
    titles[title == k] = v

print(pd.value_counts(titles))
#添加Title特征
titanic["Title"] = titles

7:通过特征选择库，对选择的特征进行进一步筛选，看看哪些特征比较重要

import numpy as np

#通过 feature_selection 对选择的特征进行进一步选择，画出保护直方图可以直观的看出哪些特征对最终的准确率影响较大
from sklearn.feature_selection import SelectKBest,f_classif
import matplotlib.pyplot as plt

predictors = ["Pclass","Sex","Age","SibSp","Parch","Fare","Embarked","FamilySize","Title","NameLength"]

selector = SelectKBest(f_classif,k=5)
selector.fit(titanic[predictors],titanic["Survived"])

scores = -np.log10(selector.pvalues_)

plt.bar(range(len(predictors)),scores)

plt.xticks(range(len(predictors)),predictors,rotation="vertical")
plt.show()

predictors = ["Pclass","Sex","Fare","Title"]
alg = RandomForestClassifier(random_state=1,n_estimators=50,min_samples_split=8,min_samples_leaf=4)


#依然做三次交叉验证
kf = cross_validation.KFold(titanic.shape[0],n_folds=3,random_state=1)
scores = cross_validation.cross_val_score(alg,titanic[predictors],titanic["Survived"],cv=kf)

print(scores.mean())

同时，我在这里面又加上了随机森林模型，对建立好的特征进行再一次预测
发现准确率达到了81.9%,比没有建立特征工程的随机森林模型多了大约0.5%
，果然还是有用的。

最后，将两个算法结合着使用，Boosting和逻辑回归结合使用

from sklearn.ensemble import GradientBoostingClassifier
import numpy as np

algorithms = [
    [GradientBoostingClassifier(random_state=1,n_estimators=50,max_depth=6),
     ['Pclass','Sex','Age','SibSp','Parch','Fare','Embarked','FamilySize','NameLength','Title']],
    [LogisticRegression(random_state=1),
     ['Pclass','Sex','Age','SibSp','Parch','Fare','Embarked','FamilySize','NameLength','Title']] 

]

kf = KFold(titanic.shape[0],n_folds=3,random_state=1)  
predictions = []  
for train, test in kf:  
    train_target = titanic['Survived'].iloc[train]  
    full_test_predictions = []  
    for alg,predictors in algorithms:        
        alg.fit(titanic[predictors].iloc[train,:],train_target)    
        test_prediction = alg.predict_proba(titanic[predictors].iloc[test,:].astype(float))[:,1]  
        full_test_predictions.append(test_prediction)
    test_predictions = (full_test_predictions[0] + full_test_predictions[1]) / 2  
    test_predictions[test_predictions >.5] = 1  
    test_predictions[test_predictions <=.5] = 0        
    predictions.append(test_predictions)    
predictions = np.concatenate(predictions,axis=0)      
accury = sum(predictions == titanic['Survived']) / len(predictions)#测试准确率  
print(accury) 

#out  0.82379349046 

感觉这个结果很不可思议了，因为之前刚写好的时候是81%多点，还没单纯的用随机森林模型预测的准确率高，然后调节了一下参数，准确率达到82.3%
还算不错，不过还是有提升空间，但是仅通过调参已经不能再提高多少了，，所以就应该从特征工程上下手，将特征重要性排序，重要性不高的特征适当去掉，又或者衍生出更多比较重要的特征，这是提高准确率的最重要的方法。
另外，在CSDN找到的有关特征工程和k折交叉验证的博客
机器学习中的特征工程
http://blog.csdn.net/xiaodongxiexie/article/details/55830550
K折交叉验证
http://blog.csdn.net/light_blue_love/article/details/42004041
以及Kaggle入门系列
http://m.blog.csdn.net/u013115001/article/details/78012553