经典人脸识别算法小结——EigenFace, FisherFace & LBPH（下）

该文章由下面两部分组成：

1).经典人脸识别算法小结——EigenFace, FisherFace & LBPH（上），这部分介绍人脸开源库，和图片的读取等准备工作。

2).经典人脸识别算法小结——EigenFace, FisherFace & LBPH（下），这部分介绍三种人脸识别算法。

如果对于opencv中的人脸识别API感兴趣，可参看官方的说明：Face Recognition with OpenCV。

1.EigenFace

EigenFace(特征脸)在人脸识别历史上应该是具有里程碑式意义的，其被认为是第一种有效的人脸识别算法。1987年 Sirovich and Kirby 为了减少人脸图像的表示（降维）采用了PCA（主成分分析）的方法，1991年 Matthew Turk和Alex Pentland首次将PCA应用于人脸识别，即将原始图像投影到特征空间，得到一系列降维图像，取其主元表示人脸，因其主元有人脸的形状，估称为“特征脸”。

EigenFace是一种基于统计特征的方法，将人脸图像视为随机向量，并用统计方法辨别不同人脸特征模式。EigenFace的基本思想是，从统计的观点，寻找人脸图像分布的基本元素，即人脸图像样本集协方差矩阵的特征向量，以此近似的表征人脸图像，这些特征向量称为特脸。

下图对特征脸的应用进行了说明。从下图可以看出，一组特征脸基图像（特征脸1~d）组成一个特征脸子空间，任何一幅人脸图象（减去平均人脸后）都可投影到该子空间，得到一个权值向量(§1~d)。计算此向量和训练集中每个人的权值向量之间的欧式距离，取最小距离所对应的人脸图像的身份作为测试人脸图像的身份。而这里所提到的一组特征脸基图像（也就是特征脸，或者叫特征向量），正是利用PCA所求得的协方差矩阵的特征向量。具体可以参考主成分分析（PCA）和线性判别分析（LDA）原理简介。

EigenFace的工作流程如下所示，如果想要更具体的介绍可以参考：特征脸

下面代码是基于opencv的API，利用ORL的数据库来训练模型，并对test图像进行识别。为了更好的理解特征脸，下面也对第一幅图像进行了重建。

#include
#include
#include

using namespace std;
using namespace cv;
using namespace cv::face;

int main(void)
{
	//读取已经生成好的list.txt文件，关于list.txt文件的
	//生成请参考：经典人脸识别算法小结——EigenFace, FisherFace & LBPH（上）
	string fileName = string("D:/Opencv Picture/Face/list.txt");
	ifstream file(fileName.c_str(), ios::in);
	if (!file)
	{
		cout << "Load file ERR!" << '\n';
		return -1;
	}
	string line, path, classLabel;
	vector images;
	vector labels;
	char separater = ';';
	while (getline(file, line))
	{
		stringstream line_c(line);
		getline(line_c, path, separater);
		getline(line_c, classLabel);
		if (!path.empty() || !classLabel.empty())
		{
			Mat image = imread(path, 0);//读取灰度图像
			images.push_back(image);
			labels.push_back(atoi(classLabel.c_str()));
		}
	}

	if (images.size() < 1 || labels.size() < 1)
	{
		cout << " File Path ERR!" << '\n';
		return -1;
	}

	//将images中的最后一张图像作为test图像
	Mat testImg=images[images.size()-1];
	int test_label=labels[labels.size()-1];
	images.pop_back();
	labels.pop_back();

	//训练模型
	Ptr model = createEigenFaceRecognizer();
	//model->train(images, labels);
	//model->save("model.xml");
	model->load("model.xml");//对于已经训练好并保存的模型，可以直接调用

	//对testImg进行识别
	int predictLabel = model->predict(testImg);
	cout << "The test image label is " << predictLabel << '\n';

	//显示meanFace
	Mat mean = model->getMean();
	Mat meanFace = mean.reshape(1, testImg.rows);
	Mat meanFace_norm;
	if(meanFace.channels()==1)
		normalize(meanFace, meanFace_norm, 0, 255, NORM_MINMAX, CV_8UC1);
	else if(meanFace.channels()==3)
		normalize(meanFace, meanFace_norm, 0, 255, NORM_MINMAX, CV_8UC3);
	imshow("meanFace", meanFace_norm);

	//显示前10个eigenFace
	Mat eigenVectors = model->getEigenVectors();
	for (int i = 0; i < min(10, eigenVectors.cols); ++i)
	{
		Mat eigenFace,eigenFace_norm;
		Mat ev = eigenVectors.col(i).clone();
		eigenFace = ev.reshape(1, testImg.rows);

		if (eigenFace.channels() == 1)
			normalize(eigenFace, eigenFace_norm, 0, 255, NORM_MINMAX, CV_8UC1);
		else if (eigenFace.channels() == 3)
			normalize(eigenFace, eigenFace_norm, 0, 255, NORM_MINMAX, CV_8UC3);

		Mat colorFace;
		applyColorMap(eigenFace_norm,colorFace,COLORMAP_RAINBOW);//为了方便观察
		imshow("eigenFace "+to_string(i), colorFace);
	}

	//每隔15个eigenVector重建一副图像
	imshow("original", images[0]);
	for (int num = min(10, eigenVectors.cols); num < min(300, eigenVectors.cols); num+=15)
	{
		Mat evs = eigenVectors(Range::all(), Range(0, num));//提取eigenVectors的前num列数据
		Mat projection = LDA::subspaceProject(evs, mean, images[0].reshape(1,1));//重建第一幅图像
		Mat reconstraction = LDA::subspaceReconstruct(evs, mean, projection);

		//显示重建的图像
		Mat result = reconstraction.reshape(1, testImg.rows);
		Mat result_norm;

		if (result.channels() == 1)
			normalize(result, result_norm, 0, 255, NORM_MINMAX, CV_8UC1);
		else if (result.channels() == 3)
			normalize(result, result_norm, 0, 255, NORM_MINMAX, CV_8UC3);

		imshow("Rec_face " + to_string(num), result_norm);
	}

	cvWaitKey(0);
	return 0;
}

平均脸及前10个eigenFaces如下所示。

下面是第一幅图像的原图像，original和每隔15个特征向量进行重建后的效果图。很明显随着引入进来的特征向量越来越多，重建后的效果也越来越接近原图。

2. FisherFace

FisherFace 是一种基于LDA(全称Linear  Discriminant Analysis, 线性判别分析)的人脸识别算法，而LDA是Ronald Fisher于193年提出来的，所以LDA也被称作是Fisher Discriminant Analysis, 也正因为如此，该人脸识别算法被称为FisherFace。

关于LDA可以参考主成分分析（PCA）和线性判别分析（LDA）原理简介。LDA有和PCA相同的地方是，都有利用特征值排序找到主元的过程，但是不同的是PCA求的是协方差矩阵的特征值，而LDA是求的是一个更为复杂的矩阵的特征值（具体如下）。其中需要注意的是在求均值时，和PCA也是有所不同的，LDA对每个类别样本求均值，而PCA是对所有样本数据求均值，得到平均脸。

LDA的降维步骤如下：

如果用一句话来概括LDA的中心思想就是最大化类间距离，最小化类内距离。

由于LDA利用了类成员信息并抽取了一个特征向量集，该特征向量集强调的是不同人脸的差异而不是照明条件、人脸表情和方向的变化。因此，相比EigenFace（和谁比很重要），采用Fisherface方法对人脸进行识别对光照、人脸姿态的变化更不敏感，有助于提高识别效果。

在opencv中的调用类似于前面的EigenFace。只是得到的eigenvectors的维度不同（从400变为39），另外在重建的时候，由于FisherFace只关注各类目标间的不同特征，所以希望重建出原图像是不现实的。

训练模型：

Ptr model = createFisherFaceRecognizer();
	//model->train(images, labels);
	//model->save("model.xml");
	model->load("model.xml");//对于已经训练好并保存的模型，可以直接调用

图像重建

for (int num =0; num < min(10, eigenVectors.cols); ++num)
	{
		Mat evs = eigenVectors.col(num);
		Mat projection = LDA::subspaceProject(evs, mean, images[0].reshape(1, 1));//重建第一幅图像
		Mat reconstraction = LDA::subspaceReconstruct(evs, mean, projection);

		//显示重建的图像
		Mat result = reconstraction.reshape(1, testImg.rows);
		Mat result_norm;

		if (result.channels() == 1)
			normalize(result, result_norm, 0, 255, NORM_MINMAX, CV_8UC1);
		else if (result.channels() == 3)
			normalize(result, result_norm, 0, 255, NORM_MINMAX, CV_8UC3);

		imshow("Rec_face " + to_string(num), result_norm);
	}

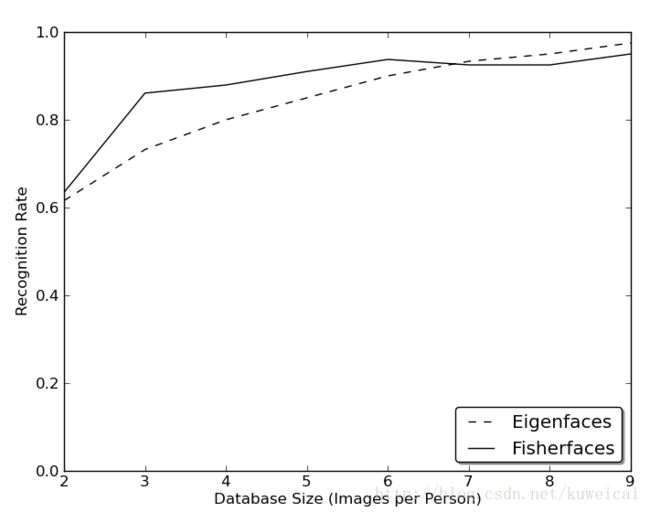
对于EigenFace 和 FisherFace，这两个方法的性能主要取决于输入数据，如果是左右偏转脑袋，可以容纳15°左右仍然保持较高的识别率，但是上下的偏转相对来说更敏感些。毕竟人脸是三维的，不是简单的旋转就能修复，稍微大一点的偏转最好还是通过3D建模来处理的。如果需要对光照有好的鲁棒性，可以考虑gabor和LBPH。

有分析显示，对于EigenFace和FisherFace，要想达到好的识别效果，每个样本对象至少要采集8副左右的图像。

3. LBPH

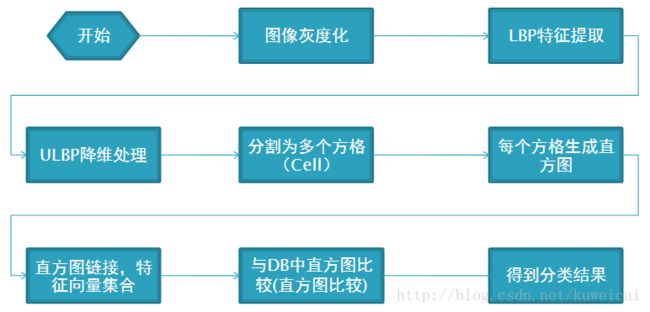
LBPH是利用局部二值模式直方图的人脸识别算法。关于LBP的原理可以参考：LBP小结：LBP及改进版本的原理和opencv实现源代码。

下面是其计算步骤：

LBP是典型的二值特征描述子，所以相比前面EigenFace和FisherFace，更多的是整数计算，而整数计算的优势是可以通过各种逻辑操作来进行优化，因此效率较高。另外通常光照对图中的物件带来的影响是全局的，也就是说照片中的物体明暗程度，是往同一个方向改变的，可能是变亮或变暗，只是改变的幅度会因为距离光源的远近而有所不同。所以基本上局部相邻(Local)的像素间，受光照影响后数值也许会改变，但相对大小不会改变，因此LBP特征对光照具有比较好的鲁棒性。

LBPH在opencv的API调用如下：

//训练模型
	Ptr model = createLBPHFaceRecognizer();
	model->train(images, labels);