FP-Growth算法介绍

FP-Growth算法介绍

参考了几篇文章关于FP-Growth的看法，融合一下，以供参考，如有转载侵权，请联系删除。

====================（1）转自：http://www.bjt.name/2013/09/association-rules/ 

关联规则（association rules）是一种广泛使用的模式识别方法，比如在购物篮分析（Market basket Analysis），网络连接分析（Web link），基因分析。我们常常提到的购物篮分析，它的典型的应用场景就是要找出被一起购买的商品集合。

关联规则的可能的应用场景有：

• 优化货架商品摆放，或优化邮寄商品目录的内容
• 交叉销售和捆绑销售
• 异常识别等

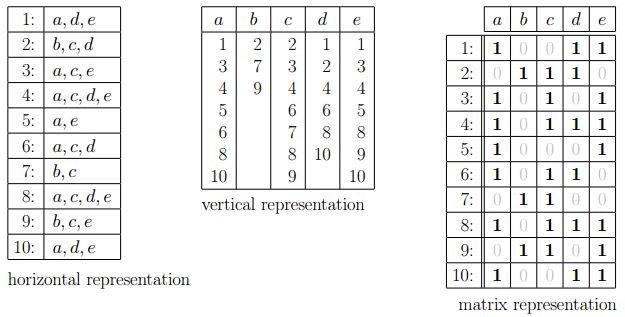
关于交易数据的表述形式

先说最简单的三种形式，水平表述、垂直表述和矩阵表述，直接看图：

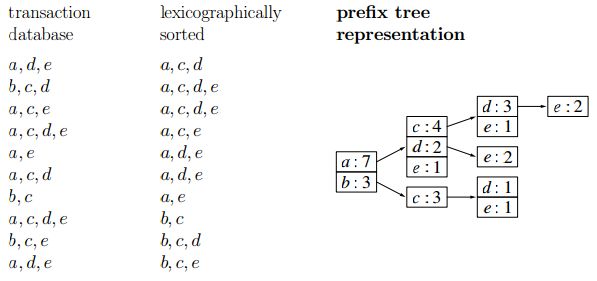
接着是稍稍变换之后的两种表述形式：

• 排序表述（lexicographically sorted）
• 前缀树表述（prefix tree）

这三种数据表述形式（水平、垂直、前缀树）分别对应算法：apriori、Eclat 和 FP growth，本篇主要描述 apriori 和 FP growth 两种算法。

Apriori 算法

Apriori算法是一种最有影响的挖掘 0-1 布尔关联规则频繁项集的算法。这种算法利用了频繁项集性质的先验知识（因此叫做priori）。Apriori使用了自底向上的实现方式（如果集合 I 不是频繁项集，那么包含 I 的更大的集合也不可能是频繁项集），k - 1 项集用于探索 k 项集。首先，找出频繁 1 项集的集合()，用于找频繁 2 项集的集合 ，而  用于找 ，如此下去，直到不能找到满足条件的频繁 k 项集。搜索每个  需要一次全表数据库扫描。

我们假设一个很小的交易库：{1,2,3,4}, {1,2}, {2,3,4}, {2,3}, {1,2,4}, {3,4}, {2,4}

首先我们先要计算发生频数（或者叫做support）

item	support
{1}	3
{2}	6
{3}	4
{4}	5

1项集的最低频数是3，我们姑且认为他们都是频繁的。因此我们找到1项集所有可能组合的pairs：

item	support
{1,2}	3
{1,3}	1
{1,4}	2
{2,3}	3
{2,4}	4
{3,4}	3

在这里，{1,3}, {1,4} 不满足support大于3的设定（一般support是3/(3 + 6 + 4 + 5)），因此还剩下的频繁项集是：

item	support
{1,2}	3
{2,3}	3
{2,4}	4
{3,4}	3

也就是说，包含{1,3}, {1,4}的项集也不可能是频繁的，这两条规则被prune掉了；只有{2,3,4} 是可能频繁的，但它的频数只有2，也不满足support条件，因此迭代停止。

但我们可以想象，这种算法虽然比遍历的方法要好很多，但其空间复杂度还是非常高的，尤其是  比较大时， 的数量会暴增。而且每次Apriori都要全表扫描数据库，开销也非常大。

即便如此 apriori 算法在很多场景下也足够用。在R语言中使用 arules 包来实现此算法（封装的是C实现，只要装载的 sparse matrix 可以载入内存，support 设置合理，速度非常快）。

FP growth

前文提到了用apriori需要全表扫描，对于超大型数据会出现一些问题。如果有一种方法，可以不每次全表扫描，而是用一个简洁的数据结构（压缩之后的数据库）把整个数据库的信息都包含进去，通过对数据结构的递归就完成整个频繁模式的挖掘，并保证最低的搜索消耗。这种方法的其中一种实现便是 FP growth算法。这个算法因为数据结构的 size 远远小于原始的数据库，所有的数据操作可以完全在内存中计算，挖掘速度就可以大大提高。

FP growth 算法包含两部分：存储的FP tree 和对应的FP 算法：

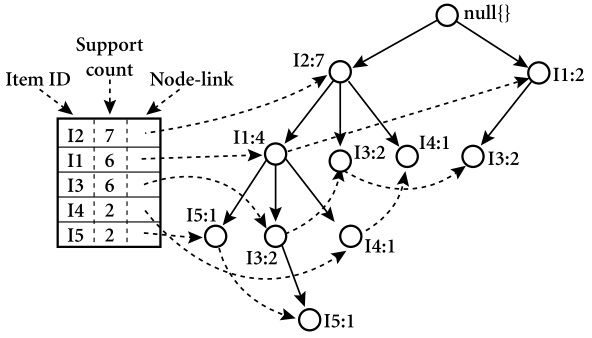
FP-tree 的结构

想想开头提到的交易数据的前缀树表述，那是一种压缩数据的方法。J. Han 对 FP-tree 的定义如下：

1. 根节点被标记为 root，item 按照一定的顺序连接为子树。以及一个frequent-item-header 表（其实就是item按照出现频率排序的表格，下图中左侧的表格）
2. 每个子树上包含如下信息：
   • item 的名称（比如下图中I2, I3, I5等）
   • 计数（support count）：到达这个节点的路径深度
   • 节点的连接情况（node-link，和哪个节点有关系）

FP-tee 的算法

我们拿一个例子来说明问题。假如我们数据库中记录的交易信息如下（最低support为3）：

No.	transactions	Sort
1	ABDE	BEAD
2	BCE	BEC
3	ABDE	BEAD
4	ABCE	BEAC
5	ABCDE	BEACD
6	BCD	BCD

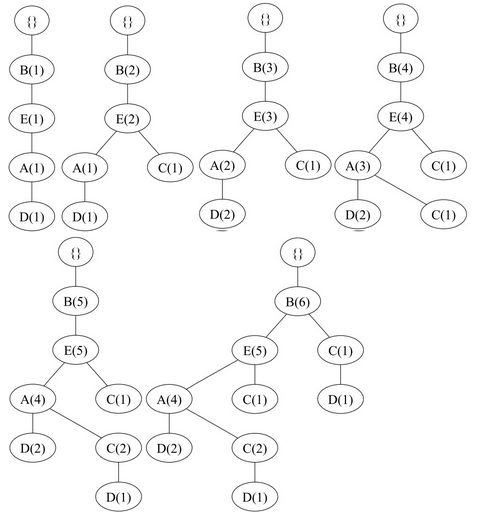
首先我们先要了解所有的一项集出现的频率（support，重新排序的结果见上图的Sort部分）：B(6), E(5), A(4), C(4), D(4)。

对于排序后的每条记录的迭代后 FP-tree 结构变化过程为（也就是一条一条计数的增加）：

也就是说，原始数据被压缩到和最后那张图一样的结构上。

接着是比较关键的 FP-tree 的挖掘，过程见下图：

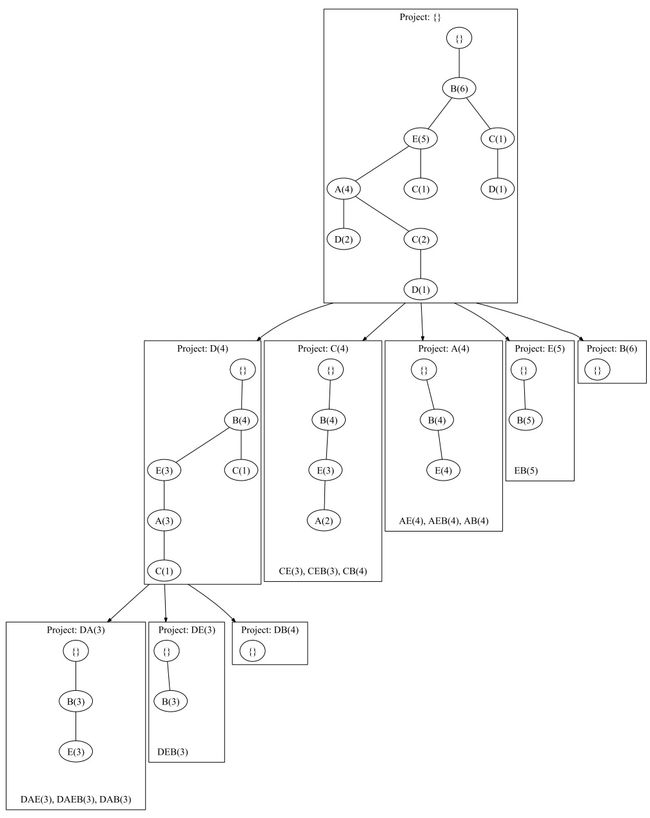
对于D这个节点来说，首先它的频繁项集是 ，它包含在三条链路里：

第一条链路里D有两次出现，而其他两个链路在D的条件下各出现了一次。因此我们说D有3个前缀路径

根据这个信息我们重构D条件下的 FP-tee，则如下图中  的结构。当然还没有完，还要继续搜索可能的规则，因为我们的 support 为3，因此  中，最末端的两个  则应该减枝掉。而A、E、B的频数依然可以被使用，即 。

• 对于  的前缀路径是  的树形结构，因此这条线的最终结果是 。
• 对于  的前缀路径是  的属性结构，最终结果是 
• 对于  只有一个根，没有结果

对于C这个节点来说，同样可以找到它的前缀路径 ，因此得到  的结构，A被减枝掉，则最后剩余了 。

再向上，找A节点；找E节点；找B节点；这样一步一步搜索所有可能的结果。最终满足support大于3条件的频繁项集即为 

当然，上面只是简单的把 FP-tree 的原理说明了一下，里面的一些trick并没有提及，感兴趣的读者可以找一找相关paper。

FP-tree 算法在R中的实现

在R中没有现成的包来做这个事情，但有意思的是arules包的作者也写了 FP-tree 算法，只是没有封装而已。当然只要有算法的C代码，嵌入到R环境中也是不难的。

先到作者的主页下载相关的源代码，我选择是的fpgrowth.zip的C代码编译通过。

1. cd /home/liusizhe/download/fpgrowth/fpgrowth/src/
2. make
3. make install
4. ./fpgrowth -m2 -n5 -s0 .075 /home/liusizhe/experiment/census.dat frequent

参数的话，可以直接参考 fpgrowth 的帮助，比如上面m对应的是最小项集，n对应的最大项集，s是support值，后面接了 inputfile 和 outputfile 两个文件。

---

当然，如果有必要的话，上面的算法都可以写到并行架构，比如 map-reduce。甚至如果只是求解二项集，在不同的语言环境下甚至几行代码就可以搞定。

参考目录和延伸阅读：

• http://en.wikipedia.org/wiki/Association_rule_learning
• http://en.wikipedia.org/wiki/Apriori_algorithm
• http://www.borgelt.net//courses.html#fpm

==================(2)

Apriori算法的优点：简单，易操作。缺点：计算量大，重复scan数据库。
FP growth算法的优点：计算量小，可以寻根溯源。缺点：容易出现树形矮扁的状况。

=====================(3) 转自：http://blog.csdn.net/mangoer_ys/article/details/43370633

频繁项集挖掘是一个关联式规则挖掘问题。关联挖掘是数据挖掘中研究最早也是最活跃的领域，其中频繁模式的挖掘是关联挖掘的核心和基础，是产生关联规则挖掘的基础。频繁项集最经典的应用就是超市的购物篮分析。

首先要理解频繁项集中的以下概念。

       频繁项：在多个集合中，频繁出现的元素项。

       频繁项集：在一系列集合中每项都含有某些相同的元素，这些元素形成一个子集，满足一定阀值就是频繁项集。

       K项集：K个频繁项组成的一个集合。

       支持度：包含频繁项集（F）的集合的数目。

       可信度：频繁项与某项的并集的支持度与频繁项集支持度的比值。

      简单来说。频繁项集的挖掘就是将数据集（一般是多行数据，每行数据的第一个元素的交易编号，后面的是物品编号）中出现频率超过支持度的频繁项找出来，而首先找出的单个频繁项的集合就是1-频繁项集。而2-频繁项就是某两个频繁项都同时出现在一行中并且出现频率超过支持度的，那么2-频繁项集就是这些2-频繁项的集合，依次类推，K-频繁项集就是K-频繁项的集合。

      目前针对频繁项集的算法，主要有Apriori，FP-Growth和Eclat算法。

Aporiori

       首先来了解一下Apriori算法的思路：Apriori算法需要对数据集进行多步处理。第一步，统计所有含一个元素项目集出现的频数，并找出那些不小于最小支持度的项目集即1-频繁项集，从第二部开始循环处理直到再没有频繁项集生成。循环过程是：第K步中，根据K-1步生成的（K-1）维频繁项集产生K候选项目集，然后对数据及进行搜索，得到候选项目集的项集支持度，与最小支持度进行对比，从而得到K-频繁项集。

FP-Grwoth

       Apriori算法虽然思路很简单，但是该算法有以下缺点：(1)在每一步产生侯选项目集时循环产生的组合过多，没有排除不应该参与组合的元素;(2)每次计算项集的支持度时，都对数据集中的全部记录进行了一遍扫描比较，

由于本题中数据集较大，这样扫描下来会大大增加计算机的IO开销。这种代价会让计算机奔溃。

针对Apriori算法的性能瓶颈——需要产生大量候选集和需要重复扫描数据集，FP-growth算法应用而生。该算法只进行2次数据集扫描而且不使用候选集，直接压缩数据集成一个频繁模式树（FP树），最后通过这个FP树生成频繁项集。对于本题较大的数据集，FP-growth算法是个不错的选择。

那么首先需要理解FP树的结构和建树过程。

表1

交易ID	物品ID	过滤后
01	a b c e f h i k	a b c
02	b e g j m o s	e j
03	a e h j s	a e j
04	a c	a c
05	a b c j l p	a b c j
06	b e f m n o	b e

假设最小支持度是40%，那么b e j c的支持度就是50%，a是67%。过滤掉非频繁项集后即如上表中最后一列。并使这些元素按照出现的次序排序。

表2

元素	支持度
a	67%
b	50%
c	50%
e	50%
j	50%

这一步其实就是预处理，减少需要计算的频繁项集的候选集，排序的目的是频繁项集关注的是组合而不是排列，在后面生成树的时候需要避免生成重复不必要的分支。

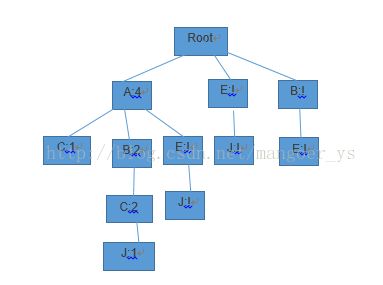
然后遍历过滤后的候选集和出现的次序，构建FP-tree如下。

图1

   

      发现频繁项集的过程和Apriori一样，也是逐步递增的发现，即先找到1频繁项集，然后再在1频繁项集的基础上找2频繁项集。基于上面的FP-tree树，其实已经找到了1频繁项集，即表2中的所有元素。

在找2频繁项集时，需要先抽取条件模式基（以每个频繁项为结尾的，在FP树中所有的前缀路径）

表3

频繁项	条件模式基
A	{}:4
B	{A}:2
C	{A}:1,{A,B}:2,
E	{A}:1,{}:1,{B}:1
J	{A,B,C}:1,{A,E}:1,{E}:1

 

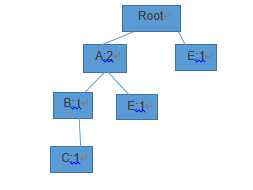
       然后对于表3中的频繁项集元素，用它的条件模式基建立FP树，再找2频繁项集。

如图2为j的FP树

图2

   

        建树的过程和上面是一样的，然后再得到2频繁项集。依次类推，挖掘K频繁项集只需要在K-1频繁项集上挖掘，重复上面的过程即可。

        从这里就可以发现一旦建立了FP树之后就可以不断递归挖掘K频繁项集，对于Hadoop就会产生多次IO操作，严重影响程序运行效率，而Spark这种弹性式内存计算框架可以试中间输出和结果保存在内存中，不需要重复读写HDFS，所以Spark能更好地适用于数据挖掘需要递归的Map-Reduce算法。

Spark下FP-Growth

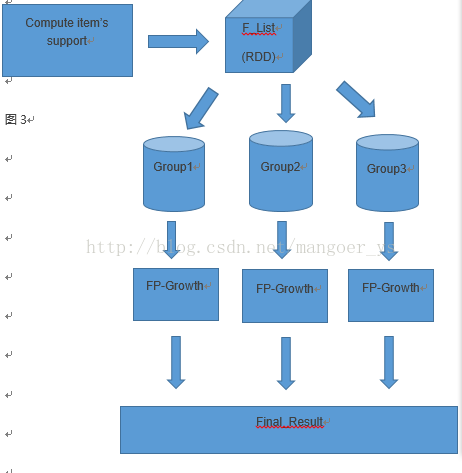
        在spark下部署FP-growth算法的主要思路分为五步，涉及三步MR。（流程图见图3）

        第一步：计算F_list，也就是计算所有item的support，这一步可以通过ＭＤ得到，实质和WordCount一样。

        第二步：数据分组，将F_list中的条目分成G个组，就形成了一个Group_list，这其中每一个Group都包含一组item的集合。

        第三步：并行执行FP-growth，这步和上面所说的普通FP-growth是一样的，只是需要MR来完成。这一步中mapper完成的主要功能是数据集分区，逐个处理数据分区中的事务，将事务分为item，每个item根据Group_list映射到合适的group中去，然后在reduce中并行执行FP-growth算法。

        第四步：聚合，这一步将各台机器上的结果聚合成最终的结果。这一步也需要MR来完成，将各台机器上的频繁项集聚合在一起，并计算支持度。

 图3

算法实现

          算法实现同样也分为四步（详细注释见源代码）：

（1）   计算每个item的支持度。

val f = file.map(line => (line.split(" ") .drop(1) .toList.sortWith(_ < _), 1)  .reduceByKey(_ + _)

在计算支持度之前先将重复的行合并重复行并删除事务编号（每行第一个为事务编号）。

 

 

计算支持度并保存在内存中。

 

val g = f.flatMap(line => {       var l = List[(String, Int)]()       for (i <- line._1) {         l = (i, line._2) :: l       }       l     }).reduceByKey(_ + _) .sortBy(_._2, false) .cache()

（2）   数据分组

其中g_size是分组的个数。item是数据集中事务和出现次数的键值对。将item中数据分成g_size个组，将相关的数据分成一组，每个group中都包含一组item。

val f_list = item.flatMap(t => {       var pre = -1       var i = t._1.length - 1       var result = List[(Int, (List[Int], Int))]()       while (i >= 0) {         if ((t._1(i) - 1) / g_size != pre) {           pre = (t._1(i) - 1) / g_size           result = (pre, (t._1.dropRight(t._1.length - i - 1), t._2)) :: result         }         i -= 1       }       result     })       .groupByKey()       .cache()

（3）   并行化执行FP-Growth

其中fp_growth是一个fp树的函数，其中主要包含建树，前缀处理，单支处理和挖掘频繁项。

val d_result = f_list.flatMap(t => {    fp_growth(t._2, support_num, t._1 * g_size + 1 to (((t._1 + 1) * g_size) min g_count)) })

（4）   合并结果

d_result中包含了所有数据分组的频繁项集，这一步将所有的频繁项集合并，并将结果转换为要求的数据格式。

val temp_result = d_result.map(t => (t._1.map(a => g_list(a - 1)._1), t._2)) val result = temp_result.map( t => ( listToString(t._1)._2, listToString(t._1)._1 + ":" + t._2.toFloat/line_num.toFloat ) ) .groupBy(_._1)

  代码

import org.apache.spark.SparkConf
import org.apache.spark.SparkContext
import org.apache.spark.SparkContext.rddToPairRDDFunctions
import scala.collection.mutable.Map
import scala.tools.ant.sabbus.Break

object FP_Growth {

  def main(args: Array[String]) = {
    val support_percent = 0.85
    val pnum = 32
    val conf = new SparkConf()
    val sc = new SparkContext(conf)
    val file = sc.textFile(args(0))
    val line_num = file.count()

    //remove the repeat line
    //line key:transcationID
    //line value:itemIDs
    val f = file.map(line => (
      line.split(" ")
      .drop(1)
      .toList
      .sortWith(_ < _), 1))
      .reduceByKey(_ + _)


    //compute support rate of every item
    //line key:itemIDs
    //line value:the number of line appear
    //g's element key:itemID
    //g's element value:support rate of every item
    val g = f.flatMap(line => {
      var l = List[(String, Int)]()
      for (i <- line._1) {
        l = (i, line._2) :: l
      }
      l
    })
      .reduceByKey(_ + _)
      .sortBy(_._2, false) //disascend sort
      .cache() //persist this RDD with the default storage level

    //convert g to a array
    val g_list = g.collect.toArray

    //the number of g_list' item
    var g_count = 0
    //convert g_list to a map
    //g_map's element key : itemID
    //g_map's element value : serial number
    val g_map = Map[String, Int]()

    //number for the itemID
    for (i <- g_list) {
      g_count = g_count + 1
      g_map(i._1) = g_count
    }

    //compute the number of serial items
    //t key:itemIDs
    //t value:the number of line appear
    //item's element key : the serial numbers of item
    //item's element value : the number of item appear
    val item = f.map(t => {
      var l = List[Int]()
      for (i <- t._1)
        l = g_map(i) :: l
      (l.sortWith(_ < _), t._2)
    })

    //======================================
    //compute the min_support rating
    val support_num: Int = item.map(t => (1, t._2))
      .reduceByKey(_ + _)
      .first()._2 * support_percent toInt

    val g_size = (g_count + pnum - 1) / pnum
    //divide items into groups
    //t key : the serial numbers of item
    //t value : the number of item appear
    //f_list's element key : groupID
    //f_list's element value : the prefix items and corresponding number of the group
    val f_list = item.flatMap(t => {
      var pre = -1
      var i = t._1.length - 1
      var result = List[(Int, (List[Int], Int))]()
      while (i >= 0) {
        if ((t._1(i) - 1) / g_size != pre) {
          pre = (t._1(i) - 1) / g_size
          result = (pre, (t._1.dropRight(t._1.length - i - 1), t._2)) :: result
        }
        i -= 1
      }
      result
    })
      .groupByKey()
      .cache()

    //parallelize FP-Growth
    //t key : groupID
    //t value : the prefix items and corresponding number of the group
    //d_result's element key : frequent itemset
    //d_result's element value : the number of frequent itemset appear
    val d_result = f_list.flatMap(t => {
      fp_growth(t._2, support_num, t._1 * g_size + 1 to (((t._1 + 1) * g_size) min g_count))
    })

    //save result into required format
    val temp_result = d_result.map(t => (t._1.map(a => g_list(a - 1)._1), t._2))
    val result = temp_result.map( t => ( listToString(t._1)._2, listToString(t._1)._1 + ":" + t._2.toFloat/line_num.toFloat ) ).groupBy(_._1)
    result.map(t => t._2.map(s => s._2)).saveAsTextFile(args(1))

    sc.stop()
  }

  //convert list to string
  def listToString(l: List[String]): (String, Int) = {
    var str = ""
    var count = 0
    for (i <- l) {
      str += i + ","
      count += 1
    }
    str = "\r\n" + str.substring(0, str.size - 1)
    return (str, count)
  }
  /**
  /* fp-tree' growth
  /* contains make tree,prefix cut,deal with target,deal with single branche and mining frequent itemset
  **/
  def fp_growth(v: Iterable[(List[Int], Int)], min_support: Int, target: Iterable[Int] = null): List[(List[Int], Int)] = {
    val root = new tree(null, null, 0)
    val tab = Map[Int, tree]()
    val tabc = Map[Int, Int]()
    //make tree
    for (i <- v) {
      var cur = root;
      var s: tree = null
      var list = i._1
      while (!list.isEmpty) {
        if (!tab.exists(_._1 == list(0))) {
          tab(list(0)) = null
        }
        if (!cur.son.exists(_._1 == list(0))) {
          s = new tree(cur, tab(list(0)), list(0))
          tab(list(0)) = s
          cur.son(list(0)) = s
        } else {
          s = cur.son(list(0))
        }
        s.support += i._2
        cur = s
        list = list.drop(1)

      }
    }
    //prefix cut
    for (i <- tab.keys) {
      var count = 0
      var cur = tab(i)
      while (cur != null) {
        count += cur.support
        cur = cur.Gnext
      }
      //modify
      tabc(i) = count
      if (count < min_support) {
        var cur = tab(i)
        while (cur != null) {
          var s = cur.Gnext
          cur.Gparent.son.remove(cur.Gv)
          cur = s
        }
        tab.remove(i)
      }
    }
    //deal with target
    var r = List[(List[Int], Int)]()
    var tail: Iterable[Int] = null
    if (target == null)
      tail = tab.keys
    else {
      tail = target.filter(a => tab.exists(b => b._1 == a))
    }
    if (tail.count(t => true) == 0)
      return r
    //deal with the single branch
    var cur = root
    var c = 1
    while (c < 2) {
      c = cur.son.count(t => true)
      if (c == 0) {
        var res = List[(Int, Int)]()
        while (cur != root) {
          res = (cur.Gv, cur.support) :: res
          cur = cur.Gparent
        }

        val part = res.partition(t1 => tail.exists(t2 => t1._1 == t2))
        val p1 = gen(part._1)
        if (part._2.length == 0)
          return p1
        else
          return decare(p1, gen(part._2)) ::: p1
      }
      cur = cur.son.values.head
    }
    //mining the frequent itemset
    for (i <- tail) {
      var result = List[(List[Int], Int)]()
      var cur = tab(i)
      while (cur != null) {
        var item = List[Int]()
        var s = cur.Gparent
        while (s != root) {
          item = s.Gv :: item
          s = s.Gparent
        }
        result = (item, cur.support) :: result
        cur = cur.Gnext
      }
      r = (List(i), tabc(i)) :: fp_growth(result, min_support).map(t => (i :: t._1, t._2)) ::: r

    }
    r
  }

  def gen(tab: List[(Int, Int)]): List[(List[Int], Int)] = {
    if (tab.length == 1) {
      return List((List(tab(0)._1), tab(0)._2))
    }
    val sp = tab(0)
    val t = gen(tab.drop(1))
    return (List(sp._1), sp._2) :: t.map(s => (sp._1 :: s._1, s._2 min sp._2)) ::: t
    //TODO: sp._2 may not be min
  }

  //笛卡尔积
  def decare[T](a: List[(List[T], Int)], b: List[(List[T], Int)]): List[(List[T], Int)] = {
    var res = List[(List[T], Int)]()
    for (i <- a)
      for (j <- b)
        res = (i._1 ::: j._1, i._2 min j._2) :: res
    res
  }
}

class tree(parent: tree, next: tree, v: Int) {
  val son = Map[Int, tree]()
  var support = 0
  def Gparent = parent
  def Gv = v
  def Gnext = next
}