风格迁移学习之《Deep Painterly Harmonization》论文笔记
简介
关于风格迁移的课题,近些年出现了不少文章,也取得了不错的效果。但是大多数研究都是整幅图像的风格迁移。《Deep Painterly Harmonization》这篇文章创造性地提出了一种基于风格迁移的图像融合方法,可以将一幅图像毫无违和感地嵌入另一幅图像当中。论文中的效果图如下图所示。该算法经过两个步骤,将直接嵌入的图像融合到风格图像当中,对嵌入的图像进行了风格转换。
论文作者开源了论文的代码,https://github.com/luanfujun/deep-painterly-harmonization。博主很早就想详读一下论文并跑一下源码。然而代码由lua语言和torch框架编写,语言和框架都不是很熟悉。这几天正好有时间,装好了整个环境,不熟悉Lua和torch想跑一下代码的童鞋可以移步这篇博客“ Ubuntu16.04 + troch + cuda + deep-painterly-harmonization测试记录”。配环境有几个坑,第一,代码必须用LUA5.1的环境,所以torch安装时要用TORCH_LUA_VERSION=LUA51 ./install.sh。第二,安装torch前加上一句话,export TORCH_NVCC_FLAGS="-D__CUDA_NO_HALF_OPERATORS__"。这篇博客将主要讲述论文的方法原理。
损失函数
为了实现无违和的图像融合,文章中使用了多种loss函数。在对文章方法进行讲述之前,我们首先要搞懂这几种loss函数。
Style and Content Losses
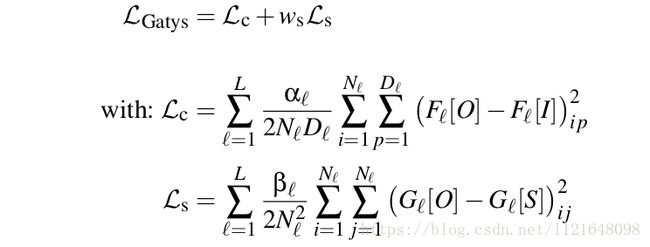
其中 L c \mathcal{L}_c Lc是内容损失, L s \mathcal{L}_s Ls是风格损失,由Gatys等在【2】中提出。其主要思想是图像的风格内容之间的差别可以由其经过深度神经网络后的激活值的差别来进行衡量。深度神经网络一般使用VGG网络。公式中, O O O为输出的融合图像, I I I为内容图像(此处内容图像即为输入图像), S S S为风格图像。 F l F_l Fl为第 l l l层的输出(激活值), G l G_l Gl为对应输出层的Gram矩阵。(GRAM矩阵可以看这里风格迁移(1)-格拉姆矩阵)
Histogram Loss
直方图损失在【3】中被首次提及,为了解决内容风格损失的不稳定问题。如下图所示,左右两幅图其实有着相同的gram矩阵。
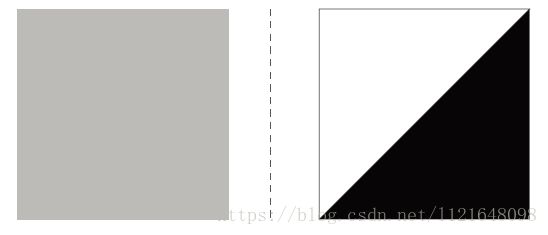
直方图损失的定义如下。
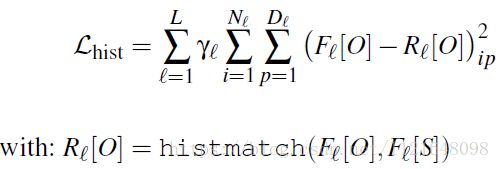
由公式可以看出,计算直方图损失,即首先计算输入图像的激活值以风格图像激活值为模板的直方图匹配(规定化),得到 R l [ O ] R_l[O] Rl[O]。再计算 F l [ O ] F_l[O] Fl[O]和 R l [ O ] R_l[O] Rl[O]之间的Frobenius 范数的平方。直方图规定化是数字图像处理的一个基本操作,不熟悉的童鞋看这里直方图规定化(直方图匹配)。Frobenius 范数很简单,就是指矩阵各项元素的绝对值平方的总和。
∣ ∣ X ∣ ∣ F 2 = ∑ i = 1 m ∑ j = 1 n ∣ x i , j ∣ 2 ||X||_F^2=\sum_{i=1}^m{\sum_{j=1}^n{|x_{i,j}|^2}} ∣∣X∣∣F2=i=1∑mj=1∑n∣xi,j∣2
Total Variation Loss
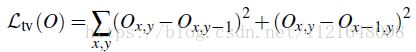
这一项loss对输出图片的变化进行了限制,【4】中的研究表明这一loss的加入可以使得输出结果更加平滑。
算法原理
首先对算法的原理进行一个概括。算法采用了与【2】中相同的迭代思想(要理解这篇文章得先理解【2】),将图像输入到VGG网络中,利用风格内容损失等方法产生损失,再将误差传递到输入层,输入层根据误差进行迭代。经过多次迭代,可以得到需要的风格和内容。和【2】中不同的是,这篇文章的专注于局部的风格转换,也就是说只对需要嵌入的图像进行迭代,而输入图像的其他部分不做任何改变。如下图所示,算法将仅仅对Input图像中在Mask图中标记的位置进行迭代。

在实现上,在loss的反向传播过程中,每一个尺度的feature map都会对应一个mask图像,即mask图像在传播过程中通过差值减小尺寸。文章的思想是在计算loss的时候,不管是content loss、style loss、histogram loss或者是tv loss,都只计算在mask中标记部分的loss。
第一步:高鲁棒性的初步融合
在这一步骤中,作者只使用了content loss和style loss。作者在编写loss函数时继承了torch.nn.Module并重写了反向传播。比如对Content loss的定义。代码中36行处,将反向传播loss与该层对应的mask图像相乘,这里是关键。
-- Define an nn Module to compute content loss in-place
local ContentLoss, parent = torch.class('nn.ContentLoss', 'nn.Module')
function ContentLoss:__init(strength, target, normalize, mask)
parent.__init(self)
self.strength = strength
self.target = target
self.normalize = normalize or false
self.loss = 0
self.crit = nn.MSECriterion()
self.mask = mask:clone()
end
function ContentLoss:updateOutput(input)
if input:nElement() == self.target:nElement() then
self.loss = self.crit:forward(input, self.target) * self.strength
else
print('WARNING: Skipping content loss')
end
self.output = input
return self.output
end
function ContentLoss:updateGradInput(input, gradOutput)
if input:nElement() == self.target:nElement() then
self.gradInput = self.crit:backward(input, self.target)
end
if self.normalize then
self.gradInput:div(torch.norm(self.gradInput, 1) + 1e-8)
end
self.gradInput:mul(self.strength)
self.gradInput:add(gradOutput)
local msk = self.mask:clone():repeatTensor(1,1,1):expandAs(input):cuda()
self.gradInput:cmul(msk)
return self.gradInput
end
对于style loss,作者仍然采取只对局部图像生成loss的思想,然而原始的style loss基于全局的gram矩阵,无法构建局部的loss,因此作者采用了类似于【5】的做法,将特征图分成小块进行匹配。作者将特征图分成3*3的小块,采取最邻近匹配的策略,即Input image的特征图中的一个patch对应style image特征图中对应位置的patch。分别计算这些patch的gram矩阵以构建style loss。
第二步:高质量精修
这一步与上一步的操作类似,只不过又添了Histogram Loss和TV loss两个loss进去,总的loss如下。
![]()
其中Histogram Loss和TV loss同样遵循构建局部loss的思想,仅仅在mask标记内的激活值可以产生loss。
参考文献
【1】Luan, Fujun, et al. “Deep Painterly Harmonization.” arXiv preprint arXiv:1804.03189 (2018).
【2】Gatys, Leon A., Alexander S. Ecker, and Matthias Bethge. “Image style transfer using convolutional neural networks.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016.
【3】Risser, Eric, Pierre Wilmot, and Connelly Barnes. “Stable and controllable neural texture synthesis and style transfer using histogram losses.” arXiv preprint arXiv:1701.08893 (2017).
【4】Johnson, Justin, Alexandre Alahi, and Li Fei-Fei. “Perceptual losses for real-time style transfer and super-resolution.” European Conference on Computer Vision. Springer, Cham, 2016.
【5】Li, Chuan, and Michael Wand. “Combining markov random fields and convolutional neural networks for image synthesis.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016.