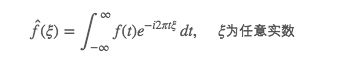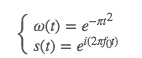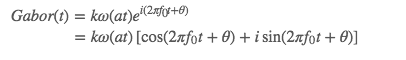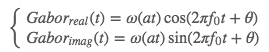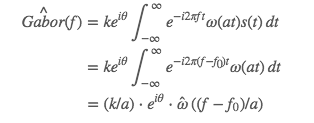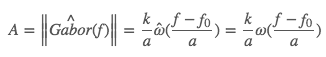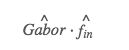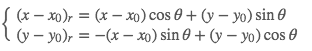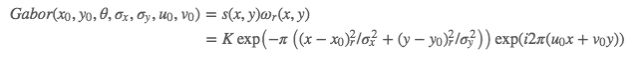原创|从傅立叶变换到Gabor滤波器
作者：夏 敏
编辑：李文臣
PART
01 gabor介绍
gabor特征
首先我们介绍下Gabor 特征，它是一种可以用来描述图像纹理信息的特征，Gabor 滤波器的频率和方向与人类的视觉系统类似，特别适合于纹理表示与判别。它主要依靠 Gabor 核在频率域上对信号进行加窗，从而能描述信号的局部频率信息。
而Gabor 核靠傅里叶变换，我们才能将信号转换到频率域，才能让Gabor核在频率域去加窗。而在原本的空间域中，一个 Gabor 核实际上就是一个高斯核与正弦波调制的结果，可以看做是高斯核应用在了正弦波的频域部分。
1
傅里叶变换傅里叶变换是一个线性的积分变换，从时域到频域，傅立叶变换分为连续傅立叶变换、傅立叶级数、离散时域傅立叶变换、离散傅立叶变换（DFT）.原理即是将输入的长度为N信号分解为N/2+1 正余弦，通过正交的原理。
傅里叶变换，实际上就是给一个时域的函数f(t)乘上旋转因子e^{-iwt}，然后在全时间域上积分。在全时间域上积分，所以最后结果就刨去了时间t的影响。最后的积分结果是一个只关于W的函数,也就是说是一个关于角频率的函数。这样就实现了时域到频域的转换。
通过傅里叶变换，我们能将任何波分解为不同频率波的叠加。这样转换的好处是：有些情况下空域中很复杂的问题，在频率域会变得十分简单。
时间域中的一个正弦波波形，在频率域中只要一个点就能表示
2
一维Gabor核一维傅里叶变化定义如下：
其中，f 为输入信号，ξξ 表示分解得到的各个波的频率，f̂ (f,ξ)f^(f,ξ) 为变换后的信号。公式中的 e−i2πxξe−i2πxξ 表示一个复数波
一维 Gabor 核
一维Gabor核由一个高斯核与一个复数波的乘积定义：
其中，
将复数波s(t)=ei(2πf0t)s(t)=ei(2πf0t)代入式中，得到：
上面最后一步得到了 Gabor 核的复数表示，我们就可以按实部和虚部将其拆分为实核和虚核，在很多应用中，我们只需要应用 Gabor核的实数部分即可：
Gabor 核的傅里叶变换
将 Gabor 核套入一维傅里叶变换中，得到 Gabor 核的傅里叶变换
上式中出现了 ω̂ (f−f0/a) 的形式，这里需要补充高斯核一个很有趣的性质：ω̂ (f)=ω(f)=e^−πf^2。根据这个性质，上式中的 ω̂ (f−f0/a)也可以写作 ω(f−f0/a)，二者可以自由转换。
Gabor核傅里叶变换后是这样一个形式：
这个形式可以看做是一个复数波，它的幅度
Gabor核相当于在频率域应用了一个高斯核窗口。假设我们这时有了一个信号的频率域：fin(f)，那么我们直接用频率域的Gabor核 Gabor^ 与其相乘，就实现了对 f0 频率邻域范围内的滤波效果：输入信号频率离这个 Gabor 核的 f0 越远，则乘上Gabor核之后的结果就越小，尤其是当 fin 在 f0 的 3σ 区间外时，这个频率几乎可以忽略不计。于是，最终能保留下来的信号就都是 f0频率附近的信号了。
滤波公式：
给我们任意一个输入信号，我们先用傅里叶变换将其变换到频率域得到fin^，再用 Gabor 核的傅里叶变换结果与之相乘，就是频域滤波的结果了。
不过我们大可不必这么麻烦，因为有卷积定理：
gabor特征：
用 Gabor 核和输入信号卷积就可以得到输入信号在某频率邻域附近的响应结果
响应结果来实现频域滤波，又可以用它来描述信号的频率信息。Gabor特征就是用Gabor核来描述信号的频率信息，从而作为信号的特征的。
3
二维Gabor核二维复数波
于初始相位对Gabor核影响不大，因此可以将其省略
二维高斯函数
考虑全面的话，高斯函数还要有（顺时针）旋转
所以，
二维的Gabor核
二维高斯函数与二维复数波相乘
各个参数含义如下：
(x0,y0): 高斯核的中心点
θ: 高斯核的旋转方向（顺时针）
(σx,σy): 高斯核两个方向上的尺度
(u0,v0): 频域坐标
K: 高斯核的幅度（magnitude）的比例
4
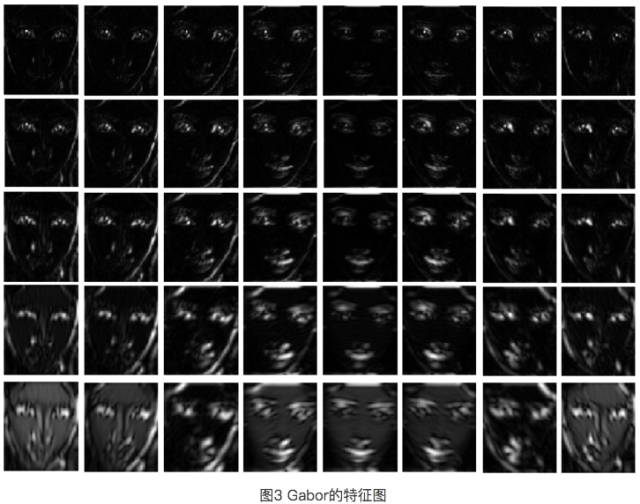
Gabor核作为图像特征一个Gabor核能获取到图像某个频率邻域的响应情况，这个响应结果可以看做是图像的一个特征。那么，我们如果用多个不同频率的Gabor核去获取图像在不同频率邻域的响应情况，最后就能形成图像在各个频率段的特征，这个特征就可以描述图像的频率信息了
上图展示了一系列具有不同频率的 Gabor 核，用这些核与图像卷积，我们就能得到图像上每个点和其附近区域的频率分布情况。
PART
02 gabor滤波器
介绍
通常有8个方向，5个尺度
从图1a和图2a可以清楚看出，每一列为尺度变化，一共有5个尺度。每一行为方向变化，一共有五个方向。
例子
把人脸图像分别用对应的实部虚部滤波器进行滤波，再进行平方相加开根号。就可以得到人脸的Gabor特征了，如图2待提取的人脸图像
优化
这个特征太大！（1）不适合存储。（2）有很多不需要的特征，导致维数灾难。
一种特征降维的方法，称为pooling池化，
1）对特征图可以进行max pooling ｜ mean polling |Stochastic-pooling
mean-pooling
即对邻域内特征点只求平均：假设pooling的窗大小是2x2, 在forward的时候，就是在前面卷积完的输出上依次不重合的取2x2的窗平均，得到一个值就是当前mean pooling之后的值。backward的时候，把一个值分成四等分放到前面2x2的格子里面就好了。举例：
forward: [1 3; 2 2] -> [2]backward: [2] -> [0.5 0.5; 0.5 0.5]
max-pooling
即对邻域内特征点取最大。forward的时候你只需要把2x2窗子里面那个最大的拿走就好了，backward的时候你要把当前的值放到之前那个最大的位置，其他的三个位置都弄成0。举例：
forward: [1 3; 2 2] -> 3backward: [3] -> [0 3; 0 0]
Stochastic-pooling
通过对像素点按照数值大小赋予概率，再按照概率进行亚采样，在平均意义上，与mean-pooling近似，在局部意义上，则服从max-pooling的准则
只需对feature map中的元素按照其概率值大小随机选择，即元素值大的被选中的概率也大。而不像max-pooling那样，永远只取那个最大值元素
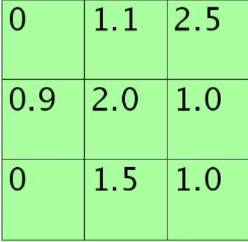
使用stochastic pooling时(即test过程)，其推理过程也很简单，对矩阵区域求加权平均即可。比如对上面的例子求值过程为为：
0*0+1.1*0.11+2.5*0.25+0.9*0.09+2.0*0.2+1.0*0.1+0*0+1.5*0.15+1.0*0.1=1.625 说明此时对小矩形pooling后的结果为1.625.
在反向传播求导时，只需保留前向传播已经记录被选中节点的位置的值，其它值都为0,这和max-pooling的反向传播非常类似。
例子
假设feature map中的pooling区域元素值如下：
3*3大小的，元素值和sum=0+1.1+2.5+0.9+2.0+1.0+0+1.5+1.0=10
方格中的元素同时除以sum后得到的矩阵元素为：
每个元素值表示对应位置处值的概率，现在只需要按照该概率来随机选一个，方法是：将其看作是9个变量的多项式分布，然后对该多项式分布采样即可，theano中有直接的multinomial()来函数完成。当然也可以自己用01均匀分布来采样，将单位长度1按照那9个概率值分成9个区间（概率越大，覆盖的区域越长，每个区间对应一个位置），随机生成一个数后看它落在哪个区间。
比如如果随机采样后的矩阵为：
则这时候的poolng值为1.5
比较
特征提取的误差主要来自两个方面：
（1）邻域大小受限造成的估计值方差增大；
（2）卷积层参数误差造成估计均值的偏移。
mean-pooling能减小第一种误差，更多的保留图像的背景信息，
max-pooling能减小第二种误差，更多的保留纹理信息。
应用
窗口滑动卷积的时候，卷积值就代表了整个窗口的特征。因为滑动的窗口间有大量重叠区域，出来的卷积值有冗余，进行最大pooling或者平均pooling就是减少冗余。
失真不变性，减少冗余的同时，pooling也丢掉了局部位置信息，所以局部有微小形变，结果也是一样的。就像图片上的字母A，局部出现微小变化，也能够被识别成A。而加上椒盐噪音，就是字母A上有很多小洞，同样的能够被识别出来。
平移不变性 如果人们选择图像中的连续范围作为池化区域,并且只是池化相同(重复)的隐藏单元产生的特征,那么,这些池化单元就具有平移不变性 １、连续范围 ２、池化相同隐藏单元产生的特征
而平移不变性，就是一个特征，无论出现在图片的那个位置，都会识别出来。所以平移不变性不是pooling带来的，而是层层的权重共享带来的。
2)
关键点采样(SIFT,SURF关键点都可以)
定点采样，坏处在于不知道采的特征是否具体代表性。
Adaboost等方法特征选择方法选择特征。
下面附上gabor滤波器实现代码
# coding:utf-8import cv2import numpy as npimport pylab as plfrom PIL import Image#构建Gabor滤波器def build_filters():filters = []ksize = [7,9,11,13,15,17] #gabor尺度 6个lamda = np.pi/2.0 # 波长#gabor方向 0 45 90 135for theta in np.arange(0,np.pi,np.pi/4):for k in xrange(6):kern = cv2.getGaborKernel
((ksize[k],ksize[k]),1.0,theta,lamda,0.5,0,
ktype=cv2.CV_32F)
kern /= 1.5*kern.sum()filters.append(kern)return filters#滤波过程def process(img,filters):accum = np.zeros_like(img)for kern in filters:fimg = cv2.filter2D(img,cv2.CV_8UC3,kern)np.maximum(accum,fimg,accum)return accum#特征图生成并显示def getGabor(img,filters):image = Image.open(img)img_ndarray = np.asarray(image)res = [] #滤波结果for i in xrange(len(filters)):res1 = process(img_ndarray,filters[i])res.append(np.asarray(res1))pl.figure(2)for temp in xrange(len(res)):pl.subplot(4,6,temp+1) #画4*6格子pl.imshow(res[temp],cmap='gray')pl.show()return resif __name__ == '__main__':filters = build_filters()getGabor('./test.jpg',filters)
PART
03 结束
往
期
推
荐
1.Tensorflow快速入门
2.Logistic回归实战篇之预测病马死亡率（一）
3.RNN入门与实践
4.史上最详细的XGBoost实战（上）
扫描个人微信号，
拉你进机器学习大牛群。
福利满满，名额已不多…
80%的AI从业者已关注我们微信公众号
