博弈论——完全信息博弈
版权声明:本文为原创文章,未经博主允许不得用于商业用途。
基本概念
一场博弈中的基本属性:
-
N个玩家
-
每个玩家都具有非空备选策略集 A i , i ∈ N A_{i}, i\in N Ai,i∈N
-
收益函数 u i : A 1 × A 2 × . . . × A N → R f o r i ∈ N u_{i}:A_{1}\times A_{2} \times...\times A_{N}\rightarrow R\space for\space i \in N ui:A1×A2×...×AN→R for i∈N (即所有策略的笛卡儿积作为总体策略集合,其中每个玩家的每种策略都对应一个收益)
- 收益函数可以被偏序关系取代
-
博弈结果(outcome): a = ( a 1 , a 2 , . . . , a N ) a=(a_{1},a_{2},...,a_{N}) a=(a1,a2,...,aN),其中 a i a_{i} ai对应第i个玩家所选的策略
-
结果空间(outcome space): A = A 1 × A 2 × . . . × A N A=A_{1}\times A_{2} \times...\times A_{N} A=A1×A2×...×AN
-
对于每种结果,定义 a − i = ( a 1 , . . . a i − 1 , a i + 1 , . . . a N ) = a / a i a_{-i}=(a_{1},...a_{i-1},a{i+1},...a_{N})=a/a_{i} a−i=(a1,...ai−1,ai+1,...aN)=a/ai,即当玩家i选择策略a时其余玩家采取的策略
-
A − i = A 1 × . . . × A i − 1 × A i + 1 × . . . × A N A_{-i}=A_{1}\times ...\times A_{i-1}\times A_{i+1}\times...\times A_{N} A−i=A1×...×Ai−1×Ai+1×...×AN,即其余玩家的结果空间
-
纳什均衡:策略 a a a为纳什均衡点当且仅当:
∀ i ∈ N , ∀ a i ∈ A i , u i ( a i ∗ , a − i ∗ ) ≥ u i ( a i , a − i ∗ ) \forall i\in N, \forall a_{i}\in A_{i},u_{i}(a^{*}_{i}, a^{*}_{-i})\geq u_{i}(a_{i}, a_{-i}^{*}) ∀i∈N,∀ai∈Ai,ui(ai∗,a−i∗)≥ui(ai,a−i∗),即所有玩家的策略改变策略都不会获得更多收益,所有玩家都没有改变策略的动机。
-
完全信息博弈即所有玩家的策略偏序关系公开
策略式博弈(Strategy Games)
策略式博弈即为最简单的博弈,具有有限的玩家、非空策略集和收益函数,可以表示为:
G = { N , { A i } i = 1 N , { u i } i = 1 N } G=\{N,\{A_{i}\}_{i=1}^{N},\{u_{i}\}_{i=1}^{N}\} G={N,{Ai}i=1N,{ui}i=1N}
例如经典的囚徒困境可以表示为:
| confess | don’t confess | |
|---|---|---|
| confess | -6 -6 | 0 -12 |
| don’t confess | -12 0 | 0 0 |
玩家: N = { 1 , 2 } N=\{1,2\} N={1,2}
策略: A 1 = A 2 = { c , d } A_{1}=A_{2}=\{c,d\} A1=A2={c,d}
收益: u 1 ( c , c ) = − 6 , u 1 ( c , d ) = 0... u_{1}(c,c)=-6, u_{1}(c,d)=0 ... u1(c,c)=−6,u1(c,d)=0...
寻找纳什均衡方法:
-
u ∈ Z u\in Z u∈Z:
- 1、对每个玩家,找到对于 A − i A_{-i} A−i中每种策略的的最优收益策略。
- 2、满足所有玩家最优策略的策略即为纳什均衡点。
-
u ∈ R u\in R u∈R
- 1、对每个玩家求出其收益最高的函数(以其策略为自变量,导数为0)
- 2、联立所有玩家的等式,满足所有等式的解集
例题:古诺竞争模型(Cournot Competition)
两家公司需要决定生产量q, G = { { 1 , 2 } , { q 1 , q 2 } , { u 1 , u 2 } } G=\{\{1,2\},\{q_{1},q_{2}\},\{u_{1}, u_{2}\}\} G={{1,2},{q1,q2},{u1,u2}}
其中商品价格为 p ( q 1 + q 2 ) = m a x ( 0 , a − b ( q 1 + q 2 ) ) p(q_{1}+q_{2})=max(0,a-b(q_{1}+q_{2})) p(q1+q2)=max(0,a−b(q1+q2))
成本为线性函数 c i ( q i ) = c q i c_{i}(q_{i})=cq_{i} ci(qi)=cqi
收益为 u i ( q 1 , q 2 ) = ( m a x { 0 , a − b ( q 1 + q 2 ) } − c ) q i u_{i}(q_{1}, q_{2})=(max\{0, a-b(q_{1}+q_{2})\}-c)q_{i} ui(q1,q2)=(max{0,a−b(q1+q2)}−c)qi
其中 a > b , c > 0 , q 1 ≥ 0 , q 2 ≥ 0 a>b, c>0, q_{1}\geq 0, q_{2}\geq 0 a>b,c>0,q1≥0,q2≥0
首先寻找player1的纳什均衡,不妨假设其收益大于0,否则他将停止生产。
则其收益函数为: u 1 = ( a − b ( q 1 + q 2 ) − c ) q 1 u_{1}=(a-b(q_{1}+q_{2})-c)q_{1} u1=(a−b(q1+q2)−c)q1
对 q 1 q_{1} q1求导: u ′ = − 2 b q 1 + a − c − b q 2 u'=-2bq_{1}+a-c-bq_{2} u′=−2bq1+a−c−bq2,导数为0时取得收益最大值,此时 q 1 = a − c − b q 2 2 b q_{1}=\frac{a-c-bq_{2}}{2b} q1=2ba−c−bq2
对于player2根据对称性可得 q 2 = a − c − b q 1 2 b q_{2}=\frac{a-c-bq_{1}}{2b} q2=2ba−c−bq1,
联立两等式解得: q 1 ∗ = q 2 ∗ = a − c 3 b q_{1}^{*}=q_{2}^{*}=\frac{a-c}{3b} q1∗=q2∗=3ba−c,即 a ∗ = ( a − c 3 b , a − c 3 b ) a^{*}=(\frac{a-c}{3b}, \frac{a-c}{3b}) a∗=(3ba−c,3ba−c)
可以拓展到N个玩家博弈,此时同理根据对称性,所有玩家的策略都为 a − c ( n + 1 ) b ) \frac{a-c}{(n+1)b}) (n+1)ba−c)
混合策略博弈(Mixed Strategy)
由于纯策略式博弈经常没有纳什均衡点,因此引入混合策略博弈。
基本概念:
在混合策略中每个玩家的策略集为 Δ ( A i ) \Delta (A_{i}) Δ(Ai)为定义在 R N R^{N} RN上的所有概率分布函数。即为每种策略分配一个概率。
则博弈结果即为 p = ( p 1 , p 2 , . . . p N ) , w h e r e p i ∈ Δ ( A i ) p=(p_{1},p_{2},...p_{N}),\ where\ p_{i}\in \Delta (A_{i}) p=(p1,p2,...pN), where pi∈Δ(Ai),博弈收益函数应为混合策略的收益期望值,即为 U i ( p ) = ∑ a ∈ A p ( a ) u i ( a ) U_{i}(p)=\sum_{a\in A} p(a)u_{i}(a) Ui(p)=∑a∈Ap(a)ui(a)
定理:所有有限博弈都具有混合策略纳什均衡(MNE)
可以证明当所有人的任何纯策略收益相等时可以达到纳什均衡
例题:
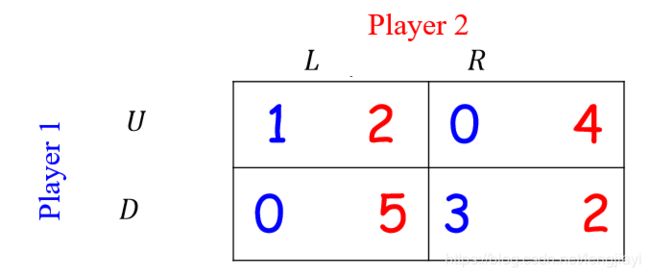
如图所示,Player1的最优策略为(U,L), (D, R),Player2的最优策略的为(U, R), (D, L),因此没有纳什均衡点。
如果使用混合策略,则令 p 1 = ( m , 1 − m ) , p 2 = ( n , 1 − n ) p_{1}=(m,1-m), p_{2}=(n,1-n) p1=(m,1−m),p2=(n,1−n),则:
Player2取L时Player1收益 U 1 = 2 m + 5 ( 1 − m ) U_{1}=2m+5(1-m) U1=2m+5(1−m)
Player2取R时Player1收益 U 1 = 4 m + 2 ( 1 − m ) U_{1}=4m+2(1-m) U1=4m+2(1−m)
联立解得:m=3/5
同理求得:n=3/4
因此混合策略纳什均衡时策略为: p 1 = ( 3 / 5 , 2 / 5 ) , p 2 = ( 3 / 4 , 1 / 4 ) p_{1}=(3/5, 2/5), p_{2}=(3/4, 1/4) p1=(3/5,2/5),p2=(3/4,1/4)
占优策略(Dominant Strategy)
基本概念:
- 弱(weakly)占优策略:如果任意情况下( ∀ a − i ∈ A − i \forall a_{-i}\in A_{-i} ∀a−i∈A−i)玩家某一策略的收益不差于其他任意策略,则此策略弱占优。
- 严格(strictly)占优策略:如果玩家某一策略的收益优于其他任意策略,则此策略严格占优。
显然当一个博弈中某个玩家存在占优策略时,其一定会选择占优策略作为博弈结果。
对应的也有被占优策略:
- 弱被占优策略(Weakly Dominated Strategy):若对于所有情况下玩家的策略a不优于另一策略b,则策略a被b弱占优。
- 严格被占优策略(Strictly DS):若一个策略a差于策略b,则a被b严格占优。
显然如果a被b严格占优则a是永远不会被选择的,因此可以借此缩小博弈的规模。
对于混合策略,如果存在某种混合策略p’收益永远高于p,则p被p’严格占优(易知如果a在纯策略中被严格占优则在混合策略中被严格占优,反之不成立)。
- 信念(Belief):对于一种混合策略博弈博弈的结果 p = ( p i , p − i ) p=(p_{i},p_{-i}) p=(pi,p−i), p − i p_{-i} p−i即为一个信念。简单来说就是玩家i对于其他玩家行为在 Δ A − i \Delta A_{-i} ΔA−i上的一种合理推测。
- 理性(rationality):在某种信念下的最优策略就是理性的。
- 所有在混合策略纳什均衡中概率不为零的纯策略都是理性的,换句话说只要没有被严格占优就是理性策略。
例题1:
第二高价竞拍模型:
有N个玩家参与竞拍,对于每位玩家商品的实际价值为 v i ≥ 0 v_{i}\geq 0 vi≥0,竞拍价格为 b i ≥ 0 b_{i}\geq 0 bi≥0,收益为 v i − b i v_{i}-b_{i} vi−bi
竞拍规则为最高价者成功,并且按照第二高竞拍价格交易。
对于每个玩家, b i = v i b_{i}=v_{i} bi=vi为一个弱占优策略,因此纳什均衡策略为 ( v 1 , v 2 , . . . , v N ) (v_{1},v_{2},...,v_{N}) (v1,v2,...,vN)
证明:
不失一般性的,对于第i个玩家:
-
若存在另一玩家竞价 b k > v i b_{k}>v_{i} bk>vi,则玩家i会停止竞价保证收益>0。
-
若所有玩家的竞价都低于 v i v_{i} vi,则玩家i的收益为 v i − b i v_{i}-b_{i} vi−bi,设其余玩家最高竞价为 b k < v i b_{k}<v_{i} bk<vi,则只需 b i > b k b_{i}>b_{k} bi>bk即可竞拍成功,此时收益为 b k − v i b_{k}-v_{i} bk−vi,和玩家i的竞价无关。因此 b i = v i b_{i}=v_{i} bi=vi为弱占优策略。
例题2:
Beauty Contest(选美竞赛)
有n个玩家从[0,50]中选择一个实数作为自己的评分,越接近所有玩家评分均值2/3收益越大:
U = 50 − ( a i − 2 3 ∑ j a j n ) 2 U=50-(a_{i}-\frac{2}{3}\frac{\sum _{j}a_{j}}{n})^{2} U=50−(ai−32n∑jaj)2
显然对于一种信念 a − i a_{-i} a−i,玩家i的最优策略为使后一项为0,此时收益最大为50。即
a i − 2 3 ∑ j a j n = 0 ⇒ ( 3 − 2 n ) a i ∗ = 2 ∑ j ≠ i a j n ⇒ a i ∗ = 2 ∑ j ≠ i a j 3 n − 2 ≤ 2 ( n − 1 ) 50 3 n − 2 a_{i}-\frac{2}{3}\frac{\sum _{j}a_{j}}{n}=0 \Rightarrow (3-\frac{2}{n})a^*_{i}=\frac{2\sum _{j\neq i}a_{j}}{n}\Rightarrow a_{i}^{*}=\frac{2\sum _{j\neq i}a_{j}}{3n-2}\leq \frac{2(n-1)50}{3n-2} ai−32n∑jaj=0⇒(3−n2)ai∗=n2∑j̸=iaj⇒ai∗=3n−22∑j̸=iaj≤3n−22(n−1)50
因此 a i ∗ ∈ [ 0 , 2 ( n − 1 ) 50 3 n − 2 ] a_{i}^{*}\in [0, \frac{2(n-1)50}{3n-2}] ai∗∈[0,3n−22(n−1)50]
由于所有玩家都是理性的,且知道其他玩家都是理性的,因此在第二轮中重复上述推理,则:
a i ∗ ∈ [ 0 , ( 2 ( n − 1 ) 3 n − 2 ) 2 50 ] a_{i}^{*}\in [0, (\frac{2(n-1)}{3n-2})^{2}50] ai∗∈[0,(3n−22(n−1))250]
重复上述过程,由于系数 2 ( n − 1 ) 3 n − 2 ] < 1 \frac{2(n-1)}{3n-2}]<1 3n−22(n−1)]<1,因此最终 a i ∗ ∈ [ 0 , ε ] , ε → 0 a^*_{i}\in[0,\varepsilon], \varepsilon\rightarrow0 ai∗∈[0,ε],ε→0 ,则取极限后 a i ∗ = 0 a_{i}^{*}=0 ai∗=0,即所有玩家的评分都为0。