WebGIS常见坐标及其转换

GIS的瓦片坐标有很多种，很容易搞混。本文就常见坐标与转换进行讲解。

主要经纬度坐标

其中WGS84属于国际标准，其余两个可以通过其提供的接口进行转换。

坐标	常见采用
WGS84	OpenStreetMap、GoogleEarth等
GCJ-02	高德地图
BD-09	百度地图

关于墨卡托投影（Web Mercator）

首先需要说明，墨卡托投影只是一种空间映射方法，目的是为了在二维的平面上展示三维地球，并非一种坐标系。

墨卡托投影，即正轴等角圆柱投影。由荷兰地图学家墨卡托(G.Mercator)于1569年创立。假想一个与地轴方向一致的圆柱切或割于地球，按等角条件，将经纬网投影到圆柱面上，将圆柱面展为平面后，即可得到墨卡托投影。

关于瓦片切割

对于世界地图，尤其是卫星图来说，数据量是非常大的，动辄TB级别数据，所以这就需要一种流式加载的机制。

3维的地球经过墨卡托投影仪后，转成了一个平铺的地图，通过切割这个大图的方式将地图切割成某个固定值的地图块，这每一块，就对应一个瓦片。

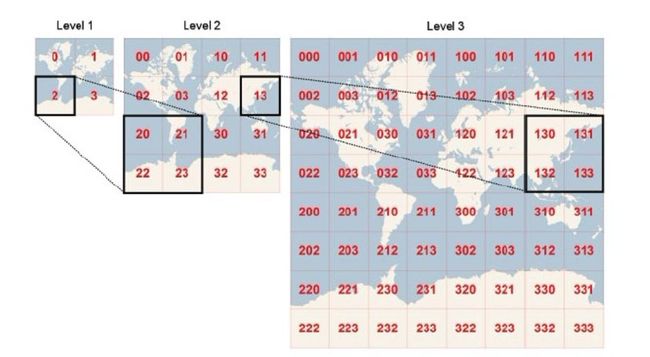
一般情况下，我们见到的都是将地图切割成一个四叉树，即瓦片金字塔。如图所示，金字塔最顶端的为0级，是这个四叉树的根节点，根节点只有一张瓦片，第二层为根节点等分切割的四个更加精细的瓦片。金字塔中的每一片瓦片都可以分割为4个子节点，以此类推，得到这个金字塔。

图：瓦片切割金字塔

**需要注意的是：**Cesium中，0级是一张瓦片，1级是两个瓦片，分别为南北半球，其余级别瓦片都是正常四叉树了。

高德地图的坐标与转换

高德地图的坐标，左方向为X轴，下方向为Y轴，简单理解，就是定义在平面直角坐标系的第四象限。

经纬度坐标转瓦片

（Longitude, Latitude） to （TileX, TileY）

$$TileX=|\frac{longitude+180}{360}\times 2^L|$$

$$TileY=|(\frac{1}{2}-\frac{\ln (\tan \times \frac{\pi }{180})+\sec (latitude\times \frac{\pi }{180})}{2\times \pi }){\times }^L|$$

JavaScript实现

function lnglatToTile(longitude, latitude, level) {
	if (longitude == undefined ||
	    latitude == undefined ||
	    level == undefined) {
        return {longitude, latitude, level}
	}
	let x, y;
    x = Math.abs(((lon + 180) / 360) * Math.pow(2, level));
    y = Math.abs(((1 / 2) - (
    	(Math.log(Math.tan(lat * Math.PI / 180) + 
    	(1 / Math.cos(lat * Math.PI / 180))) / (2 * Math.PI)))) * Math.pow(2, level)
    );
    return {
    	'x': x,
    	'y': y,
    	'z': level
    }
};

经纬度坐标转像素坐标

（Longitude, Latitude） to （PixelX, PixelY）

$$PixelX=|\frac{longitude+180}{360}\times 2^L\times 256\%256|$$

$$pixelY=|(1-\frac{\ln (\tan (latitude\times \frac{\pi }{180})+\frac{1}{\cos (latitude\times \frac{\pi }{180})})}{\pi })\times 2^{Level-1}|$$

瓦片的像素坐标转经纬度坐标

（PixelX, PixelY）to （Longitude, Latitude）

$$Longitude=\frac{TileX+\frac{PixelX}{256}}{2^{Level}}\times 360-180$$

$$Latitude=\arctan (\sinh (\pi -2\times \pi \times \frac{tileY+\frac{pixelY}{256}}{2^{Level}}))\times \frac{180}{\pi }$$

其中L为：Level，当前级别

参考文献：Slippy map tilenames

---

要上班了，待续
更多文章，欢迎戳我的博客
最后编辑于12月6日 13:45 Lichao

微信扫码，在手机上查看：