搞懂卷积神经网络的过拟合、梯度弥散、batchsize的影响的问题
上一篇主要是对卷积神经网络的整个训练过程中公式以及误差的推导给出详细的分析。
博客地址:http://blog.csdn.net/u010402786/article/details/51226825
这一篇主要对卷积神经网络中出现的一些问题进行一个详细的阐述。
第一个问题:模型过拟合
| 1.1 什么是过拟合 |
所谓过拟合(Overfit),是这样一种现象:一个假设在训练数据上能够获得比其他假设更好的拟合,但是在训练数据外的数据集 上却不能很好的拟合数据。此时我们就叫这个假设出现了overfit的现象。

如上图所示:过拟合,就是拟合函数需要顾忌每一个点,最终形成的拟合函数波动很大。在某些很小的区间里,函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值(绝对值)非常大,由于自变量值可大可小,所以只有系数足够大,才能保证导数值很大。
| 1.2 造成过拟合的原因 |
过拟合其中一个可能的成因就是模型的vc维过高,使用了过强的模型复杂度(model complexity)的能力。(参数多并且过训练)
还有一个原因是数据中的噪声,造成了如果完全拟合的话,也许与真实情景的偏差更大。
最后还有一个原因是数据量有限,这使得模型无法真正了解整个数据的真实分布。
权值学习迭代次数足够多(Overtraining),拟合了训练数据中的噪声和训练样例中没有代表性的特征。
| 1.3 过拟合解决方法 |
1.权值衰减
在每次迭代过程中以某个小因子降低每个权值,这等效于修改E的定义,加入一个与网络权值的总量相应的惩罚项,此方法的动机是保持权值较小,避免weight decay,从而使学习过程向着复杂决策面的反方向偏。(L2正则化)
2.适当的stopping criterion(验证集)
3.Cross-validation with some patterns
交叉验证方法 在可获得额外的数据提供验证集合时工作得很好,但是小训练集合的过度拟合问题更为严重
k-fold交叉方法 :
把训练样例分成k份,然后进行k次交叉验证过程,每次使用不同的一份作为验证集合,其余k-1份合并作为训练集合.每个样例会在一次实验中被用作验证样例,在k-1次实验中被用作训练样例;每次实验中,使用上面讨论的交叉验证过程来决定在验证集合上取得最佳性能的迭代次数n*,然后计算这些迭代次数的均值,作为最终需要的迭代次数。
4.正则化
这里有点疑问,正则化是为了防止过拟合还是为了解决过拟合。对部分无用的feature,定义其parameter(p3,p4)非常大,这样会导致训练结果w3,w4非常小,几乎为0,降低模型复杂度。
关于正则化具体的解释请移步到博主另一篇博文中:
( http://blog.csdn.net/u010402786/article/details/49592239 )
第二个问题:数据集不平衡
不平衡训练集会对结果造成很大的负面影响,而训练集在平衡的情况下,能够达到最好的performance。
1. 训练数据分布情况对CNN结果产生很大影响;
2. 平衡的训练集是最优的,数据越不平衡,准确率越差;
3. 如何提升准确率(使用Oversampling)
相关论文是:
《The Impact of Imbalanced Training Data for Convolutional Neural Networks》
第三个问题:Batchsize的影响
| 3.1Batch_Size三种情况 |
Batch_Size(批尺寸)是机器学习中一个重要参数。
①如果数据集比较小,完全可以采用全数据集 ( Full Batch Learning )的形式,这样做至少有 2 个好处:其一,由全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向。其二,由于不同权重的梯度值差别巨大,因此选取一个全局的学习率很困难。
②Batch_Size = 1。这就是在线学习(Online Learning)。使用在线学习,每次修正方向以各自样本的梯度方向修正,横冲直撞各自为政,难以达到收敛。
③如果网络中采用minibatch SGD算法来优化,所以是一个batch一个batch地将数据输入CNN模型中,然后计算这个batch的所有样本的平均损失,即代价函数是所有样本的平均。而batch_size就是一个batch的所包含的样本数,显然batch_size将影响到模型的优化程度和速度。mini batch只是为了充分利用GPU memory而做出的妥协
| 3.2改变Batch_Size的影响 |
在合理范围内,增大 Batch_Size 的好处:内存利用率提高了,大矩阵乘法的并行化效率提高。跑完一次 epoch(全数据集)所需的迭代次数减少,对于相同数据量的处理速度进一步加快。在一定范围内,一般来说 Batch_Size 越大,其确定的下降方向越准,引起训练震荡越小。
下面是参考文献中博主给出的实验结果:
Batch_Size 太小,算法在 200 epoches 内不收敛。
随着 Batch_Size 增大,处理相同数据量的速度越快。
随着 Batch_Size 增大,达到相同精度所需要的 epoch 数量越来越多。
由于上述两种因素的矛盾, Batch_Size 增大到某个时候,达到时间上的最优。
由于最终收敛精度会陷入不同的局部极值,因此 Batch_Size 增大到某些时候,达到最终收敛精度上的最优。
| 3.3 Minibatch简谈 |
首先说一下采用mini-batch时的权重更新规则。比如mini-batch size设为100,则权重更新的规则为:

也就是将100个样本的梯度求均值,替代online learning方法中单个样本的梯度值:

当采用mini-batch时,我们可以将一个batch里的所有样本放在一个矩阵里,利用线性代数库来加速梯度的计算,这是工程实现中的一个优化方法。
一个大的batch,可以充分利用矩阵、线性代数库来进行计算的加速,batch越小,则加速效果可能越不明显。当然batch也不是越大越好,太大了,权重的更新就会不那么频繁,导致优化过程太漫长。
第四个问题:梯度弥散
| 4.1 梯度弥散的解释 |
梯度弥散的问题很大程度上是来源于激活函数的“饱和”。因为在后向传播的过程中仍然需要计算激活函数的导数,所以一旦卷积核的输出落入函数的饱和区,它的梯度将变得非常小。
梯度弥散。使用反向传播算法传播梯度的时候,随着传播深度的增加,梯度的幅度会急剧减小,会导致浅层神经元的权重更新非常缓慢,不能有效学习。这样一来,深层模型也就变成了前几层相对固定,只能改变最后几层的浅层模型。
| 4.2 如何解决梯度弥散 |
一种新的方法batch normalization,相关论文:
《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》
顾名思义,batch normalization嘛,就是“批规范化”咯。Google在ICML文中描述的非常清晰,即在每次SGD时,通过mini-batch来对相应的activation做规范化操作,使得结果(输出信号各个维度)的均值为0,方差为1. 而最后的“scale and shift”操作则是为了让因训练所需而“刻意”加入的BN能够有可能还原最初的输入,从而保证整个network的capacity。

BN可以应用于网络中任意的activation set。文中还特别指出在CNN中,BN应作用在非线性映射前,即对x=Wu+b做规范化。另外对CNN的“权值共享”策略,BN还有其对应的做法(详见文中3.2节)。
那BN到底是什么原理呢?说到底还是为了防止“梯度弥散”。关于梯度弥散,大家都知道一个简单的栗子:。在BN中,是通过将activation规范为均值和方差一致的手段使得原本会减小的activation的scale变大。可以说是一种更有效的local response normalization方法。
参考文献
1.谈谈深度学习中的 Batch_Size
http://blog.csdn.net/ycheng_sjtu/article/details/49804041
2.正则化方法:L1和L2 regularization、数据集扩增、dropout
http://blog.csdn.net/u010402786/article/details/49592239
3.深度学习中 Batch Normalization为什么效果好?
http://www.zhihu.com/question/38102762
训练深度网络的梯度弥散及梯度膨胀问题
在深度网络中,不同层的学习速度差异很大。尤其是在网络后面层学习的情况很好的时候,先前的层常常会在训练时停止不变,基本上学不到东西,这些原因是与基于梯度的学习方法有关。
我们用MNIST数字分类问题作为研究和实验的对象:
这个网络有784个输入神经元,对应于图片28*28=784个像素点,我们设置隐藏神经元为30个,输出层为10个神经元,对应于MNIST的10个数字(0~9),我们训练30epochs,使用minibatch大小为10,学习率为0.01,正则化参数为5.0。在训练时我们也会在验证集上监控分类的准确度。最总我们得到分类准确率为96.48%。
现在另外增加一个隐藏层,同样地是 30 个神经元,试着使用相同的超参数进行训练:
那么就再增加一层同样的隐藏层:
再增加一层:
额外的隐藏层应当让网络能够学到更加复杂的分类函数,然后可以在分类时表现得更好,但实验的结果似乎并不是这样的。 为更加形象的解释这一现象,我们可以将网络学到的东西进行可视化。
下面,画出了一部分[784, 30, 30, 10] 的网络,也就是包含两层各有30 个隐藏神经元的隐藏层。图中的每个神经元有一个条形统计图,表示这个神经元在网络进行学习时改变的速度。更大的条意味着更快的速度,而小的条则表示变化缓慢。更加准确地说,这些条表示了每个神经元上的cost function关于偏置项b的偏导数,也就是代价函数关于神经元的偏差更变的速率delta。因为我们知道delta的数值不仅仅是在学习过程中偏差改变的速度,而且也控制了输入到神经元权重的变量速度。
为了让图里简单,只展示出来最上方隐藏层上的6 个神经元,这里所示的只是中间两个隐藏层,在网络初始化后立即得到训练前期的结果如下:
从上图中我们可以明显的发现这样一个规律,第二个隐藏层上的数值基本上都要比第一个隐藏层上的要大。所以,在第二个隐藏层的神经元将学习得更加快速。为了进一步解释上一结论,使用一种全局的方式来比较学习的速度。我们使用向量delta1和delta2分别表示第一个和第二个隐藏层的学习速率,向量中的每个元素表示该层上每个神经元的小学习速率:
所以,我们可以使用这些向量的长度作为全局衡量这些隐藏层的学习速度的度量。||delta1|| 就代表第一层隐藏层学习速度,而||delta2|| 就代表第二层隐藏层学习速度。
借助这些定义,在和上图同样的配置下,发现||delta1|| = 0.07而||delta2|| =0.31,所以通过数量上的计算也说明了在第二层隐藏层的神经元学习速度确实比第一层要快。
对于三个隐藏层的情况,比如在[784, 30, 30, 30, 10] 的网络中,那么对应的学习速度就是 0.012, 0.060, 0.283。也证明了我们上面的结论。假设我们增加另一个包含30 个隐藏神经元的隐藏层[784, 30, 30, 30, 30, 10] 对应的学习速度是:0.003,0.017, 0.070, 0.285。还是同样说明了前面的层学习速度低于后面的层。
上述的全局速度的计算是刚刚初始化之后的情况。随着训练的推移学习速度变化如下:
对于只有两个隐藏层时net([784, 30, 30, 10]),为了防止使用minibatch随机梯度下降对结果带来更多的噪声,我在 1000 个训练图像上进行了 500 轮 batch 梯度下降,而没有使用minibatch方法。
如图所示,两层在开始时就有着不同的速度。然后两层的学习速度在触底前迅速下落。在最后,我们发现第一层的学习速度变得比第二层更慢了。
对于有四个隐藏层时net([784, 30, 30, 30, 30, 10]),也可以得到与前两种情况相同的结论:前面的隐藏层要比后面的隐藏层学习的更慢。这里,第一层的学习速度和最后一层要差了两个数量级,也就是比第四层慢了100倍,这就比较容易解释为什么在MNIST手写数字识别时,4个隐藏层的网络的效果并没有比2个隐藏层的要好,因为这种速度的下降从另一个角度看实际上是梯度的消失,即使隐藏层多了,但是却并没有学到知识。上述的现象就是我们在深度学习中经常会遇到的梯度弥散问题(vanishing gradient problem)或梯度消失问题
相似的,对于在前面的层中的梯度会变得非常的情况称为爆炸的梯度问题(exploding gradient problem)或梯度膨胀问题。更加一般地说,在深度神经网络中的梯度是不稳定的,在前面的层中或会消失,或会爆炸。这种不稳定性才是深度神经网络中基于梯度学习的根本问题。这就是我们需要理解的东西,如果可能的话,采取合理的步骤措施解决问题。
为了进一步弄清楚为何会出现消失的梯度,来看看一个极简单的深度神经网络:每一层都只有一个单一的神经元。下图就是有三层隐藏层的神经网络:
下面求目标函数C关于第一个神经元的梯度:
先看看下面的sigmoid 函数导数的图像:
也就是说sigmoid函数的导数在0出取得最大值1/4。现在,如果我们使用标准方法来初始化网络中的权重,那么会使用一个均值为0 标准差为 1 的高斯分布。因此所有的权重通常会满足|wj| < 1。所以权重与sigmiod函数导数的乘积是小于1/4的。并且在我们进行了所有这些项的乘积时,最终结果肯定会指数级下降:项越多,乘积的下降的越快。这里我们可以理解了消失的梯度问题的合理解释。
比较目标函数关于第三个神经元和第一个神经元的梯度值,两个表示式有很多相同的项。但是后者还多包含了两个项。由于这些项都是小于1/4的,所以后者的梯度值是前者的 1/16 或者更小。这其实就是消失的梯度出现的本质原因了。
如果乘积项变得很大超过 1,那么我们将不再遇到消失的梯度问题,这时候梯度会在我们 BP 的时候发生指数级地增长。也就是说,我们遇到了梯度爆炸或梯度膨胀的问题,但由于目前我们的初始化策略以及所使用的激活函数的关系,梯度膨胀问题很少出现。
梯度弥散和梯度膨胀都属于不稳定的梯度问题:根本的问题其实是在前面的层上的梯度是来自后面的层上项的乘积。当存在过多的层次时,就出现了内在本质上的不稳定场景。唯一让所有层都接近相同的学习速度的方式是所有这些项的乘积都能得到一种平衡。如果没有某种机制或者更加本质的保证来达成平衡,那网络就很容易不稳定了。简而言之,真实的问题就是神经网络受限于不稳定梯度的问题。所以,如果我们使用标准的基于梯度的学习算法,在网络中的不同层会出现按照不同学习速度学习的情况。
深度学习基础之-梯度弥散和梯度爆炸及解决办法
梯度不稳定问题:深度神经网络中的梯度不稳定性,前面层中的梯度或会消失,或会爆炸。
原因:前面层上的梯度是来自于后面层上梯度的乘乘积。当存在过多的层次时,就出现了内在本质上的不稳定场景,如梯度消失和梯度爆炸。
一、梯度消失问题
为了弄清楚为何会出现消失的梯度,来看看一个极简单的深度神经网络:每一层都只有一个单一的神经元。下图就是有三层隐藏层的神经网络: 


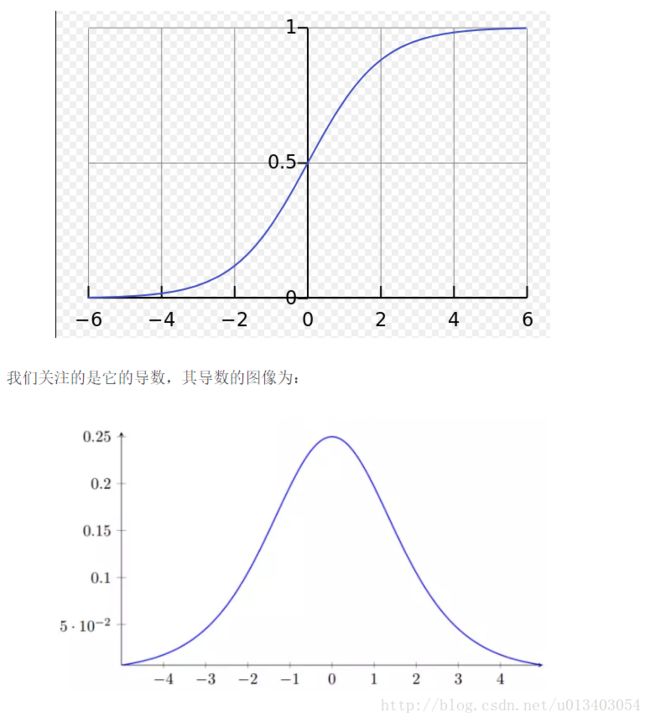
sigmoid函数的导数最大值为1/4。
如果使用一个均值0标准差为1的高斯分布来初始化权值,所有的权重通常会满足 |w|<1。有了这些信息,我们发现会有wjf’(zj)<1/4。并且在我们进行了所有这些项的乘积时,最终结果肯定会指数级下降:项越多,乘积下降的越快。 这,就是梯度消失出现的原因。
二、梯度爆炸
因为sigmoid导数最大为1/4,故当abs(w)>4时我们也有可能得到wjf’(zj)>1的结果,经过多层累乘,梯度会迅速增长,造成梯度爆炸。由此计算出a的数值变化范围很小,仅仅在此窄范围内会出现梯度爆炸问题。而最普遍发生的是梯度消失问题。
三、解决办法
1、激活函数:使用ReLU,maxout激活函数等替代sigmoid。
区别:(1)sigmoid函数值在[0,1],ReLU函数值在[0,+无穷],所以sigmoid函数可以描述概率,ReLU适合用来描述实数;(2)sigmoid函数的梯度随着x的增大或减小消失,而ReLU不会。
ReLU的导数为1,所以f’(zj) = 1。标准的sigmoid输出不具备稀疏性,需要通过惩罚因子来训练一堆接近于0的冗余数据,从而产生稀疏数据,比如L1,L2或者student-t作为惩罚因子,进行regularization。而ReLU为线性修正,是purelin的折线版,作用是如果计算输出小于0,就让它等于0,否则保持原来的值,这是一种简单粗暴地强制某些数据为0的方法,然而经实践证明,训练后的网络完全具备适度的稀疏性,而且训练后的可视化效果和传统pre-training的效果很相似。这说明了ReLU具备引导适度稀疏的能力。
2、BN层
BN(Batch Normalization)层的作用
(1)加速收敛(2)控制过拟合,可以少用或不用Dropout和正则(3)降低网络对初始化权重不敏感(4)允许使用较大的学习率
在每一层输入的时候,加个BN预处理操作。BN应作用在非线性映射前,即对x=Wu+b做规范化。在BN中,是通过将activation规范为均值和方差一致的手段使得原本会减小的activation的scale变大。可以说是一种更有效的local response normalization方法
https://www.lookfor404.com/%E5%85%B3%E4%BA%8E%E6%A2%AF%E5%BA%A6%E6%B6%88%E5%A4%B1%E4%BB%A5%E5%8F%8A%E6%A2%AF%E5%BA%A6%E7%88%86%E7%82%B8/
