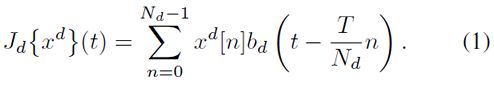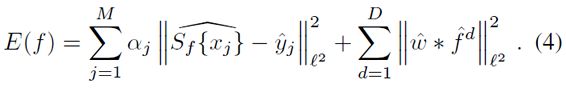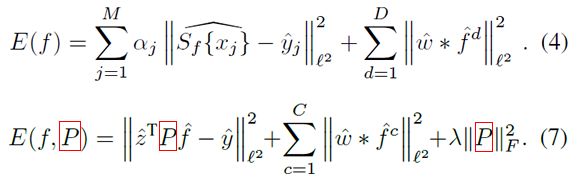目标跟踪之ECO：Efficient Convolution Operators for Tracking

一. 相关滤波算法总结

       作者首先分析了 影响相关滤波算法效率 和 导致过拟合 的几个原因：

1）Model Size (模型大小）

     包括两个方面：

         － 模型层数，对应多分辨率 Sample，比如多层 CNN

         － 特征维度，对应庞大的 HOG or CNN特征图

      这里的效率影响是显而易见的，层数或特征越多，表现力越丰富，计算量也相应的线性增加（如C-COT需要在线学习800,000个参数）。

      另外，也是作者一直Focus的问题，复杂模型带来的Over-Fitting问题，导致准确度下降。

2）Training Set Size（训练集大小）

      训练集 是指所用到的训练数据，只用到上一帧的数据进行计算，效率就比较高；如果要用到之前若干帧的数据进行训练（比如加权平均），效率就会低。

      保留训练集的优点在于，仅仅通过 online learning 会导致新学到的特征出错（比如遮挡），不足以表达正确的对象。

      PS：DSST 仅用上一帧Sample训练，但是是通过和之前模型累加，保留了前面若干帧的信息，在兼顾 训练集 的基础上确保了效率。

3）Model Update（模型更新）

      理想情况下，我们希望每一帧都进行模型更新，实时特征更新能够保证准确性，但同样会带来效率负担，探讨间隔帧模式下的模型更新策略是提高效率的一个思路。

       

二. ECO 方法引入

       针对相关滤波算法存在的上述问题，作者提出了 ECO 方法。

       论文下载：Efficient Convolution Operators for Tracking

       作者提出来三个 Contribution，对应上面三个问题的改进：

1）对卷积操作进行因式分解，减少模型参数

     Factorized convolution operator，通过提取特征子集来 进行降维。

2）简化了训练集生成，并保证Sample多样性

     提出 Generative Sample Space Model，将类似的 Sample 归并到一个 Component，训练样本从多个 Component 中选择。

3）改进模型更新策略

     采用新的 Model Update Strategy，将更新间隔（Ns）设为6，通过测试发现，稀疏更新策略能避免 模型漂移问题（Model Drift），提高速度和健壮性。

三. 算法概要

       针对上面三个方向进行展开，详细描述算法思路。

    > 3.1 Factorized convolution operator

        这篇文章最大的亮点 - 从论文命名也能看得出来，占据了最大的篇幅。

        算法基于C-COT，因此先亮出 C-COT 最关键的公式：

Point 1：提取连续特征

通过 t 进行插值，将特征图（Feature Map）转换到连续的空间域。得到的结果 J{x} 即为提取的特征。

        

Point 2：根据对应层相关滤波器 Filter （f）计算 Score

        

Point 3：定义目标函数

     针对训练样本 xj 构造高斯函数 yj，通过 L2 Norm 构造最小二乘目标函数，并添加权值惩罚项 w，这都是比较常用的做法：

      

     通过 Parseval’s formula 进行傅里叶变换，得到：

        

Point 4：减少滤波器 （new）

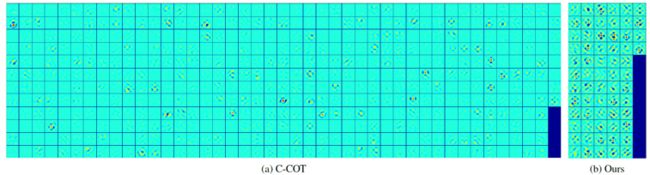
     通过可视化发现，C-COT很多滤波器能量很小，对于结果其实是没什么贡献，因此提出方法 从 D个滤波器中选择贡献最大的C个，进行降维：

        

      作者利用了卷积的线性特征，通过一个 D*C 的系数矩阵 P，将原来的 Score 函数进行如下变换：

       

      同样在原来的目标函数（公式4）基础上得到 新的目标函数（公式7）：

        

       其中 z = J{x}，代入求共轭即得到公式（7），最后加入参数矩阵P的惩罚项，对应权值参数 λ。 

Point 5：目标函数求解（new）

      与原始的Loss函数不同，新定义的Loss公式(7) 是个非线性的最小二乘问题，双线性子项  使得该问题类似矩阵的因式分解问题。

作者采用了 高斯牛顿法（Gauss-Newton）和 共轭梯度法（Conjugate Gradient）来求解。

      求解目标就是 根据输入的训练数据（或者叫训练特征） 得到使得 E最小的 滤波器 f，具体求解过程不再展开了。

    > 3.2 Generative Sample Space Model

        通过对 Sample 分类简化训练集，通过 高斯混合模型（GMM）将样本进行分类，得到不同的 Component：

        

       来看对比：

a）图中上半部分是按照 GMM 得到的 Component 模型，不同 Component 之间差异比较大，采用这种策略选择样本能保证多样性；

b）下半部分是得到的连续帧的训练样本，相邻帧之间的样本近似度很高。

       根据 输入x 和输出 y 的联合概率分布 P(x,y)，将原来的目标函数（论文公式3） 替换成下图下面部分（论文公式10）：

                

       进一步 将原来的 M个样本，替换为 L个（文中L=M/8） Component 的均值 μ，整理得到 公式（12）。

       关于 Component 的建立和替换策略也比较简单，假设我们 Total 要维护 L个Component，那么针对一个新的样本：

1）建立一个 New Component，总的 Component 数量+1；

2）如果 Component 数量超过 L 个，执行下面策略：

      a）将权值最低的 Component 进行替换；

      b）合并权值最低的两个 Component，合并方法如下：

        

       即 权值相加，均值加权求和。

    > 3.3 Model Update Strategy

        模型更新 没什么好说的，间隔帧更新也是工程中经常会用到的方法，这里要提的一点是，关于更新频率取决于视频中待跟踪目标的运动速度，如果目标运动较慢，可以考虑采用间隔较大的方法处理，反之，速度较快的情况下（比如车辆）是不同的。

        

四. 实验效果

       来看和主流方法的对比（VOT2016 数据集），先来看几户是完爆 Top10 的 EAO 曲线：

        

       再来看多个 衡量参数上的对比情况（几乎完胜）：

        

        EAO（Expected average overlap）：跟踪框准确率第一，优化的特征降维 和 多样性样本 起了重要作用；

        健壮性 - Fail（Fail rate）：失败率也很低；

        精确度 - Acc（Accuracy）：精度第二名，仅次于 SSAT；

        速度 - EFO：手动特征选择的 ECO-HC（Hand-Crafted）效率最高，采用 HOG+Color Names，在 i7 CPU上可以跑到 60FPS，

                            采用CNN特征效率一般，在 GPU 上能跑到 8 FPS，也算不错了；