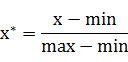kaggle 入门系列翻译（一） minst手写数据集

最近在学习kaggle相关，顺便翻译一下kaggle比赛中大牛的kernel吧，同时加强自己的理解，但愿能坚持下去吧。。

第一次就以minst 数字认真比赛开始吧：

精力有限，每一场比赛只能翻译打星最多的kernel：

本次的链接如下：

https://www.kaggle.com/yassineghouzam/introduction-to-cnn-keras-0-997-top-6

目录：

1、介绍

2、数据预处理

加载数据

检查缺失项

归一化和标准化

重组

标签one-hoting编码

拆分测试和训练集

3、CNN卷积神经网络

定义模型

设置最优化方式和退火算法

数据增强

4、模型评估

训练和评估曲线

混淆矩阵

5、预测和提交

 

 

下面详细介绍：

1、介绍

就是28*28的数据集，通过灰度的不同，来判断这个矩阵代表数字几，0~9

本文主要通过CNN深度学习的方式进行预测。

可以看出，这个主要参考了LeNet的结构。

首先加载所有需要用到的类库：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import seaborn as sns
%matplotlib inline    //ipython特有的，python下会报错，用来开启画图模式

np.random.seed(2)

from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
import itertools

from keras.utils.np_utils import to_categorical # convert to one-hot-encoding
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten, Conv2D, MaxPool2D
from keras.optimizers import RMSprop
from keras.preprocessing.image import ImageDataGenerator
from keras.callbacks import ReduceLROnPlateau


sns.set(style='white', context='notebook', palette='deep')

2、数据预处理

加载数据

train = pd.read_csv("../input/train.csv")
test = pd.read_csv("../input/test.csv")

这边看过七月在线的教程，说这里有个鄙视链，一般参加比赛的，都会把训练集和测试机放在input文件夹下。。。

加载完之后可以看一下数据的样本分布如何：

Y_train = train["label"]

# Drop 'label' column
X_train = train.drop(labels = ["label"],axis = 1) 

# free some space
del train 

g = sns.countplot(Y_train)

Y_train.value_counts()

得到如图结果：

1    4684
7    4401
3    4351
9    4188
2    4177
6    4137
0    4132
4    4072
8    4063
5    3795
Name: label, dtype: int64

可以看出，分布还是比较均衡的。

检查缺失项

X_train.isnull().any().describe()

test.isnull().any().describe()

 

结果发现很完整，无需处理了就

 

归一化和标准化

这里做了归一化，说可以减少照明的影响。

normlization 归一化

standardization 标准化

这里就是使用的归一化：

标准化石如下公式：

1、在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，第二种方法(Z-score standardization)表现更好。

2、在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用第一种方法或其他归一化方法。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。

X_train = X_train / 255.0
test = test / 255.0

重组

原有数据是784维度的，后面处理时希望把他变成图像那样的矩阵式，变成28*28的

X_train = X_train.values.reshape(-1,28,28,1)
test = test.values.reshape(-1,28,28,1)

这里因为是灰度图，所以最后一项只有1，如果是rbg这种，就得变成3了。

参数-1代表新数组的shape属性应该要与原来数组的一致，即新数组元素数量与原数组元素数量要相等。

标签one-hoting编码

最终分类的是10个类别，进行one-hot encoding：

Y_train = to_categorical(Y_train, num_classes = 10)

拆分测试和训练集

 

random_seed = 2

X_train, X_val, Y_train, Y_val = train_test_split(X_train, Y_train, test_size = 0.1, random_state=random_seed)

random_seed 随机数种子，貌似设不设置无所谓，只是让每次拆分的结果固定。

这里由于测试机是比较均衡的，所以这么分没问题，如果不均衡的话这么分就不行了，文章中说通过stratify = True可以解决。

正常应该可以通过下采样；或者将多的那部分样本拆分，拆分后的集合和少的那部分训练，而后将多个训练结果融合；

g = plt.imshow(X_train[0][:,:,0])

通过这个方式看一下当前样本的形态。

 

3、CNN卷积神经网络

定义模型

这里使用keras框架实现cnn，keras底层选择的tensorflow。

其中主要用到了以下几种层：

卷积层：(conv)使用多个表决器来扫描同一副图像得到不同的结果，同一个核w权重不变，不断扫描一幅图片，得到一个新的图片。

池化层：主要用于减少参数维数，防止过拟合。同时可以让数据具有一些不变性。

dropout:(不知道中文怎么翻译)防止过拟合，随机设置网络中部分节点权重为0.原理大概如下：有几次网络中，有节点a的权重不为0的情况下，分类结果是A,但是还有很多a权重为0的情况下，他依然分类结果A，可认为a对真实的分类其实意义不是特别大。

激活层（这里用了relu，但两者是一对多的关系）这层有时介绍网络时会包括在卷积层，是必须有的，可以预见，如果没有这一层的话，连续两个卷积层连在一起，可以w1(w2*x)可以理解为w*x，失去了意义。所以需要激活层。

扁平层：(Flatten layer) 全连接之前的过度层，多维转化为一维

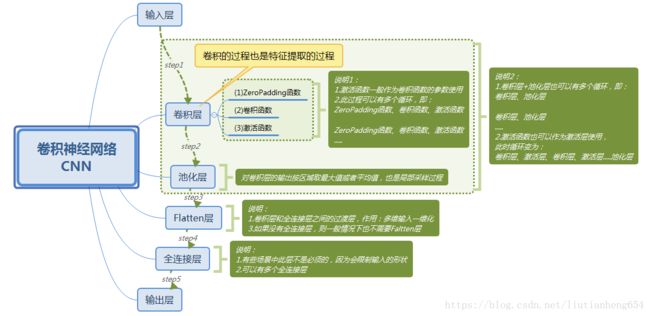
网上有个图，画的比较好：

模型内容：首先是2个32核的卷积层，然后一个最大值池化层，然后一个dropout,然后两个64核的卷积层。之后池化，dropout，而后一个扁平层之后上激活函数，而后再一个dropout之后上激活函数。

# Set the CNN model 
# my CNN architechture is In -> [[Conv2D->relu]*2 -> MaxPool2D -> Dropout]*2 -> Flatten -> Dense -> Dropout -> Out

model = Sequential()

model.add(Conv2D(filters = 32, kernel_size = (5,5),padding = 'Same', 
                 activation ='relu', input_shape = (28,28,1)))
model.add(Conv2D(filters = 32, kernel_size = (5,5),padding = 'Same', 
                 activation ='relu'))
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Dropout(0.25))


model.add(Conv2D(filters = 64, kernel_size = (3,3),padding = 'Same', 
                 activation ='relu'))
model.add(Conv2D(filters = 64, kernel_size = (3,3),padding = 'Same', 
                 activation ='relu'))
model.add(MaxPool2D(pool_size=(2,2), strides=(2,2)))
model.add(Dropout(0.25))


model.add(Flatten())
model.add(Dense(256, activation = "relu"))
model.add(Dropout(0.5))
model.add(Dense(10, activation = "softmax"))

设置最优化方式和退火算法

 

为了让收敛加快，并尽量防止最终在最小值处不断摇摆，采用一个不断减小的步长。

（并尽量防止进入局部最小值，采用了模拟退火算法，这段还未理解到底有没有用）。

这里插一个模拟退火算法的理解：

模仿兵器淬火的过程，多次放在水里降温的过程。

相当于右半个余弦的样子，不断重复：就是步长慢慢减小到0后又一下子增加一节，然后再慢慢减少。

当连续三次结果没有优化的话，将训练步长减半。

optimizer = RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0)
model.compile(optimizer = optimizer , loss = "categorical_crossentropy", metrics=["accuracy"])
learning_rate_reduction = ReduceLROnPlateau(monitor='val_acc', 
                                            patience=3, 
                                            verbose=1, 
                                            factor=0.5, 
                                            min_lr=0.00001)

epochs = 1 # Turn epochs to 30 to get 0.9967 accuracy
batch_size = 86

数据增强

为防止过拟合，我们可以通过对原有数据集的变换组合，生成新的数据集，从而让训练得到的模型更加鲁棒。

比如平移，缩放，旋转。

这里采用了四种方式：

旋转10度之内

缩放10%之内

水平移动10%以内

垂直移动10%以内

经过这个变换后产生的数据集，最终严重结果得到了1%的提升。

datagen = ImageDataGenerator(
        featurewise_center=False,  # set input mean to 0 over the dataset
        samplewise_center=False,  # set each sample mean to 0
        featurewise_std_normalization=False,  # divide inputs by std of the dataset
        samplewise_std_normalization=False,  # divide each input by its std
        zca_whitening=False,  # apply ZCA whitening
        rotation_range=10,  # randomly rotate images in the range (degrees, 0 to 180)
        zoom_range = 0.1, # Randomly zoom image 
        width_shift_range=0.1,  # randomly shift images horizontally (fraction of total width)
        height_shift_range=0.1,  # randomly shift images vertically (fraction of total height)
        horizontal_flip=False,  # randomly flip images
        vertical_flip=False)  # randomly flip images


datagen.fit(X_train)

# Fit the model
history = model.fit_generator(datagen.flow(X_train,Y_train, batch_size=batch_size),
                              epochs = epochs, validation_data = (X_val,Y_val),
                              verbose = 2, steps_per_epoch=X_train.shape[0] // batch_size
                              , callbacks=[learning_rate_reduction])

通过学习曲线看看能否收敛，看看算法效果如何。

4、模型评估

训练和评估曲线

# Plot the loss and accuracy curves for training and validation 
fig, ax = plt.subplots(2,1)
ax[0].plot(history.history['loss'], color='b', label="Training loss")
ax[0].plot(history.history['val_loss'], color='r', label="validation loss",axes =ax[0])
legend = ax[0].legend(loc='best', shadow=True)

ax[1].plot(history.history['acc'], color='b', label="Training accuracy")
ax[1].plot(history.history['val_acc'], color='r',label="Validation accuracy")
legend = ax[1].legend(loc='best', shadow=True)

 

混淆矩阵

通过混淆矩阵来看看模型的性能，看看还有没有什么能改进的：

# Look at confusion matrix 

def plot_confusion_matrix(cm, classes,
                          normalize=False,
                          title='Confusion matrix',
                          cmap=plt.cm.Blues):
    """
    This function prints and plots the confusion matrix.
    Normalization can be applied by setting `normalize=True`.
    """
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=45)
    plt.yticks(tick_marks, classes)

    if normalize:
        cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]

    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, cm[i, j],
                 horizontalalignment="center",
                 color="white" if cm[i, j] > thresh else "black")

    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')

# Predict the values from the validation dataset
Y_pred = model.predict(X_val)
# Convert predictions classes to one hot vectors 
Y_pred_classes = np.argmax(Y_pred,axis = 1) 
# Convert validation observations to one hot vectors
Y_true = np.argmax(Y_val,axis = 1) 
# compute the confusion matrix
confusion_mtx = confusion_matrix(Y_true, Y_pred_classes) 
# plot the confusion matrix
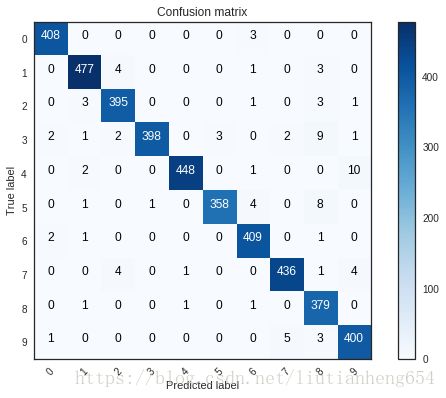
plot_confusion_matrix(confusion_mtx, classes = range(10)) 

可以看出相对42000的数据量，结果已经很好了，只有4有些会被五分类为9，我们可以看一下为什么。

# Display some error results 

# Errors are difference between predicted labels and true labels
errors = (Y_pred_classes - Y_true != 0)

Y_pred_classes_errors = Y_pred_classes[errors]
Y_pred_errors = Y_pred[errors]
Y_true_errors = Y_true[errors]
X_val_errors = X_val[errors]

def display_errors(errors_index,img_errors,pred_errors, obs_errors):
    """ This function shows 6 images with their predicted and real labels"""
    n = 0
    nrows = 2
    ncols = 3
    fig, ax = plt.subplots(nrows,ncols,sharex=True,sharey=True)
    for row in range(nrows):
        for col in range(ncols):
            error = errors_index[n]
            ax[row,col].imshow((img_errors[error]).reshape((28,28)))
            ax[row,col].set_title("Predicted label :{}\nTrue label :{}".format(pred_errors[error],obs_errors[error]))
            n += 1

# Probabilities of the wrong predicted numbers
Y_pred_errors_prob = np.max(Y_pred_errors,axis = 1)

# Predicted probabilities of the true values in the error set
true_prob_errors = np.diagonal(np.take(Y_pred_errors, Y_true_errors, axis=1))

# Difference between the probability of the predicted label and the true label
delta_pred_true_errors = Y_pred_errors_prob - true_prob_errors

# Sorted list of the delta prob errors
sorted_dela_errors = np.argsort(delta_pred_true_errors)

# Top 6 errors 
most_important_errors = sorted_dela_errors[-6:]

# Show the top 6 errors
display_errors(most_important_errors, X_val_errors, Y_pred_classes_errors, Y_true_errors)

可以看出来，这个人都没办法分。。写的太丑了。所以忽略不计了。

5、预测和提交

后面就是预测并提交了

# predict results
results = model.predict(test)

# select the indix with the maximum probability
results = np.argmax(results,axis = 1)

results = pd.Series(results,name="Label")
submission = pd.concat([pd.Series(range(1,28001),name = "ImageId"),results],axis = 1)

submission.to_csv("cnn_mnist_datagen.csv",index=False)

第一次就到这了，后面会把这一篇慢慢完善，下一篇房价那个或者泰坦尼克号的吧。。欢迎交流啊，邮箱：[email protected]