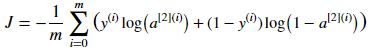吴恩达深度学习第三周作业（Planar data classification with one hidden layer)

本次实现具有一个隐藏层的神经网络

1.导入需要使用的库

import numpy as np
from testCases import *
import matplotlib.pyplot as plt
import pylab
import sklearn
import sklearn.datasets
import sklearn.linear_model

2.我们使用一个函数load_planar_dataset()加载数据集，该函数如下：

def load_planar_dataset():
    np.random.seed(1)
    m = 400  # 样本数量
    N = int(m / 2)  # 每个类别的样本量
    D = 2  # 维度数
    X = np.zeros((m, D))  # 初始化X
    Y = np.zeros((m, 1), dtype='uint8')  # 初始化Y
    a = 4  # 花儿的最大长度

    for j in range(2):
        ix = range(N * j, N * (j + 1))
        t = np.linspace(j * 3.12, (j + 1) * 3.12, N) + np.random.randn(N) * 0.2  # theta
        r = a * np.sin(4 * t) + np.random.randn(N) * 0.2  # radius
        X[ix] = np.c_[r * np.sin(t), r * np.cos(t)]
        Y[ix] = j

    X = X.T
    Y = Y.T

    return X, Y

调用该函数，可以将图像显示出来：

我在写到此处时，出现了一个bug，按照网上写的是c=Y，发现存在维度不同的问题，此处X[0 , :]维度是（400,), Y维度为(1,400),

报错为：c of shape (1, 400) not acceptable as a color sequence for x with size 400, y with size 400

然后我利用Y.reshape(X[0,:].shape),把c的维度也变成了（400，）,虽然老师说我们要尽量少使用（400,），这种秩为1的数组，但是我此处把c 使用reshape为(400,)

X,Y=load_planar_dataset()
plt.scatter(X[0, :], X[1, :],c=Y.reshape(X[0,:].shape),  s=40, cmap=plt.cm.Spectral);
plt.show()

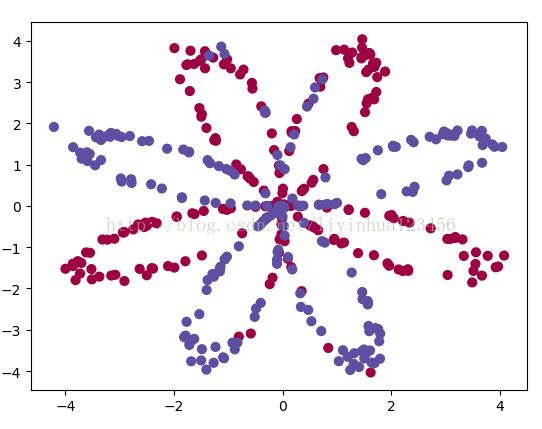
对于y=0时，显示为红色的点；而当y=1时，显示的是蓝色的点。

我们的目标是把这两种颜色点分开

查看训练集的维度

shape_X=X.shape
shape_Y=Y.shape
m=X.shape[1]
print("the shape of X is:"+str(shape_X))
print("the shape of Y is:"+str(shape_Y))
print("the training examples:" +str(m))

首先我们调用sklearn的内置函数来实现简单的逻辑回归来对这些点进行二分类

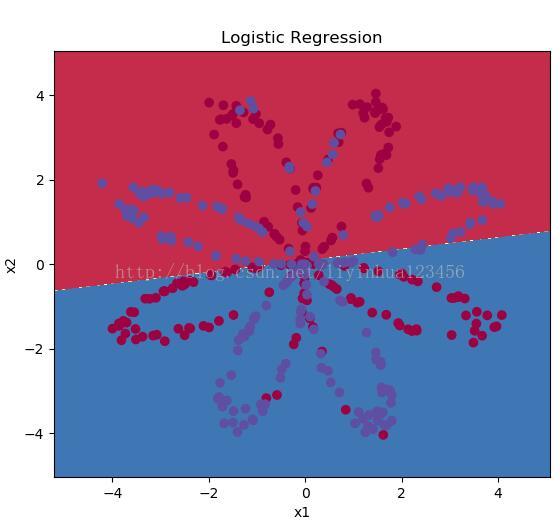
clf = sklearn.linear_model.LogisticRegressionCV();
clf.fit(X.T, Y.T);
plot_decision_boundary(lambda x: clf.predict(x), X, Y)
plt.title("Logistic Regression")
# Print accuracy
LR_predictions = clf.predict(X.T)
print ('Accuracy of logistic regression: %d ' % float(
    (np.dot(Y, LR_predictions) + np.dot(1 - Y, 1 - LR_predictions)) / float(Y.size) * 100) +
       '% ' + "(percentage of correctly labelled datapoints)")
 #Accuracy of logistic regression: 47 % (percentage of correctly labelled datapoints)

其中plot_decision_boundary的实现如下：

def plot_decision_boundary(model, X, y):
    # Set min and max values and give it some padding
    x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
    y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole grid
    Z = model(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.ylabel('x2')
    plt.xlabel('x1')
    plt.scatter(X[0, :], X[1, :], c=y.reshape(X[0,:].shape), cmap=plt.cm.Spectral)

得到的分割图像为：

但是我们发现使用logistic regression进行分类只达到了47%的正确率

接下来我们使用含有一个神经网络的模型，来实现该分类

首先介绍关于建立一个神经网络通用过程

# Step1：设计网络结构，例如多少层，每层有多少神经元等。
#
# Step2：初始化模型的参数
#
# Step3：循环
#
#     Step3.1：前向传播计算
#
#     Step3.2：计算代价函数
#
#     Step3.3：反向传播计算
#
#     Step3.4：更新参数

接下来，我们就逐个实现这个过程中需要用到的相关函数，并整合至nn_model()中。

当nn_model()模型建立好后，我们就可以用于预测或新数据集的训练与使用。

定义网络结构

# 初始化输入层n_x，隐含层n_h，输出层的层数n_y
def layer_size(X,Y):
    """
        Arguments:
        X -- input dataset of shape (input size, number of examples)
        Y -- labels of shape (output size, number of examples)

        Returns:
        n_x -- the size of the input layer
        n_h -- the size of the hidden layer
        n_y -- the size of the output layer
    """
    n_x=X.shape[0]
    n_h=4
    n_y=Y.shape[0]
    return (n_x,n_h,n_y)

初始化参数W,b

W初始化为很小的数，b初始化为0

def initialize_parameters(n_x,n_h,n_y):
    """
       Argument:
       n_x -- size of the input layer
       n_h -- size of the hidden layer
       n_y -- size of the output layer

       Returns:
       params -- python dictionary containing your parameters:
                       W1 -- weight matrix of shape (n_h, n_x)
                       b1 -- bias vector of shape (n_h, 1)
                       W2 -- weight matrix of shape (n_y, n_h)
                       b2 -- bias vector of shape (n_y, 1)
       """
    np.random.seed(2)
    W1=np.random.randn(n_h,n_x)*0.01
    b1 = np.zeros((n_h, 1)) * 0.01
    W2=np.random.randn(n_y,n_h)*0.01
    b2=np.zeros((n_y,1))
    assert(W1.shape==(n_h,n_x))
    assert(b1.shape==(n_h,1))
    assert(W2.shape==(n_y,n_h))
    assert(b2.shape==(n_y,1))
    parameters={"W1":W1,"b1":b1,"W2":W2,"b2":b2}
    return parameters

接下来进行循环

首先是前向传播

def foward_propagation(X,parameters):
    """
        Argument:
        X -- input data of size (n_x, m)
        parameters -- python dictionary containing your parameters (output of initialization function)

        Returns:
        A2 -- The sigmoid output of the second activation
        cache -- a dictionary containing "Z1", "A1", "Z2" and "A2"
        """
    W1=parameters["W1"]
    b1=parameters["b1"]
    W2=parameters["W2"]
    b2=parameters["b2"]
    Z1=np.dot(W1,X)+b1
    A1=np.tanh(Z1)
    Z2=np.dot(W2,A1)+b2
    A2=1/(1+np.exp(-Z2))
    assert(A2.shape==(1,X.shape[1]))
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    return A2,cache

接下来计算损失函数：

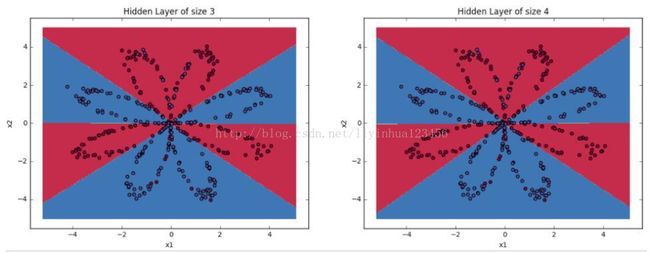
def compute_cost(A2,Y,parameters):
    """
       Computes the cross-entropy cost given in equation (13)

       Arguments:
       A2 -- The sigmoid output of the second activation, of shape (1, number of examples)
       Y -- "true" labels vector of shape (1, number of examples)
       parameters -- python dictionary containing your parameters W1, b1, W2 and b2

       Returns:
       cost -- cross-entropy cost given equation (13)
       """
    m=Y.shape[1]
    logprobs=np.multiply(np.log(A2),Y)+np.multiply(np.log(1-A2),1-Y)
    cost=-np.sum(logprobs)/m
    cost=np.squeeze(cost)
    assert (isinstance(cost, float))
    return cost

然后，我们需要利用之前的cache来进行反向传播计算，计算公式如下：

def backward_propagation(parameters,cache,X,Y):
    """
        Implement the backward propagation using the instructions above.

        Arguments:
        parameters -- python dictionary containing our parameters
        cache -- a dictionary containing "Z1", "A1", "Z2" and "A2".
        X -- input data of shape (2, number of examples)
        Y -- "true" labels vector of shape (1, number of examples)

        Returns:
        grads -- python dictionary containing your gradients with respect to different parameters
        """
    m=X.shape[1]
    W1=parameters["W1"]
    W2=parameters["W2"]
    A1 = cache["A1"]
    A2 = cache["A2"]
    dZ2 = A2 - Y
    dW2 = np.dot(dZ2, A1.T) / m
    db2 = np.sum(dZ2, axis=1, keepdims=True) / m
    dZ1 = np.multiply(np.dot(W2.T, dZ2), (1 - np.power(A1, 2)))
    dW1 = np.dot(dZ1, X.T) / m
    db1 = np.sum(dZ1, axis=1, keepdims=True) / m

    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}
    return grads

接下来我们使用dW，db来更新w，b

def update_parameter(parameters,grads,learning_rate=1.2):
    """
        Updates parameters using the gradient descent update rule given above

        Arguments:
        parameters -- python dictionary containing your parameters
        grads -- python dictionary containing your gradients

        Returns:
        parameters -- python dictionary containing your updated parameters
        """
    # Retrieve each parameter from the dictionary "parameters"
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]

    # Retrieve each gradient from the dictionary "grads"
    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]

    # Update rule for each parameter
    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2

    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}

    return parameters

整合到nn_model(）函数中

def nn_model(X,Y,n_h,num_iterations=10000,print_cost=False):
    """
       Arguments:
       X -- dataset of shape (2, number of examples)
       Y -- labels of shape (1, number of examples)
       n_h -- size of the hidden layer
       num_iterations -- Number of iterations in gradient descent loop
       print_cost -- if True, print the cost every 1000 iterations

       Returns:
       parameters -- parameters learnt by the model. They can then be used to predict.
       """
    # np.random.seed(3)
    n_x=layer_size(X,Y)[0]
    n_y=layer_size(X,Y)[2]
    parameters=inititalize_parameters(n_x,n_h,n_y)
    W1=parameters["W1"]
    b1=parameters["b1"]
    W2=parameters["W2"]
    b2=parameters["b2"]
    for i in range(0,num_iterations):
        A2,cache=foward_propagation(X,parameters)
        cost=compute_cost(A2,Y,parameters)
        grads=backward_propagation(parameters,cache,X,Y)
        parameters=update_parameter(parameters,grads)
        if print_cost and i%1000==0:
            print("cost after iteratin %i:%f"%(i,cost))
    return parameters

上面是训练一个单隐藏层神经网络的过程，下面要使用它进行预测

def predict(parameters,X):
    """
        Using the learned parameters, predicts a class for each example in X

        Arguments:
        parameters -- python dictionary containing your parameters 
        X -- input data of size (n_x, m)

        Returns
        predictions -- vector of predictions of our model (red: 0 / blue: 1)
        """
    A2,cache=foward_propagation(X, parameters)
    prediction=(A2 > 0.5)
    return prediction

到目前为止，我们已经实现了完整的神经网络模型和预测函数，接下来，我们用我们的数据集来训练一下：

parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)
# Plot the decision boundary
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
pylab.show()
predictions=predict(parameters,X)
print ('Accuracy: %d' % float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100) + '%')

相比47%的逻辑回归预测率，使用含有一个隐藏层的神经网络预测的准确度可以达到90%。

接下来我们可以调整隐藏层神经元的数目来观察结果

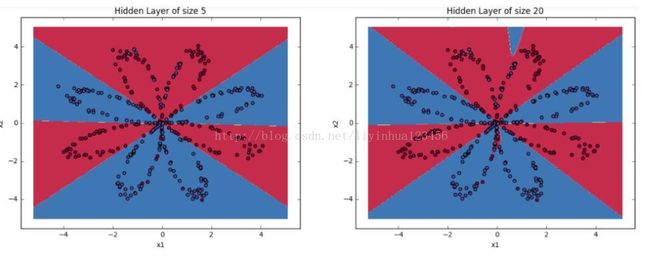
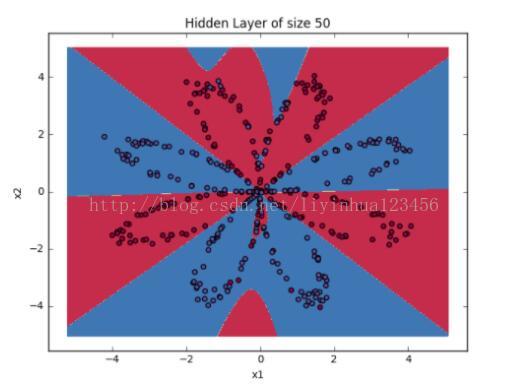
#调整隐藏层神经元的数目观察结果
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]
for i, n_h in enumerate(hidden_layer_sizes):
    plt.subplot(5, 2, i+1)
    plt.title('Hidden Layer of size %d' % n_h)
    parameters = nn_model(X, Y, n_h, num_iterations = 5000)
    plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)

    predictions = predict(parameters, X)
    accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)
    print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))
    pylab.show()

Accuracy for 1 hidden units: 67.5 %
Accuracy for 2 hidden units: 67.25 %
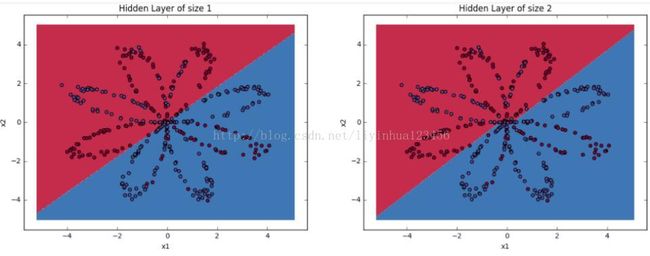
Accuracy for 3 hidden units: 90.75 %
Accuracy for 4 hidden units: 90.5 %
Accuracy for 5 hidden units: 91.25 %
Accuracy for 20 hidden units: 90.0 %
Accuracy for 50 hidden units: 90.25 %

对比结果，我们发现：

1.神经元数目越多，生成的分割曲线越复杂，最终越可能导致过拟合。

2.对该应用而言，最好的神经元数目是n_h=5，此时，几乎没有过拟合问题发生。