无人机飞控姿态解析

博主：UAV

声明：尊重版权，转载请注明出处。

原文地址：

联系方式：595493514@qq.com

技术交流QQ：595493514

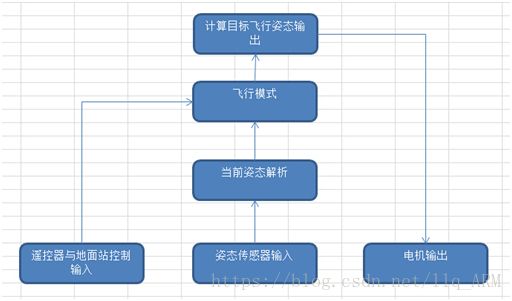
其中飞行控制原理如图1：

1.  通过加速度计，陀螺仪，磁罗盘，GPS等姿态传感器采集当前无人姿态，并进行姿态解析。

2.  通过地面站或者遥控器设置飞行模式。

3.  通过遥控器输入或地面站命令，进行控制无人机动作。

4.  计算无人机动作，算出目标电机输出，传达输出命令

                                              （图1：飞行控制流程）

         其中最主要的部分为姿态解析，这部分主要用到了飞机坐标系的旋转。转换可能有如下12种模式：

Proper Euler angles (z-x-z,x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)

Tait–Bryan angles (x-y-z,y-z-x, z-x-y, x-z-y, z-y-x, y-x-z).

       而旋转对应的方向余弦矩阵：

                                                                 图2：旋转与方向余弦矩阵

         旋转也可以通过四元数来表示：

         _{注：Roll, , About ；Pitch,} , About Y；Yaw, , About Z

1.   Roll – Pitch – Yaw Sequence, (X,Y,Z)

 

_{2.  Roll– Yaw - Pitch Sequence , (X, Z, Y)}

_3. Pitch – Roll –Yaw Sequence_{(Y, X, Z)}

_{4. Pitch – Yaw –Roll Sequence(Y, Z, X)}

5. Yaw –Roll – Pitch Sequence  (Z, X, Y)

_6. Yaw – Pitch – Roll Sequence, (Z, Y, X)

_{7.  Roll – Pitch –Roll Sequence (X, Y, X)}

_8. Roll – Yaw – Roll Sequence     (X,Z,X) 

_9. Pitch – Roll – Pitch(Y, X, Y)

_10. Pitch – Yaw – Pitch   (Y, Z, Y)   

11. Yaw –Roll – Yaw Sequence  (Z, X, Z) 

12. Yaw –Pitch – Yaw Sequence  (Z,Y,Z) 

三种选择方法的优缺点：

       欧拉角算法通过求解欧拉角微分方程直接计算航向角、俯仰角和横滚角。欧拉角微分方程关系简单明了，概念直观，容易理解，解算过程中无需作正交化处理，但方程中包含有三角运算，这给实时计算带来一定困难，而且当俯仰角接近90°时方程出现退化现象，这相当于平台惯导中惯性平台的锁定，所以这种方法只适用于水平姿态变化不大的情况，而不适用于全姿态运载体的姿态确定。

       方向余弦法对姿态矩阵微分方程做求解，避免了欧拉角法中方程的退化问题，可全姿态工作，但姿态矩阵微分方程实质上是包含9个未知量的线性微分方程组，与四元数法相比，计算量大，实时计算困难，所以工程上并不实用。

       四元数法只需求解四个未知量的线性微分方程组，计算量比方向余弦法小，且算法简单，易于操作，是较实用的工程方法。但四元数法实质上是旋转矢量法中的单子样算法，对有限转动引起的不可交换误差的补偿程度不够，所以只适用于低动态运载体（如运输机等）的姿态解算。而对高动态运载体，姿态解算中的算法漂移会十分严重。

       旋转矢量法可采用多子样算法实现对不可交换误差做有效补偿，算法关系简单，易于操作，并且通过对系数的优化处理使算法漂移在相同子样算法中达到最小，因此特别适用于角机动频繁激烈或存在严重角震动的运载体的姿态更新。

       四元数法和旋转矢量法都通过计算姿态四元数实现姿态更新，但前者直接求解姿态四元数微分方程，而后者通过求解姿态变化四元数再求解姿态四元数，两者的算法思路并不相同。

 

       解析当前姿态：

在无人机安装陀螺仪，可以测量无人机倾斜的角速度，由于陀螺仪输出的是无人机的角速度，不会受到无人机振动影响。因此该信号中噪声很小。无人机的角度又是通过对角速度积分而得，这可进一步平滑信号，从而使得角度信号更加稳定。因此四轴控制所需要的角度和角速度可以使用陀螺仪所得到的信号。由于从陀螺仪的角速度获得角度信息，需要经过积分运算。如果角速度信号存在微小的偏差，经过积分运算之后，变化形成积累误差。这个误差会随着时间延长逐步增加，最终导致电路饱和，无法形成正确的角度信号。

利用加速度计所获得的角度信息θg 与陀螺仪积分后的角度θ进行比较，将比较的误差信号经过比例Tg 放大之后与陀螺仪输出的角速度信号叠加之后再进行积分。对于加速度计给定的角度θg ，经过比例、积分环节之后产生的角度θ必然最终等于θg 。由于加速度计获得的角度信息不会存在积累误差，所以最终将输出角度θ中的积累误差消除了。加速度计所产生的角度信息θg 中会叠加很强的有运动加速度噪声信号。为了避免该信号对于角度θ的影响，因此比例系数 Tg 应该非常小。这样，加速度的噪声信号经过比例、积分后，在输出角度信息中就会非常小了。由于存在积分环节，所以无论比例Tg多么小，最终输出角度θ必然与加速度计测量的角度θg相等，只是这个调节过程会随着Tg 的减小而延长。

1.重力加速度归一化：加速度计数据归一化，把加速度计的三维向量转换为单位向量，因为是单位矢量到参考性的投影，所以要把加速度计数据单位化，其实归一化改变的只是这三个向量的长度，也就是只改变了相同的倍数，方向并没有改变，也是为了与单位四元数对应。

2.提取四元数的等效余弦矩阵中的重力分量：

将当前姿态的重力在三个轴上的分量分离出来,把四元数换算成方向余弦中的第三行的三个元素，根据余弦矩阵和欧拉角的定义，就是地理坐标系(参考坐标系)的Z轴的重力向量。

 

3.向量叉积得出姿态误差:

叉积误差是指将带有误差的加计向量转动到与重力向量重合，需要绕什么轴，转多少角度。逆向推理一下，这个叉积在机体三轴上的投影，就是加计和重力之间的角度误差。也就是说，如果陀螺按这个叉积误差的轴，转动叉积误差的角度（也就是转动三轴投影的角度）那就能把加计和重力向量的误差消除掉。（具体可看向量叉积的定义）如果完全按叉积误差转过去，那就是完全信任加计。如果一点也不转，那就是完全信任陀螺。那么把这个叉积的三轴乘以x%，加到陀螺的积分角度上去，就是这个x%互补系数的互补算法了。

4.对误差进行积分：

积分求误差,关于当前姿态分离出的重力分量,与当前加速度计测得的重力分量的差值进行积分消除误差

5.互补滤波，姿态误差补偿到角速度上，修正角速度积分漂移

系数不停地被陀螺积分更新，也不停地被误差修正，它和公式所代表的姿态也在不断更新。将积分误差反馈到陀螺仪上，修正陀螺仪的值。将该误差V_error输入 PI 控制器后与本次姿态更新周期中陀螺仪测得的角速度相加，最终得到一个修正的角速度值,将其输入四元数微分方程，更新四元数。

Gyro就是得到的修正角速度值，可以用于求解四元数q0~q3。