关于人群基数MCNN和高斯核

参考：
https://www.jianshu.com/p/a1006c4b6fdc
https://blog.csdn.net/wuyanxue/article/details/79642758

人群基数方法分类

（1） 基于目标检测的方法： 这类方法就是通过对图像上每个行人或这人头进行定位与识别，再根绝结果统计人数。优点在于可以做到准确的行人或者人头位置，但缺点在于对高密度的人群图像来说，其检测效果差；（2）基于回归的方法：这类方法可以叫做人群数目估计，没有精确定位行人位置，而是对大概的人群数目给出个估计值；优点在于对高密度人群图像来说，其效果是比基于目标检测方法的好，但缺点没有精确的定位。 基于回归的方法分为两类： 1）直接回归：如在深度学习的卷积神经网络中输入人群图像，直接输出一个人群数目估计值； 2）密度图回归：密度图回归的意思是（已知的数据集是这样的，每一张人群图像中的每个人头所在近似中心位置的坐标作为人工标注），根据已知的每个人头位置，再估计该位置所在人头的大小，这样可以得到该人头的覆盖区域，通过一种方法（MCNN中采用几何自适应高斯核），将该区域转化为该区域内可能为人头的概率，该区域概率和为1（或者表示每个像素可能有多少个人），最终我们可以得到一张人群密度图。

密度图的表示方法

密度图表示经过两个步骤：人群图像标注表示，人群图像标注转换为人群密度图（这里的描述语言是自己编的，为了更易于理解）1. 人群图像标注表示 如图1所示，19*19大小方格表示人群图像(绿色外层方格表示坐标)，该图像包含3个人，以左上角为坐标原点，坐标(3, 6), (12, 9), (17, 15)表示标注的人头中心点位置（在图1中表示为方格对应坐标的值为1）。

2. 人群密度图转换表示（人群图像标注转换为人群密度图）

假设在图像中每个人头大小都是3*3像素（当然这只是示例假设，MCNN中用几何自适应高斯核来估计图像中每个人头的大小并转换为密度图，这是后话了，这里我们想讲述的是什么是密度图，以及转换为密度图的方法之一）

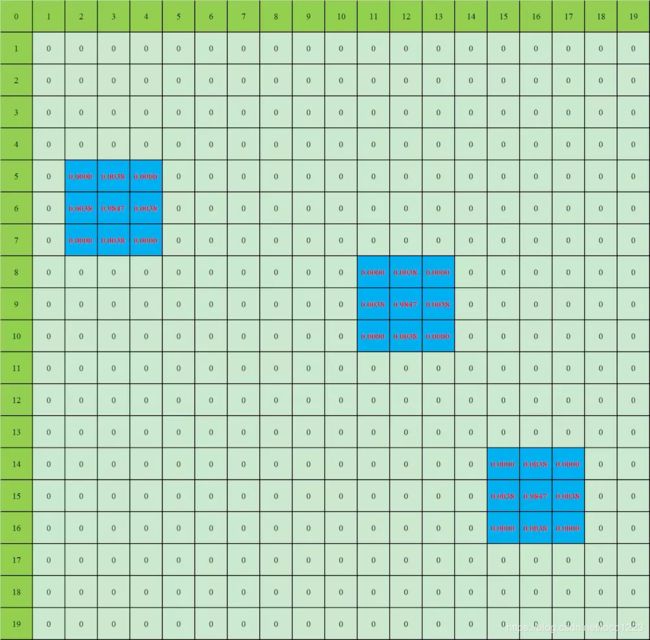
图2就是我们作为卷积神经网络进行人群计数的Ground Truth，各个人头区域的概率之和为1，得到对完整人群图像的密度图后，对其进行积分（求和）就是人群数目。

MCNN

这里我们先来描述MCNN具体的标签密度图生成方法，再来描述MCNN的网络结构和损失函数、训练方式、评价指标。1. 标签密度图生成方法 步骤a. 表示人头中心坐标位置，用函数表示，对于一张有个人头标注的人群图像来说可以表示为函数(其实得到的就是如图1的人群图像标注表示)：

步骤b. 转化为连续密度函数，其中G_{\sigma _{i}} 所表示的就是高斯核，\sigma {i}为高斯核标准差，\beta 是个定值，论文里取0.3，\bar{d} ^{i=\frac{1}{k}\sum\nolimits_{k}}jd{j}^i 表示图像中该人头距离其k邻近人头的欧式距离和的平均，\bar{d} ^i也是用于表示估计的人头大小（在图2人群密度图表示的时候，使用二维高斯核时，需要设定高斯核大小用以表示估计的人头大小）

若人群分布密集，所计算的\bar{d} ^i值能够相对准确用于估计人头大小；但若人群分布稀疏，其k近邻人头距离过远，\bar{d} ^i值就会非常大，人头估计误差大，因此将\bar{d} ^i限制在100像素内。

高斯核介绍

线性支持向量机 (Linear-SVM) 被用于线性可分的数据集的二分类问题，当数据集不是线性可分的时候，需要利用到核函数将数据集映射到高维空间。这样数据在高维空间中就线性可分。

高斯核函数（Gaussian kernel），也称径向基 (RBF) 函数，是常用的一种核函数。它可以将有限维数据映射到高维空间，我们来看一下高斯核函数的定义：

上述公式涉及到两个向量的欧式距离（2范数）计算，而且，高斯核函数是两个向量欧式距离的单调函数。σσ 是带宽，控制径向作用范围，换句话说，σσ 控制高斯核函数的局部作用范围。当xx 和x′x′ 的欧式距离处于某一个区间范围内的时候，假设固定x′x′，k(x,x′)k(x,x′) 随x的变化而变化的相当显著。

一维情况
令x′=0x′=0，k(x,0)k(x,0) 随x的变化情况如下图所示

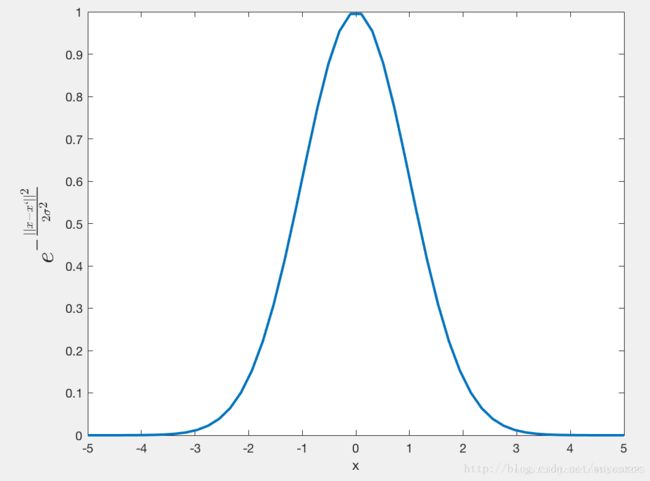
σ=1

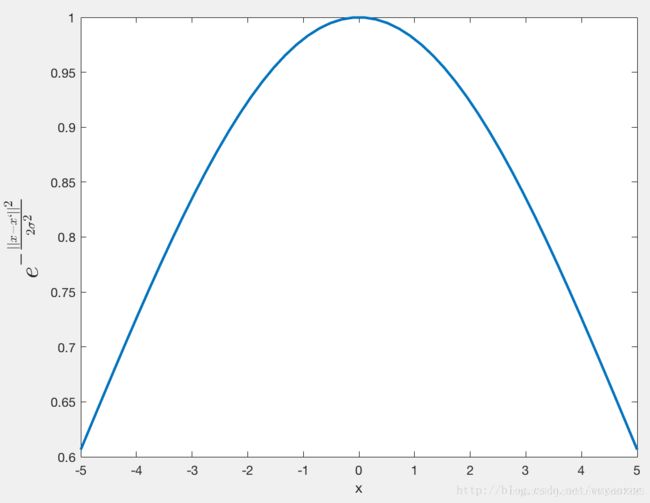
σ=5
我们看到，随着x 与x′的距离的距离的增大，其高斯核函数值在单调递减。并且，σ越大，那么高斯核函数的局部影响范围就会越大。

二维情况

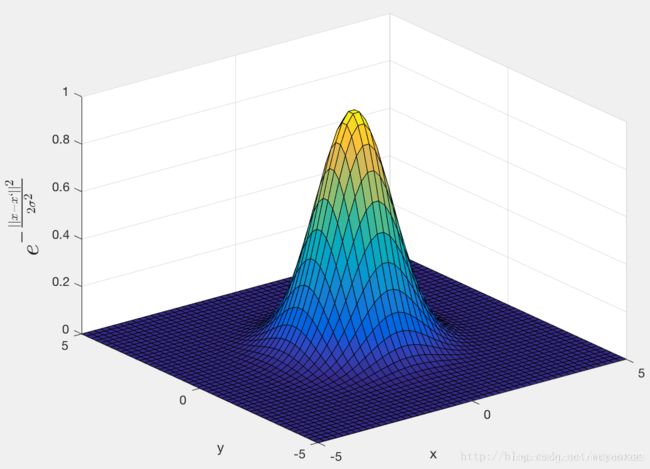
σ=1

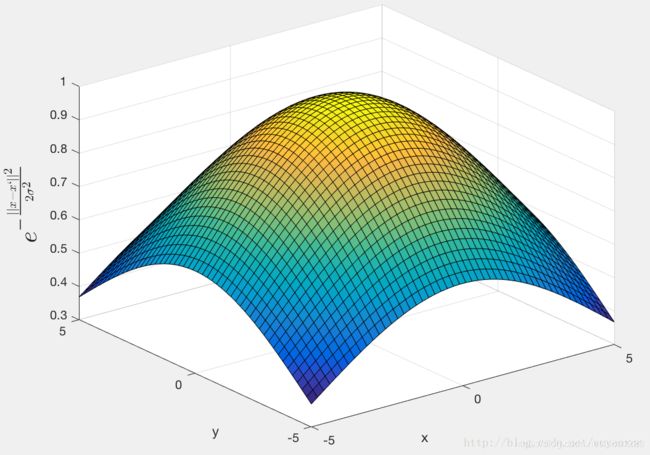
二维可以更加明显的看出高斯核函数局部作用的范围随带通的变化情况。带通越大，高斯核函数的局部影响的范围就越大。在超出这个范围之后，核函数的值几乎不变。

高斯核将数据映射到高维甚至无穷维的原理
通过一些简单的推导，我们可以得到这样的结果，为了描述简单，我们令高斯核中的分母为1

MCNN网络结构

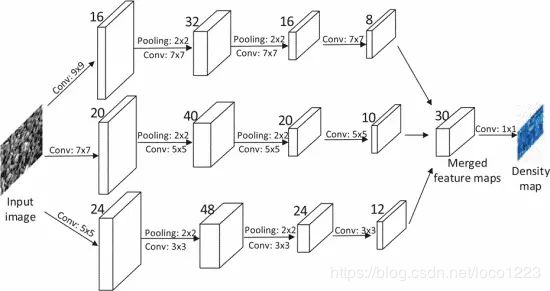
MCNN的多列主要体使用了三列卷积神经网络，表示为 L列(使用大尺度卷积核:, M列(使用中等尺度卷积核: ), S列(使用小尺度卷积核: ， 其目的在于使用多种尺度的卷积核来适应不同尺度的人头大小。最后将L,M,S三列卷积神经网络进行合并，得到网络生成的密度图。同时MCNN也是比较轻量级的，网络参数少。 从图5中可观察到，MCNN实际的下采样l累积系数为4，因此网络输出的密度图也是原图宽高的1/4，在制作其作为训练数据的标签密度图时，除了要制作为原图1/4的密度图外，几何自适应高斯核相关的的限制，也要相应为1/4，将限制在100/4=25个像素之内。

损失函数

MCNN采用的如下公式的损失函数，L2范数的平方：

训练方式

在训练方式主要想提的是： 1）MCNN需要先对三个单列神经网络进行预训练，再合并训练才能达到更好的效果其数据处理的方式； 2）MCNN对原始数据集的每张训练集图像随机裁剪9次，得到9张图像子块，每个图像子块为原图的1/4。 （这样的图像子块训练有其优点a. 图像尺寸变小，加快网络训练速度；b. 通过局部图像块的训练完成对完整图像的训练，同样能达到很好的效果）

评价指标

MCNN所采用的评价指标如下，平均绝对误差MAE与均方误差MSE(实际应该是均方根误差RMSE)