姿态篇：一.初识姿态估计

[深入浅出多旋翼飞控开发][姿态篇][一][初识姿态估计]

作者：王伟韵
QQ : 352707983
Github

一.什么是姿态

在学习姿态估计之前，我们先来了解一下，什么是 “姿态”。

想象一架飞机准备起飞，于是它在机场跑道上进行一段加速助跑，达到一定速度后，机头抬升15度，腾空而起，离开了地面。然而由于起飞时的方向和目标方向相差甚大，于是飞机调转机头，最终往北偏东30度的方向飞去。

这个过程中，根据日常生活经验，我们如此说明飞机在起飞过程中的发生的变化：“抬升15度”，“北偏东30度”。也就是说，通常我们会使用 “角度”，来表示一个物体的姿态。那这个角度大小是如何得来的？其中，“15度”指飞机机身与水平地面的夹角，“北偏东30度”则指飞行方向与正北方向的夹角。**也就是说，日常生活中我们描述物体的姿态，是以脚下的大地作为参考的。**通常人类在太空中会失去方向感，是因为地球上的重力加速度的存在让我们始终能够以大地作为参考物，而失重环境下失去了参考物，我们便无法感知自身以及周围物体的姿态了。

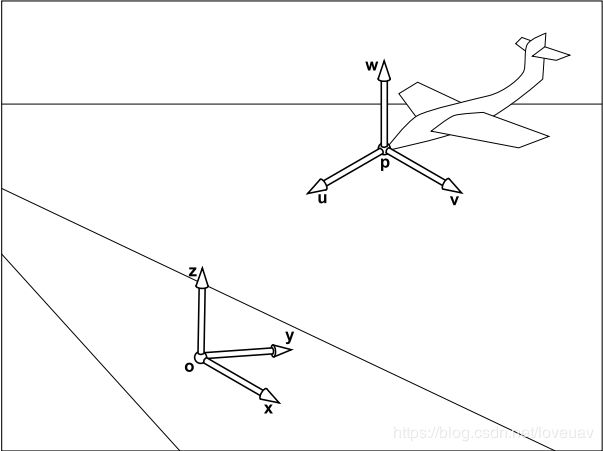
为了方便描述物体之间的方位关系，我们定义了坐标系。在上面的例子中，我们可以定义成两个坐标系，如图1：

• 大地坐标系O-xyz
• 机体坐标系P-vuw

坐标系定义

于是，我们将姿态定义为：

姿态，即表示O-xyz与P-vuw两个坐标系之间的关系。

通常，坐标系会有多个，但必须选择一个坐标系作为参考系，大部分时候我们会选取大地坐标系作为参考系，比较符合人类的直觉与习惯。

了解了姿态的定义后，我们又面临着一个问题，如何使用数学方式来描述姿态，以便下一步的计算？

二.欧拉角

欧拉角是最直观的一种姿态描述方式，其定义为：

一个坐标系到另一个坐标系的变换，可以通过绕不同坐标轴的3次连续转动来实现。这三次的转动角度统一称之为欧拉角

但有一点值得注意的是，欧拉角并不直接等同于我们常说的姿态角。

欧拉角由三次绕轴旋转组成，而这三次转动顺序任意，且转动轴可以是参考系的，也可以是机体系的，因此共有24种转动方式。

而通常飞控上所使用的姿态角，指的是航空领域主要应用的航空次序欧拉角，也叫卡尔丹角（Tait-Bryan angles），定义欧拉角的转动顺序为Z-Y-X。其中绕Z轴转动为偏航角（Yaw），绕Y轴转动为俯仰角（Pitch），绕X轴转动为横滚角（Roll），其具体意义如下：

• 偏航角（Yaw）
  机体系x轴投影到水平面与参考系x轴的夹角，顺时针旋转为正。

• 俯仰角（Pitch）
  机体系x轴与水平面的夹角，抬头为正。

• 横滚角（Roll）
  机体坐标系z轴与通过机体系x轴的铅垂面间的夹角，机体右旋为正。

图2表示了姿态欧拉角的转动方向
Z-Y-X次序欧拉角

上面提到了，欧拉角意义上并不直接等于姿态角，它只是描述了三次绕轴转动。而我们使用的姿态角：偏航角、横滚角与俯仰角实际上是机体坐标系与参考坐标系（大地坐标系）之间关系的表述。大致清楚姿态角的概念后，接下来便了解一下，如何使用传感器测量姿态角。

三.姿态的测量

1.加速度计测量俯仰与横滚角

假设飞控处于静止状态，此时加速度计仅受到重力的作用。当飞控与水平面完全平行时，此时加速度计的输出理论值为$[0,0,g]$（g为重力加速度的大小）。而当飞控以一定角度倾斜于水平面时，其输出值可能为$[0.37g,-0.5g,0.78g]$，且其模值为1g。实际上，静止状态下飞控倾斜时，加速度计所测量到的数据，便是重力加速度在机体坐标系下的投影。

于是根据加速度计的测量值与三角函数关系，我们便能计算出飞控的姿态角。不过由于偏航角定义为机体系x轴投影到水平面与参考系x轴的夹角，而重力加速度正好完全正交于水平面，因此加速度计测量值中并没有包含偏航角信息。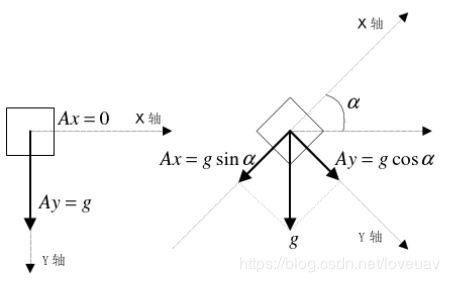
加速度与姿态角之间的三角函数关

姿态角与重力加速度投影之间的三角函数关系，这里就不具体解释了，直接给出结论，在本文的下一节中我们再从数学的角度来推导出姿态角公式。

设当前有归一化的加速度向量$a=[a_x,a_y,a_z]$，飞机横滚角为$angl{e}_x$，俯仰角为$angl{e}_y$，有如下关系：
$$\{\begin{array}{l}angl{e}_x=-arcsin(a_y)\\ angl{e}_y=arctan2(a_x,a_z)\end{array}$$

在天穹飞控的vector3.c文件中定义了AccVectorToRollPitchAngle函数来实现该转换：

void AccVectorToRollPitchAngle(Vector3f_t* angle, Vector3f_t vector)
{
	angle->x = -asinf(vector.y);            //横滚角
	angle->y = atan2f(vector.x, vector.z);  //俯仰角
}

2.磁力计测量偏航角

上面我们利用加速度计测得飞机的横滚与俯仰姿态角，但还有一个偏航角是未知的。偏航角有许多方式可以获得，但是最简单和最低成本的方式，还是通过磁力计进行测量。

假设当前有磁力计测量得到的磁场强度向量$m=[m_x,m_y,m_z]$，然后计算得到其在大地坐标系下的投影$m_n=[m_{nx},m_{ny},m_{nz}]$（具体的转换方式请阅下一节）。

设飞机的偏航角为$angl{e}_z$，有：
$$angl{e}_z=-arctan2(m_{ny},m_{nx})$$

该公式的推导请参阅下节。同样，在天穹飞控中定义了MagVectorToYawAngle函数来实现该转换：

void MagVectorToYawAngle(Vector3f_t* angle, Vector3f_t vector)
{
	angle->z = -atan2f(vector.y, vector.x);     //偏航角
}

3.关于陀螺仪

至此，我们已经了解完毕如何使用加速度计和磁力计来测量飞机的姿态角。但你可能发现，飞控中最重要的一个传感器：陀螺仪，还没有登场。既然使用上述两个传感器就已经能得到飞机的姿态，那还需要陀螺仪做什么呢？

实际上，使用加速度计和磁力计计算姿态的前提是，飞机处于一个理想的静止状态下。然而现实中这是不可能的，那么当飞机处于飞行状态时，加速度计测量得到的数据，便不仅仅是重力加速度了，可能还包含了飞行过程中所产生的运动加速度，以及一些有害加速度，通常由于机身震动，还会引入额外的震动噪声（也属于线性加速度）。此时直接使用加速度数据计算姿态，最终得到的是带有了巨大误差以及噪声的值，对于飞控来说是完全不可用的。同样，磁力计的实际测量噪声一般也比较大，而且在许多环境下还会存在磁场干扰，从而导致直接使用磁力计计算出来的偏航角存在大量误差而不可用。

而陀螺仪是一种可以测量旋转角速度的传感器，对角速度值进行离散化数值积分，便得到某段时间内的姿态变化量，这就是我们使用陀螺仪来计算飞机姿态的方式。但需要注意，使用陀螺仪只能计算出飞机姿态的相对变化量，而无法直接测量绝对姿态值，因此使用陀螺仪来更新飞机姿态时，必须先得知初始姿态值。

相比加速度计和磁力计，陀螺仪几乎不受外界环境干扰，且对线性加速度（震动）不敏感，这些特性使得陀螺仪成为了飞行器中最核心的传感器，甚至在某些极端情况下（比如火箭的起飞加速阶段），只有陀螺仪可用，这时陀螺仪的精度便至关重要了。实际上，尽管陀螺仪拥有如此优秀的特性，却也不是完美的，自身会存在各种误差，而在角速度积分阶段，陀螺仪误差会被累积，从而使得姿态逐渐偏离真实值。

经验告诉我们，使用单一传感器来计算获取飞机的姿态是不现实的，所以实际应用中，需要同时使用多种传感器来计算姿态。上面我们已经了解了使用加速度计和磁力计来计算姿态角的方法，下面便接着学习如何使用陀螺仪来更新姿态。在这之前，必须要先介绍姿态的另一种描述方式：方向余弦矩阵。

四.方向余弦矩阵

1.方向余弦矩阵的定义

第二节中我们定义姿态欧拉角的转动顺序为Z-Y-X。

根据天穹飞控中坐标系和旋转方向的定义，将姿态角的单次转动转化为矩阵的形式，有：

• 绕Z轴转动（偏航角$z$）的旋转矩阵

$$C_z=\left[\begin{array}{cccc}cosz& sinz& 0& \\ -sinz& cosz& 0& \\ 0& 0& 1& \end{array}\right]$$

• 绕Y轴转动（俯仰角$y$）的旋转矩阵

$$C_y=\left[\begin{array}{cccc}cosy& 0& siny& \\ 0& 1& 0& \\ -siny& 0& cosy& \end{array}\right]$$

• 绕X轴转动（横滚角$x$）的旋转矩阵
  $$C_x=\left[\begin{array}{cccc}1& 0& 0& \\ 0& cosx& -sinx& \\ 0& sinx& cosx& \end{array}\right]$$

将上面的3个旋转矩阵以Z-Y-X的转动顺序进行连乘，我们便得到了一个可以表示此次欧拉转动的旋转矩阵$C$，计算过程如下：

$$C=C_z\ast C_y\ast C_x$$
$$=\left[\begin{array}{cccc}cosz& sinz& 0& \\ -sinz& cosz& 0& \\ 0& 0& 1& \end{array}\right]\left[\begin{array}{cccc}cosy& 0& siny& \\ 0& 1& 0& \\ -siny& 0& cosy& \end{array}\right]\left[\begin{array}{cccc}1& 0& 0& \\ 0& cosx& -sinx& \\ 0& sinx& cosx& \end{array}\right]$$
$$=\left[\begin{array}{cccc}coszcosy& sinz& coszsiny& \\ -sinzcosy& cosz& -sinzsiny& \\ -siny& 0& cosy& \end{array}\right]\left[\begin{array}{cccc}1& 0& 0& \\ 0& cosx& -sinx& \\ 0& sinx& cosx& \end{array}\right]$$
$$=\left[\begin{array}{cccc}cosycosz& sinzcosx+sinxsinycosz& -sinxsinz+sinycosxcosz& \\ -sinzcosy& cosxcosz-sinxsinysinz& -sinxcosz-sinysinzcosx& \\ -siny& sinxcosy& cosxcosy& \end{array}\right]$$

旋转矩阵$C$，也被称之为方向余弦矩阵（Direction Cosine Matrix，简称DCM），同样可用于表示两个坐标系之间的关系。这里的方向余弦矩阵$C$，实际上描述了从参考系到机体系的转动。

由于转动顺序以及转动轴的不一致，DCM的最终表示形式会有很多种，所以在网上看到的DCM公式各不一致，实际使用中要根据坐标系的定义及欧拉角的旋转次序来计算DCM。

利用小角度近似简化方向余弦矩阵

当旋转角足够小时，根据三角函数的小角度近似关系，有：
$$\{\begin{array}{l}sin\theta \approx \theta \\ cos\theta \approx 1\end{array}$$
并忽略小角度连乘，可以得到方向余弦矩阵的简化形式
$$C=\left[\begin{array}{cccc}1& z& y& \\ -z& 1& -x& \\ -y& x& 1& \end{array}\right]$$

当然这样会损失一定的计算精度，且只能在角度变化量较小时使用。过去由于单片机资源有限，运行速度较慢，因此在许多8位机上会选择使用该简化版的DCM，以节省大量运算时间（三角函数运算比较费时）。而现在飞控主控的运行速度已经足够快，这种用法已经很少见了。

欧拉角转换为方向余弦矩阵

在方向余弦矩阵的定义中可以得到使用欧拉角转化为方向余弦矩阵的计算公式。在天穹飞控中，定义了 EulerAngleToDCM 函数：

void EulerAngleToDCM(Vector3f_t angle, float* dcM)
{
    Vector3f_t cos, sin;
    
    cos.x = cosf(angle.x);
    cos.y = cosf(angle.y);
    cos.z = cosf(angle.z);   
    sin.x = sinf(angle.x);
    sin.y = sinf(angle.y);
    sin.z = sinf(angle.z);    

    dcM[0] = cos.y * cos.z; 
    dcM[1] = sin.z * cos.x + sin.x * sin.y * cos.z; 
    dcM[2] = -sin.x * sin.z + sin.y * cos.x * cos.z; 
    dcM[3] = -sin.z * cos.y;
    dcM[4] = cos.x * cos.z - sin.x * sin.y * sin.z;
    dcM[5] = -sin.x * cos.z - sin.y * sin.z * cos.x; 
    dcM[6] = -sin.y;
    dcM[7] = sin.x * cos.y;
    dcM[8] = cos.x * cos.y;
}

该函数将欧拉角转换为了方向余弦矩阵，其角度输入值可以是某段时间内的由陀螺仪测量到的角度变化量，也可以是当前飞机的姿态角。

2.方向余弦矩阵的使用举例

从参考系到机体系

已知参考系下的加速度向量$A_n=[0,0,g{]}^T$，当前飞机姿态角分别为
$$\{\begin{array}{l}x（横滚角）\\ y（俯仰角）\\ z（偏航角）\end{array}$$

定义表示从参考系旋转到机体系的方向余弦矩阵为$C_n^b$，那么我们便能计算得到参考系加速度向量在机体系下的投影$A_b$：
$$A_b=C_n^b\ast A_n$$

其中
$$C_n^b=\left[\begin{array}{cccc}cosycosz& sinzcosx+sinxsinycosz& -sinxsinz+sinycosxcosz& \\ -sinzcosy& cosxcosz-sinxsinysinz& -sinxcosz-sinysinzcosx& \\ -siny& sinxcosy& cosxcosy& \end{array}\right]$$

同样在天穹飞控的vector3.c文件中，定义了VectorRotateToBodyFrame函数，用于转换向量至机体坐标系：

Vector3f_t VectorRotateToBodyFrame(Vector3f_t vector, Vector3f_t deltaAngle)
{
    float dcMat[9];

    //欧拉角转为方向余弦矩阵
    EulerAngleToDCM(deltaAngle, dcMat);

    //方向余弦矩阵乘以向量，得到旋转后的新向量
    return Matrix3MulVector3(dcMat, vector);
}

从机体系到参考系

已知参考系的加速度向量在机体下的投影$A_b=[0.2g,0.3g,0.9g{]}^T$（在飞控中即为加速度传感器的测量值），当前飞机姿态角为$x,y,z$，定义表示从机体系旋转到参考系的方向余弦矩阵为$C_b^n$，因此可以计算得到原参考系下的加速度向量$A_n$：
$$A_n=C_b^n\ast A_b$$

可以看出，$ C_b^n $等于从参考系旋转到机体系的方向余弦矩阵$C_n^b$的转置，即：
$$C_b^n=(C_n^b{)}^T$$
$$=\left[\begin{array}{cccc}cosycosz& -sinzcosy& -siny& \\ sinzcosx+sinxsinycosz& cosxcosz-sinxsinysinz& sinxcosy& \\ -sinxsinz+sinycosxcosz& -sinxcosz-sinysinzcosx& cosxcosy& \end{array}\right]$$

在vector3.c中，定义了函数VectorRotateToEarthFrame，用于转换向量至参考系（大地坐标系）：

Vector3f_t VectorRotateToEarthFrame(Vector3f_t vector, Vector3f_t deltaAngle)
{
    float dcMat[9];

    //欧拉角转为方向余弦矩阵
    EulerAngleToDCM_T(deltaAngle, dcMat);

    //方向余弦矩阵乘以向量，得到旋转后的新向量
    return Matrix3MulVector3(dcMat, vector);
}

注意函数中使用的是欧拉角构建的方向余弦矩阵的转置。

3.利用方向余弦矩阵推导姿态角公式

横滚与俯仰角

设静止状态下加速度计测量到的加速度向量为$A_b$，并对其归一化，有$A_b=[a_x,a_y,a_z{]}^T$，$A_n$为参考系下的归一化重力加速度向量，有$A_n=[0,0,1{]}^T$，由第二小节中的方向余弦矩阵旋转关系，即：
$$A_b=C_n^b\ast A_n$$
可得：
$$\left[\begin{array}{c}{a}_x\\ a_y\\ a_z\end{array}\right]=\left[\begin{array}{cccc}cosycosz& sinzcosx+sinxsinycosz& -sinxsinz+sinycosxcosz& \\ -sinzcosy& cosxcosz-sinxsinysinz& -sinxcosz-sinysinzcosx& \\ -siny& sinxcosy& cosxcosy& \end{array}\right]\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$$

从而得到以下关系：
$$\{\begin{array}{l}{a}_x=-sinxsinz+sinycosxcosz\\ a_y=-sinxcosz-sinysinzcosx\\ a_z=cosxcosy\end{array}$$
其中，z（偏航角）为无关变量（绕z轴的任意旋转都不会改变重力加速度向量），因此$z=0$，对上式化简可得：
$$\{\begin{array}{l}{a}_x=sinycosx\\ a_y=-sinx\\ a_z=cosxcosy\end{array}$$

即：$a_x/a_z=tany$，$a_y=-sinx$，于是我们得到了横滚与俯仰角的计算公式：
$$\{\begin{array}{l}angl{e}_x=-arcsin(a_y)\\ angl{e}_y=arctan2(a_x,a_z)\end{array}$$

偏航角

推导方式类似，不同的是参考系下的归一化地磁场向量为$M_n=[1,0,0{]}^T$，利用同样的转换关系，可以得到：
$$\{\begin{array}{l}{m}_{nx}=cosycosz\\ m_{ny}=-sinzcosy\\ m_{nz}=-siny\end{array}$$

即：$m_y/m_x=-tanz$，从而得出偏航角的计算公式为：
$$angl{e}_z=-arctan2(m_y,m_x)$$

到这里便结束了？并没有。
与使用加速度向量计算横滚俯仰角不一样的是，上面计算所使用的$m_{nx},m_{ny},m_{nz}$，并非磁力计的原始测量数据。原因是在姿态角的旋转顺序定义Z-Y-X中，偏航角是最先发生旋转的，此时地磁场向量仍与水平面平行，即该向量实则为机体系磁场向量在水平面上的投影，设为$m_n$，设机体系下的地磁场向量为$m$（磁力计的测量值），有如下关系：
$$m_n=C_b^n\ast m=(C_n^b{)}^T\ast m$$
其中$C_n^b$ 为由当前姿态角$x,y,z$（z=0）构成的方向余弦矩阵。这一步实则为地磁场向量的坐标系转换，在网上的许多相关资料中被描述为“倾斜补偿”。

五.姿态更新

上一节中我们了解了方向余弦矩阵的基本定义及其使用方法，本节中将重点讲解，如何通过方向余弦矩阵的方式，使用陀螺仪数据进行姿态更新。

1.数值积分

学习过高中物理的童鞋，对积分的概念肯定比较熟悉。已知一个速度$v$与时间$t$的相关函数$f(v,t)$，在某时间段内对其积分，有$s={\int }_{t0}^{t1}f(v,t)$，s即为t0到t1时刻的位移。在该式子中，我们需要求得$f(v,t)$的定积分公式，然后代入$t_0$和$t_1$，求出s。

然而在现实中，绝大部分函数是无法得出其定积分公式的，所以通常我们使用数值逼近的方法来计算给定函数的定积分值。

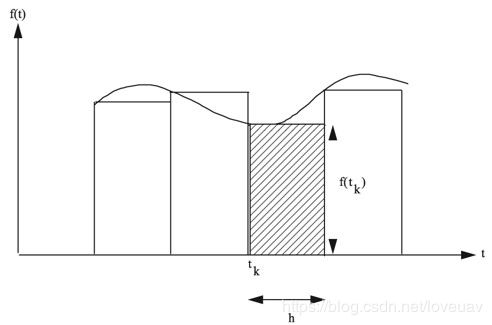
一阶矩形积分

设有一角度函数$\theta$，其微分方程为：
$${\theta }^{\prime }=f(\omega ,t)$$
$f(\omega ,t)$即为角速度$\omega$对时间$t$的相关函数。

从微积分学中得知微分方程的定义可以被近似为：
$${\theta }^{\prime }=f(\omega ,t)=\frac{\theta (t+h)-\theta (t)}{h}=\frac{{\theta }_k-{\theta }_{k-1}}{h}（当h足够小时）$$
重新整理形式，可得：
$${\theta }_k={\theta }_{k-1}+h\ast f(\omega ,t)$$
这便是一阶积分的公式，其几何意义如下图。可以看出，一阶积分实际上等同于将原函数分解成无数个宽度为固定时间间隔$h$，高度为$f(\omega ,t)$的矩形，然后计算这些矩形的面积并求和，从而得到了原函数的积分近似值。选取的时间间隔$h$越小，积分精度越高。

一阶矩形积分的几何意义

二阶梯形积分

对于上述例子，可以得到另一种微分方程的近似形式：
$${\theta }_k={\theta }_{k-1}+0.5\ast h\ast (f(\omega ,t)+f(\omega ,t+h))$$
其几何意义如下图。

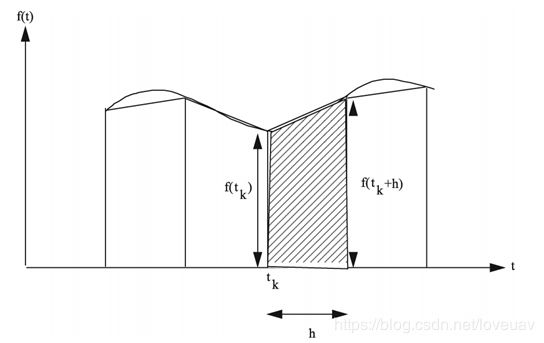
二阶梯形积分的几何意义

明显可以看出这种对梯形求面积的二阶积分方式的精度要高于一阶矩形积分。

积分方式的选择

上面我们了解到了两种数值积分方式：一阶矩形积分和二阶梯形积分。实际上它们还有另一种叫法：一阶龙格库塔积分和二阶龙格库塔积分，往上还有更高阶数的龙格库塔积分算法。

显然，对于特定方程以及同等积分步长$h$，使用高阶数的龙格库塔法可以得到更高的积分精度。然而在天穹飞控中，我们选择使用一阶积分，这是因为使用较高的积分频率（积分步长$h$很小）如1000Hz时，其积分效果实测基本完全一致。原因是此时传感器自身的误差已经远远大于不同积分算法所带来的误差。

2.使用陀螺仪更新姿态

设有陀螺仪在某时刻的角速度采样值$\omega =({\omega }_x,{\omega }_y,{\omega }_z)$，采样时间间隔为$\Delta t$，使用一阶积分算法，可以得到$\Delta t$间隔内的角度变化量为：
$$\{\begin{array}{l}\Delta x={\omega }_x\ast \Delta t\\ \Delta y={\omega }_y\ast \Delta t\\ \Delta z={\omega }_z\ast \Delta t\end{array}$$

于是可以得到一个描述物体在$\Delta t$间隔内的转动的方向余弦矩阵$C_{\Delta t}$：
$$C_{\Delta t}=\left[\begin{array}{cccc}cos\Delta ycos\Delta z& sin\Delta zcos\Delta x+sin\Delta xsin\Delta ycos\Delta z& -sin\Delta xsin\Delta z+sin\Delta ycos\Delta xcos\Delta z& \\ -sin\Delta zcos\Delta y& cos\Delta xcos\Delta z-sin\Delta xsin\Delta ysin\Delta z& -sin\Delta xcos\Delta z-sin\Delta ysin\Delta zcos\Delta x& \\ -sin\Delta y& sin\Delta xcos\Delta y& cos\Delta xcos\Delta y& \end{array}\right]$$

有上节中方向余弦矩阵的使用方式得知，我们可以使用$C_{\Delta t}$对一个三维向量或者描述当前姿态的方向余弦矩阵进行更新，从而实现了使用陀螺仪测量得到的角速度数据对姿态进行更新这一目的。

例如：

设$A_t=[a_x,a_y,a_z{]}^T$ 为t时刻重力加速度向量在机体坐标系下的投影，在$\Delta t$间隔内发送了一次转动，得到了下一时刻的重力加速度向量投影$A_{t+1}$ ，即：
$$A_{t+1}=C_{\Delta t}\ast A_t$$

该式即为姿态的迭代公式，使用每一个新时刻地角速度数据进行迭代计算，便能不断地获取到新的姿态值。不过这里的$A_t$只包含了俯仰与横滚角信息，同理如果我们需要得到偏航角，只需定义一个向量为地磁场向量投影，然后使用$C_{\Delta t}$对其进行迭代更新即可。

下面给出一个使用陀螺仪更新姿态的代码示例：

void AttitudeUpdate(Vector3f_t gyro, float deltaT)
{
    Vector3f_t deltaAngle;   
    static Vector3f_t vectorG = {0, 0, 1};     //定义重力加速度向量投影并初始化
    static Vector3f_t vectorM = {1, 0, 0};     //定义地磁场向量投影并初始化  
    float  dcMat[9];                           //方向余弦矩阵
    static Vector3f_t angle;                   //姿态角
    
    //一阶积分计算角度变化量，单位为弧度
    //gyro为角速度数据，单位为°/s，deltaT为该函数的运行时间间隔，单位为s
	deltaAngle.x = Radians(gyro.x * deltaT); 
	deltaAngle.y = Radians(gyro.y * deltaT); 
	deltaAngle.z = Radians(gyro.z * deltaT); 
    
    //角度变化量转换为方向余弦矩阵
    EulerAngleToDCM(deltaAngle, dcMat);
    
    //更新姿态向量 vector = DCM * vector
    vectorG = Matrix3MulVector3(dcMat, vectorG);
    vectorM = Matrix3MulVector3(dcMat, vectorM);
    
    //计算俯仰与横滚角，并由弧度制转为角度制
    AccVectorToRollPitchAngle(&angle, vectorG);   
	angle.x = Degrees(angle.x);
	angle.y = Degrees(angle.y);    

	//转换地磁场向量投影到参考系的水平面
    Vector3f_t vectorM_Ef;
	BodyFrameToEarthFrame(angle, vectorM, &vectorM_Ef);
    
    //计算偏航角，并由弧度制转为角度制
    MagVectorToYawAngle(&angle, vectorM_Ef);
	angle.z = Degrees(angle.z);    
    
    //将偏航角限制为0-360°
    angle.z = WrapDegree360(angle.z);    
}

3.姿态的初始对准

前面提过，使用陀螺仪更新姿态，有一个前提是需要先获得姿态的初始值。在上面的代码实例中，我们直接在变量初始化中给了一个初始值，假定初始状态为机体系与参考系完全贴合。但实际应用中，在飞控刚上电时，我们必须对姿态的状态量进行初始化。最简单直接的方法便是多次读取加速度计与磁力计的值，然后求平均值，把最终得到的数据作为姿态的初始值。

在天穹飞控中定义了 AttitudeInitAlignment 函数用于姿态初始化。

4.传感器校准

在飞控中运行第二小节中给出的姿态更新示例，你会发现，尽管计算出来的姿态值能够很好的反映飞控的真实姿态变化，但依然存在着一个很大的问题：当飞控静止不动时，姿态值仍然在不断变化，随着时间的增加，姿态值与飞控的真实姿态之间的误差会越来越大。

这是因为陀螺仪传感器本身存在着误差。飞控静止时，理论上陀螺仪的输出为0，即角速度为0，姿态不变。但实际上即使在静止状态，陀螺仪依然会有输出，这称之为陀螺仪的零偏误差，姿态更新过程中，零偏误差也会不断被累积，最终误差越来越大，使得姿态值逐渐偏离真实值。

为了解决这个问题，需要对传感器进行校准，减小甚至消除其误差。对于陀螺仪来说，校准零偏误差的最简单方式，便是将飞控静止放置，在一定时间内连续读取其输出，然后取平均值，得到的数据即为零偏误差。在后面的姿态更新中，角速度值减去该零偏误差即可。

实际上陀螺仪的误差组成并非如此简单，要取得较好的校准效果需要花费很多功夫，且要有额外设备的支持。另外其余传感器如加速度计和磁力计，也均需要校准，其具体校准实现颇为复杂，这里不便展开，在本教程的【姿态篇】的第四篇中，将进行详细讲述。有兴趣的童鞋可前往查看：姿态篇：四.非线性最小二乘与飞控传感器校准。

经过校准后，陀螺仪误差将极大减小，但是并非代表完全不存在误差。事实上，陀螺仪的零偏误差并不会固定不变，而是会随着环境、温度、时间等因素的变化而变化，这就带来了很多麻烦。另外通常多旋翼飞控上使用的均为低成本MEMS陀螺仪，其随机噪声误差也非常大。这就表示，陀螺仪没有误差的理想情况在现实中是不可能存在的。因此单独使用陀螺仪来更新姿态，其误差会逐渐累积，无法长时间保证姿态值的准确。

下一节中，我们将介绍如何使用多传感器融合的方式，计算出尽可能准确的姿态值。

六.姿态估计与互补滤波

估计，其意为对事物做出大致的推断。某一天下班后路过一个水果摊，突然想买点龙眼解解馋，可是囊中羞涩，支付宝上的余额大约只能买2到3斤。于是找老板要了个袋子，挑了许多龙眼，大概用手感觉了一下，应该有2斤。这时候我对龙眼重量的猜测，便是估计值。然后给老板放到秤上一秤，2.3斤，这是真实值。而2.3 - 2 = 0.3，则是这个过程中的估计误差。

而对于飞控而言的姿态估计，便是计算出一个最接近真实值的姿态值，也就是让估计误差最小。姿态的测量与计算，离不开传感器，但是各种传感器均存在不同的优缺点，其中：

• 陀螺仪可用于姿态的连续更新，优点是精度较高且几乎不受外界因素干扰，缺点是自身存在误差，在积分阶段会因为误差不断累积从而使得计算结果不准确。

• 加速度计和磁力计可直接用于姿态的测量，优点是绝对准确，不存在累积误差，但缺点也很明显，容易受到干扰。另外加速度计容易受到震动影响，并且对姿态的测量结果仅在静止或者物体匀速运动时才准确。

单一使用任何传感器，都无法得到有效准确的姿态信息。因此，我们需要同时使用多个传感器，结合各自优缺点，将其数据进行融合，从而得到最准确的估计。

其中，多传感器信息融合的最有效的一种方式为加权融合。而通常用于融合的多个传感器之间存在性质互补的情况，所以我们也称之为互补滤波。尽管名字中带有“滤波”两字，却完全不同于传统意义上的对某信号特定频域上进行滤除操作的滤波，实则上它是一种最优估计方法。

定义如下式子：
$$angl{e}_{t+1}=(1-k)\ast (angl{e}_t+{\omega }_t\ast \Delta t)+k\ast angl{e}_{measure}$$

这就是一个简单的使用互补滤波更新姿态的示例。其中$angl{e}_t$和$angl{e}_{t+1}$分别为$t$，$t+1$时刻的姿态角估计值，${\omega }_t$为$t$时刻的角速度，$angl{e}_{measure}$为$t$时刻来至于加速度计或磁力计的姿态测量值。

其中的$k$，便是最核心的权重因子了。它的大小决定了$t$时刻的估计中，我们相信哪个传感器的数据多一点。比如$k=0.001$，则有$1-k=0.999$，意味着在每一次估计中，角速度所更新的姿态值要远比来自加速度（或磁力计）的姿态测量值准确，但同时还是使用了姿态测量值对姿态进行修正，以消除角速度积分带来的累积误差。这样，我们便得到了一个相对而言更准确的姿态估计：对外界环境因素的干扰不敏感，也不会因为角速度积分累积误差而逐渐偏离真实值。

对上式进行分解和变换，可以得到：
$$\{\begin{array}{l}angl{e}_t=angl{e}_t+{\omega }_t\ast \Delta t\\ angl{e}_{t+1}=angl{e}_t+k\ast (angl{e}_{measure}-angl{e}_t)\end{array}$$

即先使用角速度数据更新姿态，然后使用姿态观测值对姿态估计值进行修正，修正速度取决于$k$的大小。

在上节使用角速度更新姿态的例子中，有：
$$A_{t+1}=C_{\Delta t}\ast A_t$$

定义t时刻的加速度观测为$a_t$，可以得到：
$$\{\begin{array}{l}{A}_t^{-}=C_{\Delta t}\ast A_t\\ A_{t+1}=A_t^{-}+K\ast (a_t-A_t^{-})\end{array}$$

其中$K$是一个对角线元素为权重因子的3x3矩阵，即：
$$K=\left[\begin{array}{cccc}{k}_1& 0& 0& \\ 0& k_2& 0& \\ 0& 0& k_3& \end{array}\right]$$

下面贴上在上一节的角速度更新姿态代码基础上加入互补滤波的程序实例：

void AttitudeUpdateByComplementaryFilter(Vector3f_t gyro, Vector3f_t acc, Vector3f_t mag, float deltaT)
{
    Vector3f_t deltaAngle;   
    static Vector3f_t vectorG = {0, 0, 1};     //定义重力加速度向量投影并初始化
    static Vector3f_t vectorM = {1, 0, 0};     //定义地磁场向量投影并初始化  
    float  dcMat[9];                           //方向余弦矩阵
    static Vector3f_t angle;                   //姿态角
    
    static float K_G[9] = {0.0003, 0, 0, 0, 0.0003, 0, 0, 0, 0.0003};  //重力加速度向量的互补滤波权重矩阵
    static float K_M[9] = {0.001, 0, 0, 0, 0.001, 0, 0, 0, 0.001};     //地磁场向量的互补滤波权重矩阵
    
    //一阶积分计算角度变化量，单位为弧度
    //gyro为角速度数据，单位为°/s，deltaT为该函数的运行时间间隔，单位为s
    deltaAngle.x = Radians(gyro.x * deltaT); 
    deltaAngle.y = Radians(gyro.y * deltaT); 
    deltaAngle.z = Radians(gyro.z * deltaT); 
    
    //角度变化量转换为方向余弦矩阵
    EulerAngleToDCM(deltaAngle, dcMat);
    
    //更新姿态向量 vector = DCM * vector
    vectorG = Matrix3MulVector3(dcMat, vectorG);
    vectorM = Matrix3MulVector3(dcMat, vectorM);
    
    //使用互补滤波对姿态估计量进行修正
    //acc为加速度计测量值，mag为磁力计测量值
    vectorG = Vector3f_Add(vectorG, Matrix3MulVector3(K_G, Vector3f_Sub(acc, vectorG)));
    vectorM = Vector3f_Add(vectorM, Matrix3MulVector3(K_M, Vector3f_Sub(mag, vectorM)));
    
    //计算俯仰与横滚角，并由弧度制转为角度制
    AccVectorToRollPitchAngle(&angle, vectorG);   
    angle.x = Degrees(angle.x);
    angle.y = Degrees(angle.y);    

    //转换地磁场向量投影到参考系的水平面
    Vector3f_t vectorM_Ef;
    BodyFrameToEarthFrame(angle, vectorM, &vectorM_Ef);
    
    //计算偏航角，并由弧度制转为角度制
    MagVectorToYawAngle(&angle, vectorM_Ef);
    angle.z = Degrees(angle.z);    
    
    //将偏航角限制为0-360°
    angle.z = WrapDegree360(angle.z);    
}

其中Vector3f_Add和Matrix3MulVector3为天穹飞控中定义的各类向量及矩阵运算函数，详情请参阅Math文件夹下的代码：天穹飞控

七.代码与工程实例

本节中将给出一个具体的工程实例，可以直接在天穹飞控的硬件上进行运行和调试，帮助初学者对本篇内容的学习和理解。

后续再更新。

八.总结

本篇文章介绍了姿态的基本定义和表示方式，并讲解了多种传感器计算姿态的方法，以及使用多传感器融合估计姿态的一种基本算法。结合有大量代码实例，可以帮助初学者入门，如果依然有不明白的地方，可以上论坛或者Q群提问，也可以同时结合Github上的天穹飞控的代码进行学习。

这里是传送门：

天穹飞控
飞控交流论坛
飞控交流Q群：472648354

作为本教程姿态篇的开篇及入门篇，仅仅是介绍了一些基本概念及算法，然而实际环境颇为复杂，需要考虑的因素非常多，要提高姿态估计的精度，还有很长的路要走。最后用于多传感器融合的互补滤波算法中，其权重因子通常依靠调试和经验给出。而下一节我们将会学习卡尔曼滤波，一种从概率角度计算融合权重的最优估计方法，顺便介绍另一种常见的姿态表示方式：四元数。