树状数组
参考博文:http://blog.csdn.net/int64ago/article/details/7429868
1. 树状数组的功能
平常我们会遇到一些对数组进行维护查询的操作,例如修改某点的值、求某个区间的和。当数据规模不大的时候,对于修改某点的值是非常容易的,复杂度是O(1),但是对于求一个区间的和就要扫一遍了,复杂度是O(N),如果实时的对数组进行M次修改再求和,最坏的情况下复杂度是O(M*N),当规模增大后速度很慢。
2. 树状数组的实现
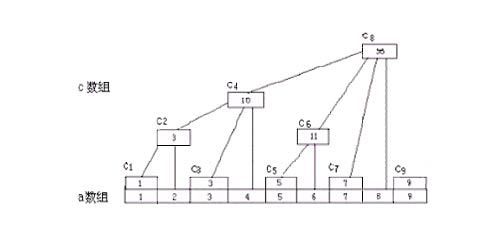
下面的说明都是基于这两幅图的,左边的叫A图,右边的叫B图
图A有两个数组,a数组存储的是原始数组值,c数组存储的是部分区间和值。下面介绍c数组计算规则,从图中可以很清楚的看到c1 = a1, c2 = a2 + a1, c4 = a4 + a3 + a2 + a1, c[i]的计算规则是从a[i]开始连续(i的二进制低位1组成的数)个数之和。下面介绍一个定义,解释什么是i的二进制低位1组成的数以及如何计算。
定义一:数值k的二进制低位1组成的数通过lowbit(k)来计算,lowbit(k)就是把k的二进制的高位1全部清空,只留下最低位的1,比如10的二进制是1010,则lowbit(k)=lowbit(1010)=0010(2进制),介于这个lowbit在下面会经常用到,这里给一个非常方便的实现方式,比较普遍的方法lowbit(k)=k&-k,这是位运算,我们知道一个数加一个负号是把这个数的二进制取反+1,如-10的二进制就是-1010=0101+1=0110,然后用1010&0110,答案就是0010了。
因此下标4的二进制是100, 100(二进制)lowbit(k)值为100(二进制)转化为十进制就是4,因此 c4 为从a4开始,求连续4个数的和,故c4 = a4 + a3 + a2 + a1, 同理下标3的二进制是11,它的lowbit值为1,故c3 = a3。c8 = a8 + a7 + a6 + a5 + a4 + a3 + a2 + a1。为什么要这样计算呢,其实c8 = c4 + c6 + c7 + a8,可以看做 a1~a8的左半边和+右半边和。左边和a1~a4已经计算完成为c4, 右边和a5~a8可以按照同样的规则一分为二,转化为左半边和a5~a6(c6)+后半边和a7~a8,通过二分的方法将求和的时间复杂度减低到log(n)。
下面介绍数状数组需要执行的两个操作。
1. 修改a数组某一项值
a数组每次修改都需要维护c数组应有的性质,因为后面求和要用到。而维护也很简单,比如更改了a[0011],我们接着要修改c[0011],c[0100],c[1000],这是很容易从图上看出来的,那么他们之间有什么必然联系呢?其实从0011——>0100——>1000的变化都是进行“去尾”操作,就是把尾部应该去掉的1都去掉转而换到更高位的1,记住每次变换都要有一个高位的1产生,所以0100是不能变换到0101的,因为没有新的高位1产生,这个变换过程恰好是可以借助我们的lowbit进行的,k +=lowbit(k)。
为什么它非要是这种关系啊?这就要追究到之前我们说c8可以看作a1~a8的左半边和+右半边和……的内容了,为什么c[0011]会影响到c[0100]而不会影响到c[0101],这就是之前说的c[0100]的求解实际上是这样分段的区间 c[0001]~c[0001] 和区间c[0011]~c[0011]的和,数字太小,可能这样不太理解,在比如c[0100]会影响c[1000],为什么呢?因为c[1000]可以看作0001~0100的和加上0101~1000的和,但是0101位置的数变化并会直接作用于c[1000],因为它的尾部1不能一下在跳两级在产生两次高位1,是通过c[0110]间接影响的,但是,c[0100]却可以跳一级产生一次高位1。
可能上面说的你比较绕了,那么此时你只需注意:c的构成性质(其实是分组性质)决定了c[0011]只会直接影响c[0100],而c[0100]只会直接影响[1000],而下表之间的关系恰好是也必须是k +=lowbit(k)。此时我们就是写出跟新维护树的代码:
void add(int k,int num)
{
while(k<=n)
{
tree[k]+=num;
k+=k&-k;
}
} 2. 数组区间求和
比如求0001~0110的和就直接c[0100]+c[0110],分析方法与上面的恰好逆过来,而且写法也是逆过来的,具体就不累述了:
int read(int k)//1~k的区间和
{
int sum=0;
while(k)
{
sum+=tree[k];
k-=k&-k;
}
return sum;
} 三、总结
首先,明白树状数组所白了是按照二分对数组进行分组;维护和查询都是O(lgn)的复杂度,复杂度取决于最坏的情况,也是O(lgn);lowbit这里只是一个技巧,关键在于明白c数组的构成规律;分析的过程二进制一定要深入人心,当作心目中的十进制。