BP神经网络:计算原理详解和MATLAB实现
声明:本文中图片资料和部分文字材料引自网络,仅为自己学习记录和供网络学习者分享,侵删。
目录
什么是人工神经网络(ANN)?
人工神经元模型
BP神经网络:
BP神经网络计算原理:
归一化
训练集、验证集、测试集,什么关系?
BP网络的MATLAB实践
参数对BP神经网络性能的影响:
【举例】对汽油辛烷值含量做预测:
神经网络现在已经用烂了,因此介绍部分我们只做简要介绍。如果对基础概念还不清楚的同学建议搜索网上其他一些学习资料先弄懂基本的一些概念。
什么是人工神经网络(ANN)?
来源于生物学概念:如维基百科中所言
In machine learning and cognitive science, artificial neural networks (ANNs) are a family of statistical learning models inspired by biological neural networks (the central nervous systems of animals, in particular the brain) and are used to estimate or approximate functions that can depend on a large number of inputs and are generally unknown.
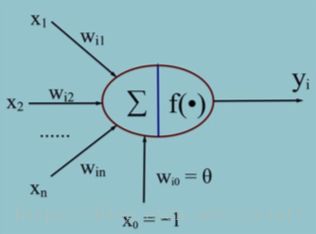
人工神经元模型
常用的激活函数:
神经网络的分类:
-
– 按照连接方式,可以分为:前向神经网络 vs. 反馈(递归)神经网络
-
– 按照学习方式,可以分为:有导师学习神经网络 vs. 无导师学习神经网络
-
– 按照实现功能,可以分为:拟合(回归)神经网络 vs. 分类神经网络
BP神经网络:
所谓BP只是神经学习训练的一个方法,是一种有监督的学习方法。BP的激活函数要求可微。
传播:
-
Forward propagation of a training pattern’s input through the neural network in order to generate the propagation’s output activations.
-
Back propagation of the propagation’s output activations through the neural network using the training pattern’s target in order to generate the deltas of all output and hidden neurons.
权重更新:
-
Multiply its output delta and input activation to get the gradient of the weight.
-
Bring the weight in the opposite direction of the gradient by subtracting a ration of it from the weight.
BP神经网络计算原理:
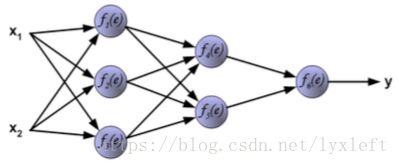
我们举一个4层的例子,如下图,有2个隐含层。
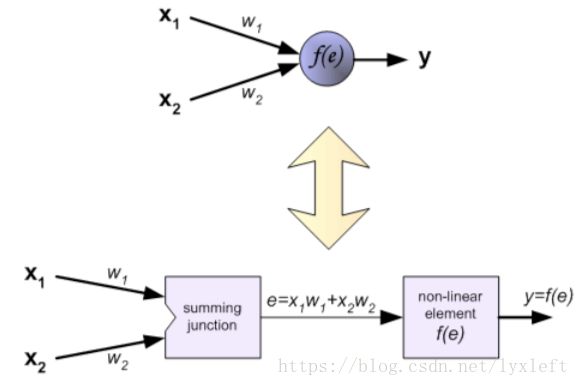
针对每一个神经元,它的计算方法是:
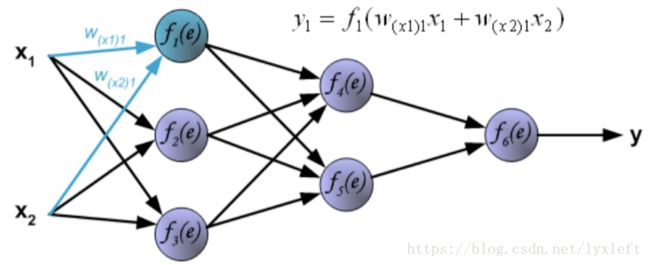
例如,第一个隐藏层的第一个神经元的计算结果是:
另外两个神经元,同理可得:
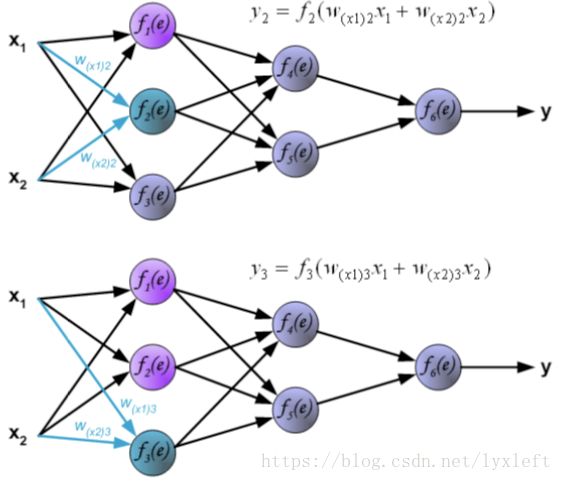
接下来,我们计算第二层隐含层:
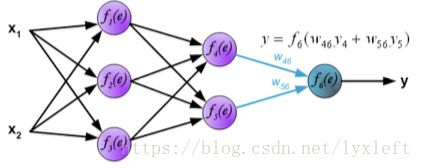
搞定之后,可以计算最后一层了:
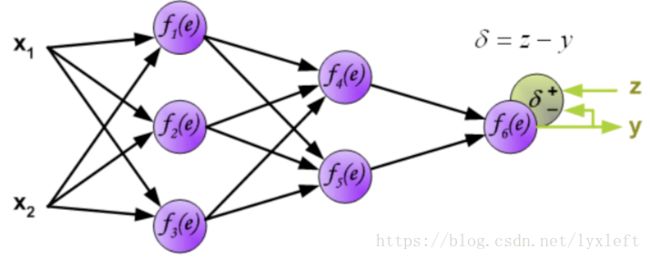
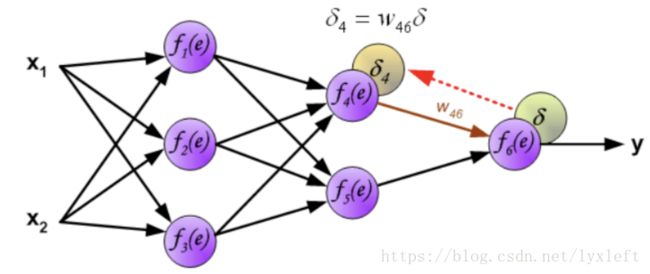
得到神经网络的输出y了,接下来就要做误差分析了。如,计算一个delta = z - y。这里只是一种简单的计算形式。一般我们还会使用误差平方和,如delta = 0.5(z-y)^2。
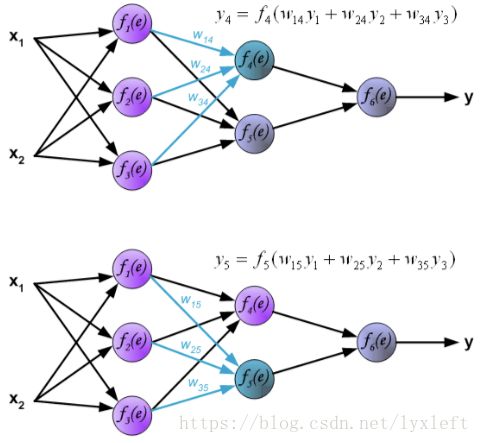
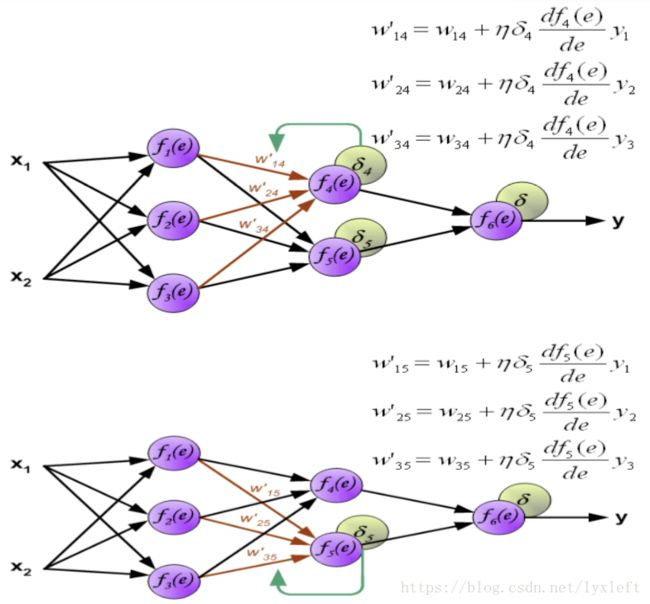
得到误差后,反向传播给前面的神经元,先乘上权重,得到某个神经元(如下图,f4)的误差:
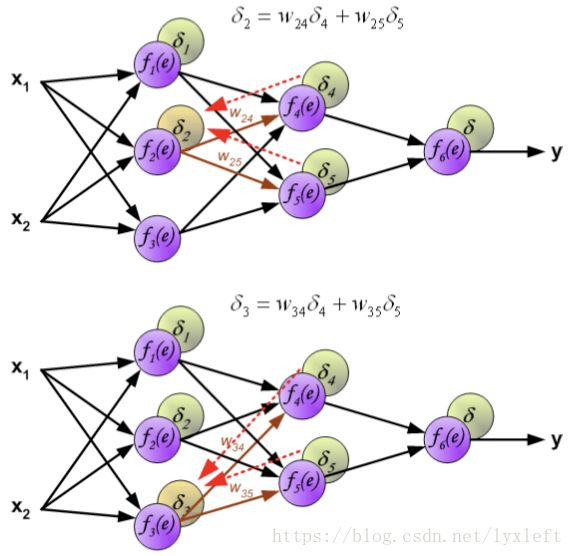
继续反向传播:
如此一直反向传播到第一层,这样就可以开始修正神经元之间的连接权重了。
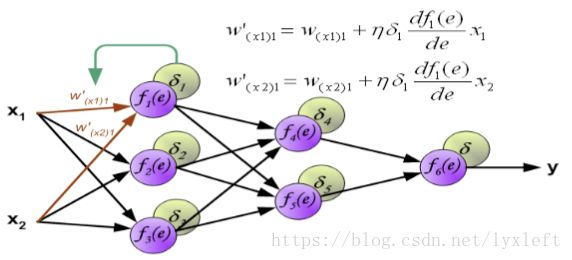
我们用到梯度下降法:原来的权重+一个误差项。
误差项中含义:yita 即学习率、delta 是反向传播回来的后面那一层的误差、激活函数求导形成的微分项。
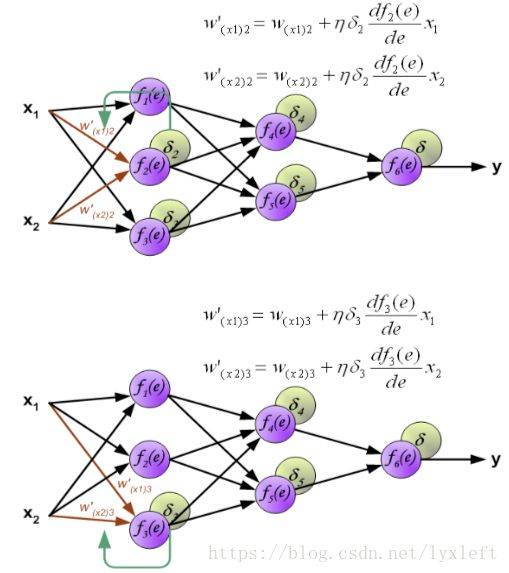
下面是分别修正f2和f3神经元的权值:
同理,第二个隐含层的权值修正:
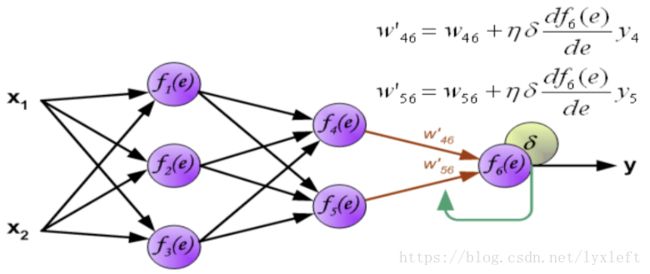
输出层:
如此一来就完成了一遍每一层连接权值的修正。
接下来就可以进行下一轮的循环:利用修正完的模型,再输入一个样本,正向传播等到y,再求delta,再反向传播回来逐层修复权值。如此循环反复就是BP神经网络的计算原理了。
归一化
什么是归一化?
——将数据映射到[0, 1]或[-1, 1]区间或其他的区间。
为什么要归一化?
-
– 输入数据的单位不一样,有些数据的范围可能特别大,导致的结果是神经网络收敛慢、训练时间长。
-
– 数据范围大的输入在模式分类中的作用可能会偏大,而数据范围小的输入作用就可能会偏小。(防止数据湮灭等现象)
-
– 由于神经网络输出层的激活函数的值域是有限制的,因此需要将网络训练的目标数据映射到激活函数的值域。例如神经网络的输出层若采用S形激活 函数,由于S形函数的值域限制在(0,1),也就是说神经网络的输出只能限制在(0,1),所以训练数据的输出就要归一化到[0,1]区间。
-
– S形激活函数在(0,1)区间以外区域很平缓,区分度太小。例如S形函数f(X)在参数a=1时,f(100)与f(5)只相差0.0067。这样数据的差异就会失去意义!
归一化的算法:
-
y = ( x - min )/( max - min ) —— 【0,1】
-
– y = 2 * ( x - min ) / ( max - min ) - 1 —— 【-1,1】
训练集、验证集、测试集,什么关系?
在有监督(supervise)的机器学习中,数据集常被分成2~3个,即:训练集(train set) 验证集(validation set) 测试集(test set)。
一般需要将样本分成独立的三部分训练集(train set),验证集(validation set)和测试集(test set)。其中训练集用来估计模型,验证集用来确定网络结构或者控制模型复杂程度的参数,而测试集则检验最终选择最优的模型的性能如何。一个典型的划分是训练集占总样本的50%,而其它各占25%,三部分都是从样本中随机抽取。
样本少的时候,上面的划分就不合适了。常用的是留少部分做测试集。然后对其余N个样本采用K折交叉验证法。就是将样本打乱,然后均匀分成K份,轮流选择其中K-1份训练,剩余的一份做验证,计算预测误差平方和,最后把K次的预测误差平方和再做平均作为选择最优模型结构的依据。特别的K取N,就是留一法(leave one out)。
BP网络的MATLAB实践
重点函数解读:
-
mapminmax
-
– Process matrices by mapping row minimum and maximum values to [-1 1]
-
– [Y, PS] = mapminmax(X, YMIN, YMAX) 归一化的信息保存到结构体PS中(自定义MIN,MAX范围)
-
– Y = mapminmax('apply', X, PS) 已知的归一化规则PS用于归一化其他信息
-
– X = mapminmax('reverse', Y, PS) 反归一化
-
-
newff
-
– Create feed-forward backpropagation network 创建前向型神经网络
-
– net = newff(P, T, [S1 S2...S(N-l)], {TF1 TF2...TFNl}, BTF, BLF, PF, IPF, OPF, DDF) 输入样本、输出样本、传递函数……等其他参数。
-
-
train
-
– Train neural network 训练神经网络
-
– [net, tr, Y, E, Pf, Af] = train(net, P, T, Pi, Ai)
-
-
sim
-
– Simulate neural network 模拟预测
-
– [Y, Pf, Af, E, perf] = sim(net, P, Pi, Ai, T) Y即最终预测的输出
-
参数对BP神经网络性能的影响:
1、隐含层神经元节点个数 ?
可以手动调整为其他个数,查看预测结果。
2、激活函数类型的选择 ?
newff里会默认设计好(tansig,双S型),还可以是其他函数。
3、学习率?——参考网络资料。
4、初始权值与阈值:
今后可以利用遗传算法对权值和阈值进行优化。
手动操作推荐方法:
1、交叉验证(cross validation):训练集(training set)+验证集(validation set)+测试集(testing set)。保证足够的样本,可以分到这三波里。
2、留一法(Leave one out, LOO):如果样本数据较少时使用。每一次都留一个样本做预测,其他用于训练。
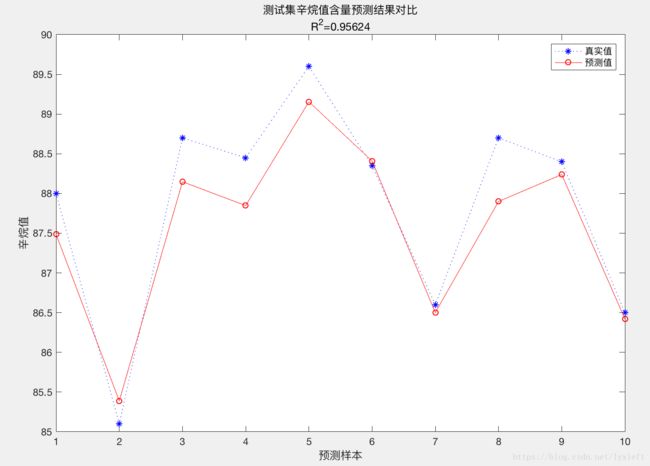
【举例】对汽油辛烷值含量做预测:
预测结果:
matlab代码:
%% I. 清空环境变量
clear all
clc
%% II. 训练集/测试集产生
%%
% 1. 导入数据
load spectra_data.mat
%%
% 2. 随机产生训练集和测试集
temp = randperm(size(NIR,1));
% 训练集――50个样本
P_train = NIR(temp(1:50),:)';
T_train = octane(temp(1:50),:)';
% 测试集――10个样本
P_test = NIR(temp(51:end),:)';
T_test = octane(temp(51:end),:)';
N = size(P_test,2);
%% III. 数据归一化
[p_train, ps_input] = mapminmax(P_train,0,1);
p_test = mapminmax('apply',P_test,ps_input);
[t_train, ps_output] = mapminmax(T_train,0,1);
%% IV. BP神经网络创建、训练及仿真测试
%%
% 1. 创建网络
net = newff(p_train,t_train,9);
%%
% 2. 设置训练参数
net.trainParam.epochs = 1000;
net.trainParam.goal = 1e-3;
net.trainParam.lr = 0.01;
%%
% 3. 训练网络
net = train(net,p_train,t_train);
%%
% 4. 仿真测试
t_sim = sim(net,p_test);
%%
% 5. 数据反归一化
T_sim = mapminmax('reverse',t_sim,ps_output);
%% V. 性能评价
%%
% 1. 相对误差error
error = abs(T_sim - T_test)./T_test;
%%
% 2. 决定系数R^2
R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2));
%%
% 3. 结果对比
result = [T_test' T_sim' error']
%% VI. 绘图
figure
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值')
xlabel('预测样本')
ylabel('辛烷值')
string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};
title(string)
参考资料:
1、[综] 训练集(train set) 验证集(validation set) 测试集(test set)
http://www.cnblogs.com/xfzhang/archive/2013/05/24/3096412.html
2、matlab_geeker,http://edu.dataguru.cn
3、维基百科