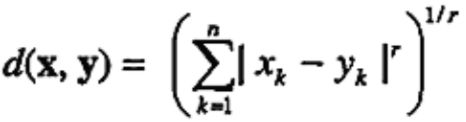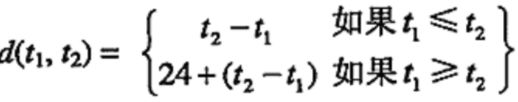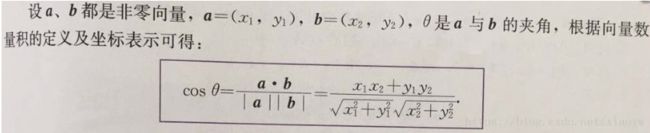数据的相似性和相异性的度量

要讨论相似度（similarity）和相异度（dissimilarity），我们先引入一个术语叫邻近度（proximity）。邻近度可以表示相似性或者相异性，相当于是一个总括概念。邻近度度量有很多，比如相关和欧几里得距离（在时间序列这样的稠密数据或者二维点用到）、余弦相似度和Jaccard系数（文档类稀疏数据）。我们接下来简明扼要地来探讨梳理一下。

本文讲解的目录是：

一、相异度

二、相似度

三、邻近性度量实例

四、邻近度计算问题

五、如何选择邻近性度量

---

一、相异度

距离

我们最属性的距离就是欧几里得距离d。这是我们中学时就用到的。引申到一维、二维、或更高维度的数据空间中也一样适用。它就是表征两个数据（点）之间的差距嘛！所以可以用来表征相异度。

如果一个点有多个属性值，如x={x1,x2...xk}, y={y1,y2...yk}，那么他们的欧几里得距离可以表示为：

但是我们到了大学之后，特别是研究生搞科研阶段，不好意思再用这么简单的距离了吧？应该说是要根据问题的形态选取合适的度量（这个我们在本文第5部分深入讲）。所以有些牛人就构造了更牛x的距离表达式，瞬间让你高大上的：

闵可夫斯基距离：

r=1：城市街区距离。比如常见的汉明距离。实际上是表征两个二元向量之间不同的二进制位的个数。二元向量就是具有二元属性的对象，在上一篇博文《数据预处理工作中的几个关键主题探讨：聚集、抽样、降维、变量变换等》中我们讲过如何用二元属性来表征一个数据对象哦！

r=2：欧几里得距离。就是我们上面讲的。也叫L2范数。范数是矩阵论中的内容，若有兴趣可以自学了解一下！也是很有用的。

r=∞：上确界距离。也叫无穷范数。是对象属性之间的最大距离。即表示为：

需要指出的是，距离具有一些通用的性质。

1、非负性。距离肯定是非负数的。

2、对称性。d(x,y)=d(y,x)。

3、三角不等式。即两边之和大于（这里可以等于）第三边！！d(x,z)≤d(x,y)+d(y,z)。

满足这些性质的测度才可以称为度量。但是实践中根据需要我们常常违反这一规定。比如：时间。

比如d(1pm,2pm)=1h，而d(2pm,1pm)=23h，这种定义是有意义的，考虑到了隔天（跨天）的实际情况。但是不符合上面的度量的全部性质。

二、相似度

对于相似度，三角不等式通常不成立，但对称性和非负性通常成立。

用s(x,y)表示相似度。则：

1、s取值范围是[0,1]，当且仅当x=y时s=1。

2、s(x,y)=s(y,x)。即对称性。

三、邻近性度量实例

这里我们讨论几种邻近性度量实例，包括二元数据的度量、余弦相似度、非常重要的统计学概念相关性等等。

二元数据的相似性度量——相似系数（similarity coefficient）

设x,y是两个二元向量。记：

f00=x取0且y取0的属性个数；

f01=x取0且y取1的属性个数；

f10=x取1且y取0的属性个数；

f11=x取1且y取1的属性个数。

简单匹配系数（Simple Matching Coefficeient, SMC）

注意到，SMC对属性为0的也进行了技术。而更多时候我们不关心属性记号为0，我们只关心一个对象有什么属性，而不是他不具有什么属性。所以SMC可能更适合0和1标号同等重要的情况，比如判断对错的是非题。

Jaccard系数

对上述问题做了改进：

我们通过一个例子比较二者：

余弦相似度

余弦相似度常使用在文档数据中。它可以忽略0-0的匹配，而且还能够处理非二元的向量。

这个计算就是中学时候求向量夹角一样简单：

只是这里x，y可能是高维的向量，因为机器学习、数据挖掘中，数据的维度都比较高。求法是把对应位置坐标（属性值）相乘后求和、除以模长乘积就可以了。或者先对每个向量做标准化（归一化），然后坐标相乘求和。

有时候判断两个数据是否属于同一类，就用余弦相似度来评价。

广义Jaccard系数

也可以用于文档数据，只是在二元属性情况下则规约为Jaccard系数（上面讲到了）。

该系数用EJ表示：

这样比简单的Jaccard系数扩展了一些，可以适用于非二元属性的简单数据对象情形之中了。

相关性

即皮尔森相关系数：是统计学中非常重要的概念，在数据处理领域也常常用得上。

其中：

相关系数值域[-1,1]，1表示完全正相关，-1表示完全负相关。若为0表示两个对象之间不具备线性关系（但可能存在非线性关系）。

需要注意的是，皮尔逊系数只是表达是否具有线性关系！不能完全依赖它作为数据相似性的度量。

四、邻近度计算中几个重要问题

1、当属性具有不同值域？

标准化！都归为[0,1]！

2、当属性具有不同类型？

简单粗暴，把异种属性忽略掉！

3、当属性权重不同？

修改邻近度公式，对每个属性的贡献加权，一般情况下，wk和为1。则上面（2-15）改写为：

闵可夫斯基距离改写为：

4、属性之间相关？

用Mahalanobis距离！

其中，Σ是协方差矩阵。它的第ij个元素是第i个和第j个属性的协方差。

五、如何选择邻近性度量

一言以蔽之，所选择的邻近性度量要与数据类型相对应。比如连续稠密的数据，常常用距离来描述。对于上面讲到的，需要忽略0-0匹配的数据，就可以用余弦相似度或者Jaccard系数。广义的Jaccard系数不仅仅只适用于具备二元属性的对象。等等。

最好是我们在处理这堆数据前先查资料看看前人使用何种度量。如果别人已经论证过哪种度量在哪种算法中好用，就引用他的论证就好了，站在巨人的肩膀上，高瞻远瞩！

感谢您的阅读和对原创分享的支持。