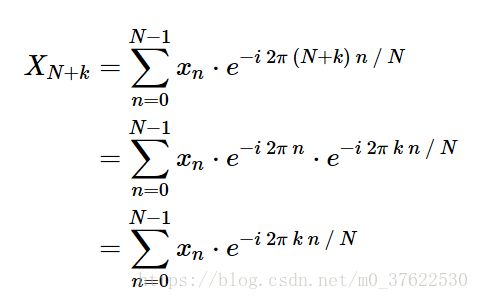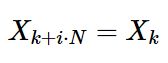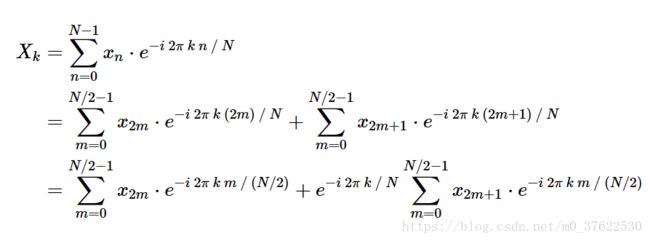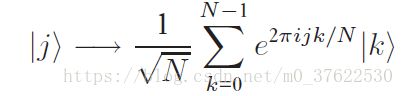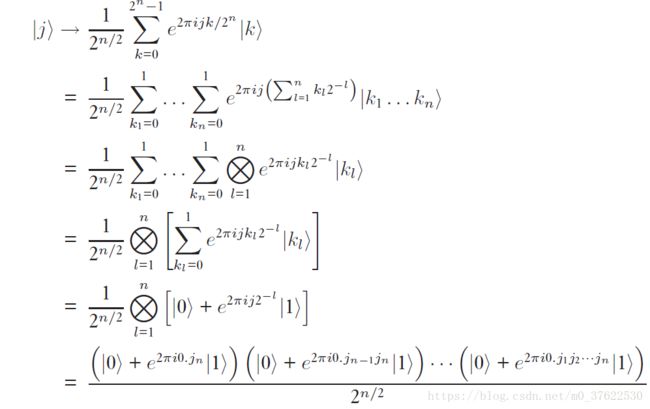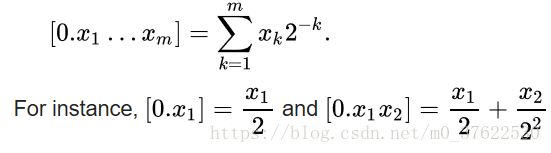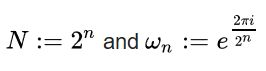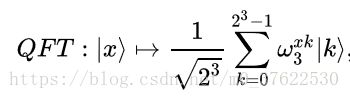快速傅里叶变换(FFT)和量子傅里叶变换(QFT)

这篇文章主要是为了实现量子傅里叶变换(Quantum Fourier Transform, QFT)的programming做准备，对QFT的算法以及它和在传统计算机上运行的FFT进行比较。

目录

1 FFT

1.1 DFT与FFT

1.2 FFT原理

1.3 FFT算法实现

2 QFT

2.1 QFT原理

2.1.1 计算推倒

2.1.2 量子电路

2.1.3 QFT幺正矩阵/量子门

2.2 举例

2.3 QFT和FFT对比

3 代码部分

参考文献与推荐阅读

---

1 FFT

FFT快速傅里叶变换是一种快速计算离散傅里叶变换(DFT)以及其逆变换(IDFT)的方法。简单起见，这里我们只对其正变换进行讨论。

1.1 DFT与FFT

	DFT	FFT
定义式
时间复杂度

1.2 FFT原理

FFT能够大幅度对传统的DFT提速的原因在于，利用了傅里叶变换的对称性。

根据上面表格里的DFT定义式，用N+k代替k，我们不难得到:

这说明Xk是每N个loop后一重复的，即:

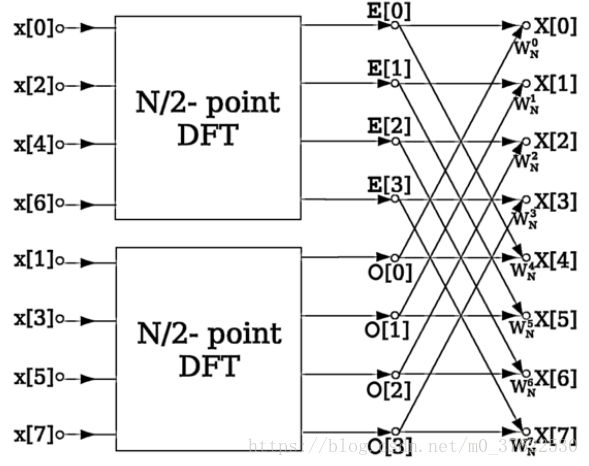
利用这种对称性，Cooley-turkey算法证明了，我们可以将DFT分为两部分，如下:

同理，上图中的拆分可以继续进行下去(代码体现为一个递归函数)，因此我们不难发现最终的算法复杂度降低为了。

1.3 FFT算法实现

2 QFT

2.1 QFT原理

Quantum Fourier transform是传统的离散傅里叶变换(DFT)的量子解决办法。

DFT的计算式为:

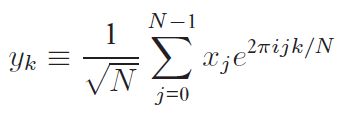，其中x_0,...,x_{N-1}是一个由复数组成的向量。

量子计算做的就是首先计算量子态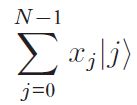，然后再将它映射到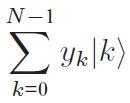去，其中yk就是DFT定义式的所求。

这样的映射也等同于:

2.1.1 计算推倒

（感谢sky-edge的更正，上图中的j_l j_{l+1}...j_m应该是0.j_l j_{l+1}...j_m。）

由此可以对之前的QFT映射做出以下变换:

其中推导过程中出现的表示的是n项相乘。而0.j1j2...jn的表示就是我们刚刚讨论的二进制:

2.1.2 量子电路

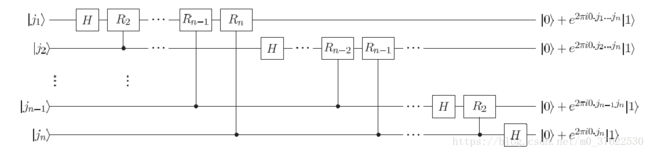
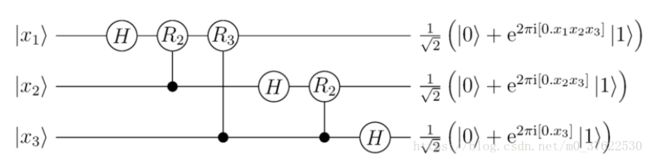
由这样的结果，我们可以将量子傅里叶变换表示为一个量子电路(Quantum Circuit):

其中H是Hadamard门，Rk表示的是幺正矩阵形式为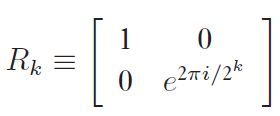的量子门。具体这些门的计算可以在参考文献3或4中详细阅读，最终得到的qubits state是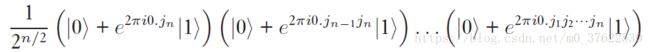，和2.1.1保持一致。

对于第一个qubit我们用了1个H门和n-1个Rk门(conditional rotations)，对于第二个qubit我们用了1个H门和n-2个Rk门(conditional rotations)...所以总共用的门的数量是n+(n-1)+(n-2)+...+1=n(n+1)/2个。上图中省略了一些SWAP运算(用来在计算后交换qubits的位置，应该第一行与最后一行交换，第二行与倒数第二行交换...全部换完后，和2.1.1中的最终算式的顺序保持一致)，最多有n/2个SWAP运算，每个SWAP可以用3个CNOT门实现。因此QFT所用的门的数量是O(n^2)。

对于FFT来说，门的数量是O(n·2^n)。

2.1.3 QFT幺正矩阵/量子门

量子傅里叶变换也可以用一个幺正矩阵&量子门表示(任意一种量子门都是幺正矩阵，反之，任意幺正矩阵也是量子门):

, 其中

2.2 举例

此处我们以3qubits的QFT为例进行阐述。

，矩阵表示为:

量子电路为:

经过这个量子电路后，再使用1个SWAP门将第1个和第3个qubit进行交换，就可以得到公式:

我们现在可以假设输入的三个qubit |x1>, |x2>, |x3>都是|0>，计算一下最终的结果:

 

因此最终{000, 001, 010, 011, 100, 101, 110, 111}这八种情况出现的概率是一样的。

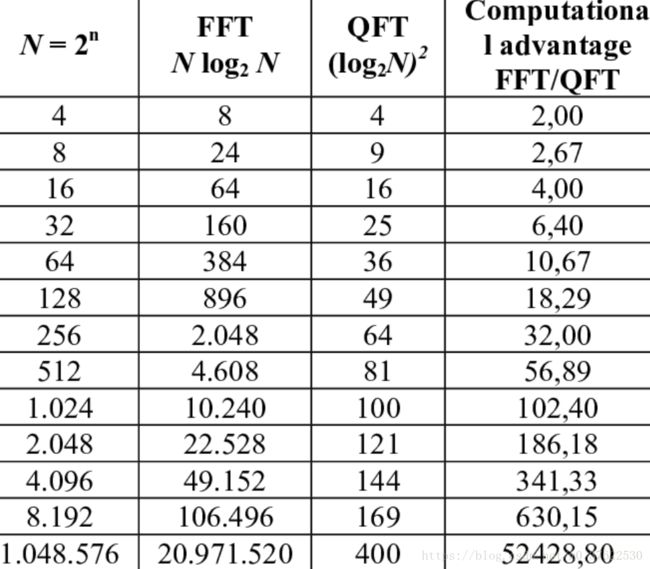
2.3 QFT和FFT对比

速度对比为:

computational cost和二者使用的门的数量是直接挂钩的。如果我们把N和n的关系带入这两个computational cost，就会发现结果和本文的2.1.2部分结论一致。

3 代码部分

参见我的 github 或者这篇CSDN文章(IBM QISKit+Python3.6+Jupyter Notebook实现)。

参考文献与推荐阅读

1. FFT中文维基百科

2. Understanding the FFT Algorithm

3. DFT英文维基百科

4. 教材 Quantum Computation and Quantum Information ，Neilson，P217

5. 文章Quantum Machine Learning for Data Scientists，P23

5. 论文 Quantum Circuit Proposal to Solar Visualization using BDA Radiointerferometer