Faster RCNN中RPN理解（需要训练得到粗略proposals的）、附画图代码。biu~

fast+rpn=faster rcnn

之前已经用过RPN，因为重心一直在修改我自己的网络结构上，这次重新涉及到此部分的优化（Guided Anchoring: 物体检测器也能自己学 Anchor），重新审视了一下RPN，记录一下。

如果把RPN看作一个黑盒子的话，最关心的问题是，输入和输出。RPN输入的是一张图片，输出输出一系列的矩形object proposals。RPN其实就像个“内嵌的”的网络似的，这也正是“两阶段物体检测”的体现之处，进行了初步、首阶段的学习。

（RPN相当于是一个小的、粗糙的目标检测cnn模型，只不过它不具体识别/分类，它的识别/分类是：是前景还是背景；定位是：根据anchor使得检测的框靠近gt_box（回归：做怎样的逼近才能使得anchor逼近gt-boxes）。这时候结果不是很准确，只能大致确定框的位置，后面fast rcnn会进一步精确。这个RPN实际上就是一个attention机制，这也是两阶段法比一阶段法（YOLO等）准确的原因）

训练步骤：

1.将图片输入到VGG或resnet等的可共享的卷积层中，得到最后可共享的卷积层特征图FM（feature map）。

2.将FM送入RPN。（先3*3filter滑窗生成新的FM（intermediate layer），再送入两个1*1conv）

    2.1在滑动窗口的每个像素点根据感受野都对应的原图上的一片区域，这片区域对目标的覆盖力、形状多样性可能没有那么好，故根据此区域的中心点（锚点），在原图设置9/15个矩形窗口（eg：3种长宽比*3种尺度），即锚框、anchor。至于这里为什么要在原图上，是因为最后求出来的锚框要跟原图的标定框最小梯度下降。

   2.2将卷积的结果和锚点分别输入到两个小的1*1的网络中reg（回归，求目标框的位置）和cls（分类，确定该框中是不是目标）

3.训练集标记好了每个框的位置，和reg输出的框的位置比较，用梯度下降来训练网络。

4.得到的proposals将会根据strides被部署在一幅尺寸为w×h的特征图上（映射），注意这个时候映射出的是一块区域了，因为原来是的根据感受野中心点扩的9个框，回归后某个、某几个框映射过去是一个区域。比如：

# anchors 尺寸  3种尺寸大小，3种比例。故一个锚点生成9个anchors
scales = [2,4,8]#根据这个生成9种尺寸，但面积都为4,16,64
# scales = [32,64,128,256,512]
ratios = [0.5, 1.0, 2.0]

注意：anchors是在原图上的。在FM上对点做信息抽取时候，相当于抽取该点在原图上对应的一堆anchors的信息（分类和回归信息）。FM一个点对应原图的感受野，围绕感受野中心做的一堆anchors的信息。也就是说特征图中的每个位置都与具有预定义的尺度和纵横比的k个anchors相关联。

图片节选自https://www.bilibili.com/video/av21846607/?p=6（视频不建议看，建议看这个系列：https://www.bilibili.com/video/av29987414）

ROI Pooling : anchor 到FM上的ROI进行pooling

Region Proposal Networks（RPN）

（RPN是faster-Rcnn的一部分，faster-Rcnn论文原文自行找）

RPN网络把一个任意尺度的图片作为输入，输出一系列的矩形object proposals，每个object proposals都带一个objectness score。用一个全卷积网络来模拟这个过程，这一小节描述它。因为最终目标是与Fast R-CNN目标检测网络来共享计算，所以假设两个网有一系列相同的卷积层。研究了the Zeiler and Fergus model（ZF），它有5个可共享的卷积层，以及the Simonyan and Zisserman model（VGG-16），它有13个可共享的卷积层。

为了生成region proposals，在卷积的feature map上滑动一个小的网络，这个feature map 是特征提取层最后一个共享卷积层的输出。这个小网络需要输入卷积feature map的一个n*n窗口。每个滑动窗口都映射到一个低维特征（resnet+fpn中是256维，VGG是512维，后面跟一个ReLU激活函数）。这个特征被输入到两个并列全连接层中（一个box-regression层（reg），一个box-classification层（cls））。在这篇论文中使用了n=3，使输入图像上有效的接受域很大（ZF 171个像素，VGG 228个像素）。这个迷你网络在图3（左）的位置上进行了说明。注意，由于迷你网络以滑动窗口的方式运行，所以全连接层在所有空间位置共享。这个体系结构是用一个n*n的卷积层来实现的，后面是两个1*1的并列卷积层（分别是reg和cls）。

要保证下面三个layer的尺寸一致性（空间位置一致，有助于后面直接找到anchor），也就是：

假设：FM尺寸W,H,C，则intermediate layer：经过3*3*C→W,H,1,然后cls layer经过1*1*2k→W,H,2k；reg layer经过1*1*4k→W,H,4K。如图：

 

1.1Anchors（锚点）

在每个滑动窗口位置，同时预测多个region proposals，其中每个位置的最大可能建议的数量表示为k。所以reg层有4 k输出来编码k个box的坐标（可能是一个角的坐标（x，y）+width+height），cls层输出2 k的分数来估计每个proposal是object的概率或者不是的概率。这k个proposals是k个参考框的参数化，把这些proposals叫做Anchors（锚点）。锚点位于问题的滑动窗口中，并与比例和纵横比相关联。默认情况下，使用3个尺度和3个纵横比，在每个滑动位置上产生k=9个锚点。对于W *H大小的卷积特性图（通常为2,400），总共有W*H*k个锚点。

平移不变性的锚点

RPN的一个重要特性是是平移不变性，锚点本身和计算锚点的函数都是平移不变的。如果在图像中平移一个目标，那么proposal也会跟着平移，这时，同一个函数需要能够在任何位置都预测到这个proposal。我们的方法可以保证这种平移不变性。作为比较，the MultiBox method使用k聚类方法生成800个锚点，这不是平移不变的。因此，MultiBox并不保证当一个对象被平移式，会生成相同的proposal。

平移不变性也减少了模型的尺寸，当锚点数k=9时，因为MultiBox锚点不具有平移不变性，所有它要求一个(4+1)×800维的全连接输出层，而这篇论文的方法有一个（4+2）*9维的卷积输出层。因此，输出层的参数比MultiBox少两个数量级（原文有具体的数，感觉用处不大，没有具体翻译）。如果考虑到feature projection层，建议层仍然比MultiBox的参数少了一个数量级。这里的建议层有一个数量级的参数减少（使用GoogLeNet 的MultiBox有27百万，而使用VGG-16的RPN有2.4百万），因此在想PASCAL VOC这样的小数据集上有更少过拟合的风险。

多尺度锚点作为回归参考

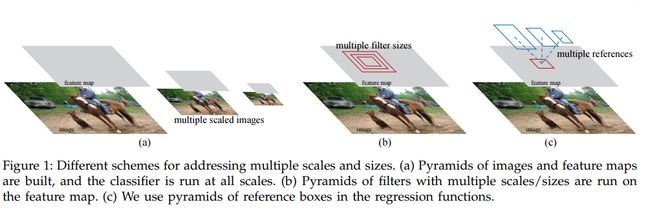
  锚点设计提出了一种解决多个尺度（和纵横比）的新方案。如图所示，有两种流行的多尺度预测方法。

（a．建立了图像和特征图的金字塔，分类器在所有的尺度上运行。b. 具有多个尺寸/大小的过滤器金字塔在feature map上运行。c. 我们在回归函数中使用了参考框的金字塔。）

第一种方法是基于图像/特征金字塔，例如，在DPM和基于cnn方法的方法。这些图像在多个尺度上进行了调整，并且为每个尺度计算特征图（占用或深度卷积特性）（图1（a））。这种方法通常很有用，但很耗费时间。第二种方法是在feature map上使用多个尺度（和/或方面比率）的滑动窗口。例如，在DPM中，不同方面比率的模型分别使用不同的过滤大小（如5 7和7 5）进行单独训练。如果这种方法用于处理多个尺度，它可以被认为是一个过滤器金字塔（图1（b））。第二种方法通常是与第一种方法共同使用的

相比而言，基于锚点的方法建立在锚点金字塔上，这更节省成本。RPN对多个尺度和纵横比的锚点框进行了分类和回归。它只依赖于单一尺度的图像和feature map，并使用单一大小的过滤器（feature map上的滑动窗口）。实验展示了这个方案对处理多个尺度和大小的影响（表8）。

由于这种多尺度设计是基于锚点的，可以简单地使用在单尺度图像上计算的卷积特性，也可以使用Fast R-CNN检测器。多尺度锚点的设计是共享特性的关键组成，使处理尺度时不需要额外的成本。

1.2损失函数

为了训练RPNs，（既然训练就要样本，小网络已经有了，那么接下来）

（1）样本制作：

将一个二进制类标签（是否是object）分配给每个锚点。会给这两种锚点设置成正标签：1）跟真值框的交并比最高的。2）跟真值框的交并比大于0.7的。因此，一个真值框可以对应多个正标签的锚点。通常第二个条件足以确定正样本，我们还用第一种情况的原因是，有的时候第二种情况找不到正样本。如果一个锚点跟所有真值框的交并比小于0.3，那马我们就把它设为负样本。正负样本之间的这些样本对训练没有贡献。

（2）损失函数：

在fast R-CNN的多任务损失之后最小化一个目标函数，一张图片的损失函数定义为：

i 是每个小批量中锚点的序号，p是锚点i是目标的概率，p*是标签（只能是0或1），t是预测框的4个参数，t*是标定框的参数；是分类损失函数，是回归损失函数；表示回归只对正样本进行（负样本=0）。cls和reg分别输出和。

这两部分由（小批量的大小决定，这里是~2000个proposals，只选256个进行训练）和Nreg（锚点位置数量决定，这里是2400）进行规范化，并通过一个平衡参数λ进行加权。默认情况下，设置λ=10，因此cls和reg部分的权重大致相同。作者通过实验证明，结果对在大范围内λ的值不敏感。作者还注意到，上面的标准化是不需要的，可以被简化。λ=9.375完全相同。

对于边界框回归，采用了以下4个坐标的参数化：

 x，y，w，h表示框的中心坐标以及它的宽度和高度。变量x、和x*分别代表预测的框、锚点框和真值框（y、w、h类似）。这可以认为是锚点框向附近真值框回归。是一种微调的感觉。

用与以前基于ROI（感兴趣的区域）方法不同的方法实现了有界的回归。原来的方法在从任意大小的RoIs中集合的特性上执行有界的回归，并且所有区域大小都共享回归权重。在作者的公式中，用于回归的特性在feature maps上具有相同的空间大小（3*3）。为了计算不同的尺寸，学习了一组k个有界的回归。每一个回归器负责一个尺度和一个纵横比，而k个回归器不共享权重。因此，由于锚点的设计，仍然可以预测各种大小的框，即使这些特征是固定的大小/比例。

1.3 训练RPNs

RPN可以通过反向传播和随机梯度下降来端到端训练。遵循以图像为中心的采样策略，开始训练这个网络。每个小批次都来自同一张照片，照片包含许多正负锚点示例。对所有锚点的损失函数进行优化是可行的，但这将偏向于负样本，因为它们多。相反，在一个图像中随机抽取256个锚点来计算一个小批的损失函数，其中采样的正和负锚点的比例是1:1。如果一个图像中有少于128个正的样本，用负样本填充。

随机地初始化所有的新层，方法是用标准偏差0.01的零均值高斯分布来初始化权重。通常，所有其他层（共享卷积层）都是通过预先培训练一个用于ImageNet分类的模型来初始化的。对ZF网络的所有层进行调优，并对VGG网络的conv3_1层进行调优，以节省内存。对60 k小批量的学习速率为0.001，在PASCAL VOC数据集上的下一个20 k小批量的学习速率是0.0001。使用0.9的步长和0.0005的重量衰减。用Caffe实现的。

初步会根据概率筛选一部分，余下得分高、高度重叠的proposals，再用nms进行循环抑制。

参考：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches

# F_X,F_Y = np.meshgrid(f_x,f_y)
# print(F_X,'\n',F_Y)

# scales,ratios = np.meshgrid(scales,ratios)
# print(scales.flatten(),'\n',ratios.flatten())

def anchor_gen(size_x,size_y,rpn_stride,scales,ratios):
    ## 从坐标向量返回坐标矩阵，shape:(len(a),len(b))。 可以debug看下怎么排的
    # len:5,3 →shape: (3, 5)  (3, 5) 把scales的值按行排列（横着排），共len(ratios)行；ratios按列排列，共len(scales)列
    scales, ratios = np.meshgrid(scales, ratios)
    scales, ratios = scales.flatten(),ratios.flatten()#len(scales)*len(ratios)；len(ratios)*len(scales)
    # 根据尺寸、比例生成的anchors框的尺寸。sqrt是因为这里是算边的。scales是面积
    scalesX = scales / np.sqrt(ratios)
    scalesY = scales * np.sqrt(ratios)
    print(scalesX.shape,'\n',scalesY.shape)# 用他俩对应位置组合就能组合出anchors
    # 映射到原图的坐标点即锚点，再组合
    shiftX = np.arange(0,size_x) * rpn_stride
    shiftY = np.arange(0,size_y) * rpn_stride
    print('shiftX,shiftY',shiftX.shape,shiftY.shape)  # (40,) (24,)
    # 锚点们 anchors
    shiftX,shiftY = np.meshgrid(shiftX,shiftY)        #
    print('shiftX,shiftY',shiftX.shape,shiftY.shape)  #(24, 40) (24, 40)
    # 锚点+尺寸+比例 生成的anchors
    centerX,anchorX = np.meshgrid(shiftX,scalesX)# (24, 40)；15
    centerY,anchorY = np.meshgrid(shiftY,scalesY)# : (15, 960)
    print('centerX.shape:',centerX.shape,'centerY.shape:',centerY.shape,"total num of anchors:",centerX.shape[0]*centerX.shape[1]) #(16, 16)
    # 中心点和尺寸融合
    anchor_center = np.stack([centerY,centerX],axis=2).reshape(-1,2)
    anchor_size = np.stack([anchorY,anchorX],axis=2).reshape(-1,2)
    # 左上顶点、右上顶点
    boxes = np.concatenate([anchor_center-0.5*anchor_size,anchor_center+0.5*anchor_size],axis=1)
    return boxes


if __name__ == "__main__":
    img = np.ones((128,128,3))

    #共享FM的尺寸，影响anchors总个数。scales和ratios影响FM上一个点代表的anchors个数
    size_x = 16
    size_y = 16
    # 缩放倍数 8
    rpn_stride = img.shape[0]//size_x  #/mask第四层是32，(1333, 800)。image_size = 16 * 8
    # anchors 尺寸  5种尺寸大小，3种比例。故一个锚点生成15个anchors
    #根据这个生成9种尺寸，但面积为16,64,128...
    scales = [4, 8, 16, 32,64]
    ratios = [0.5, 1.0, 2.0]

    f_x = np.arange(size_x) * rpn_stride
    f_y = np.arange(size_y) * rpn_stride
    anchors = anchor_gen(size_x,size_y,rpn_stride,scales,ratios)#: (14400, 4)
    plt.figure(figsize=(10,10))
    plt.imshow(img)
    Axs = plt.gca()# get current axs得到当前的接口
    for i in range(anchors.shape[0]):
        box = anchors[i]
        rec = patches.Rectangle((box[0],box[1]),box[2]-box[0],box[3]-box[1],edgecolor='r',facecolor="none")
        Axs.add_patch(rec)
    plt.show()

 

https://www.cnblogs.com/jiangnanyanyuchen/p/9433791.html

https://www.cnblogs.com/hellcat/p/9811301.html