RNN学习笔记

1. RNN概述

CNN网络被用于处理图像数据，而对于非连续的数据处理一般是采用RNN网络进行实现的。对于经典的RNN网络其基本结构组成如下图所示

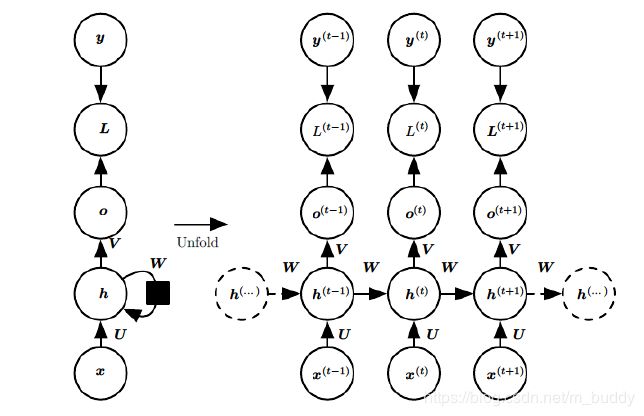
上图中左边是RNN模型没有按时间展开的图，如果按时间序列展开，则是上图中的右边部分。我们重点观察右边部分的图。这幅图描述了在序列索引号$t$附近RNN的模型。其中：

1. $x^{(t)}$代表在序列索引号$t$时训练样本的输入。同样的，$x^{(t-1)}$和$x^{(t+1)}$代表在序列索引号$x^{(t-1)}$和$x^{(t+1)}$时训练样本的输入。
2. $h^{(t)}$代表在序列索引号$t$时模型的隐藏状态。$h^{(t)}$由$x^{(t)}$和$h^{(t-1)}$共同决定。
   3）$o^{(t)}$代表在序列索引号$t$时模型的输出。$o^{(t)}$只由模型当前的隐藏状态$h^{(t)}$决定。
3. $L^{(t)}$代表在序列索引号$t$时模型的损失函数。
4. $y^{(t)}$代表在序列索引号$t$时训练样本序列的真实输出。
5. $U,W,V$这三个矩阵是我们的模型的线性关系参数，它在整个RNN网络中是共享的，这点和DNN很不相同。

2. RNN前向算法与后向算法

2.1 前向算法

在RNN中隐状态$h^{(t)}$的计算可以参考如下公式表示，最后简化后的形式同一般神经元相同，输入信息乘权重加偏值：
$$h^{(t)}=\sigma (U{x}^t+W{h}^{(t-1)}+b)$$
其中$\sigma$为RNN的激活函数，在隐层一般为$tanh$，这里补充一下：这里选择隐层的激活函数为$tanh$，但是由于连乘关系会存在梯度消失问题，自然可以采用Relu函数，但防止梯度爆炸，需要进行剪裁操作，对于这样的问题在LSTM变形中进行了改进。$b$为线性偏置。

在RNN中由于后序时刻对前序的输入是存在依赖关系的，但是梯度传递的时候是连乘的关系，这就导致了梯度问题，这是在知乎上找到的一个解释：

则输出$o^t$表示为：
$$o^{(t)}=V{h}^{(t)}+c$$

之后的分类输出是在这个的基础上经过softmax（输出层）映射得到，可以表示为
$$y^{(t)}=\sigma (o^{(t)})$$

最后$L^{(t)}$通过计算$\widehat{y^{(t)}}$与$y^{(t)}$之间的差异来更新网络

2.2 反向传播

有了RNN前向传播算法的基础，就容易推导出RNN反向传播算法的流程了。RNN反向传播算法的思路和DNN是一样的，即通过梯度下降法一轮轮地迭代，得到合适的RNN模型参数$U,W,V,b,c$。由于我们是基于时间反向传播，所以RNN的反向传播有时也叫做BPTT(back-propagation through time)。当然这里的BPTT和DNN也有很大的不同点，即这里所有的$U,W,V,b,c$在序列的各个位置是共享的，反向传播时我们更新的是相同的参数。

为了简化描述，这里的损失函数我们为对数损失函数，输出的激活函数为$softmax$函数，隐藏层的激活函数为$tanh$函数。对于RNN，由于我们在序列的每个位置都有损失函数，因此最终的损失L为：
$$L=\sum _{t=1}^T{L}^{(t)}$$
其中$V,c$的梯度计算式比较简单的：
$$\frac{\partial L}{\partial c}=\sum _{t=1}^T\frac{\partial L^{(t)}}{c}=\sum _{t=1}^T\frac{\partial L^{(t)}}{o^{(t)}}\frac{\partial o^{(t)}}{c}=\sum _{t=1}^T\widehat{y^t}-y^{(t)}$$
$$\frac{\partial L}{\partial V}=\sum _{(t=1)}^T\frac{\partial L^{(t)}}{\partial V}=\sum _{t=1}^T\frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial V}=\sum _{t=1}^T(\widehat{y^t}-y^{(t)})(h^{(t)}{)}^T$$

但是$W,U,b$的梯度计算就比较的复杂了。从RNN的模型可以看出，在反向传播时，在某一序列位置$t$的梯度损失由当前位置的输出对应的梯度损失和序列索引位置$t+1$时的梯度损失两部分共同决定。对于$W$在某一序列位置$t$的梯度损失需要反向传播一步步地计算。我们定义序列索引$t$位置的隐藏状态的梯度为：
$${\delta }^{(t)}=\frac{\partial L}{\partial h^{(t)}}$$
这样我们可以像DNN一样从${\delta }^{(t+1)}$递推${\delta }^{(t)}$
$${\delta }^{(t)}=\frac{\partial L}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}+\frac{\partial L}{\partial h^{(t+1)}}\frac{\partial h^{(t+1)}}{\partial h^{(t)}}=V^T(\widehat{y^{(t)}}-y^{(t)})+W^T{\delta }^{(t+1)}diag(1-(h^{(t+1)}{)}^2)$$
对于${\delta }^{(T)}$，由于它是最后一个了，因而后面的那一部分就没有了，所以
$${\delta }^{(T)}=\frac{\partial L}{\partial o^{(T)}}\frac{\partial o^{(T)}}{\partial h^{(T)}}=V^T(\widehat{y^{(t)}}-y^{(t)})$$
这样前面$T-1$时刻加上$T$传递给的梯度，这样就可以实现梯度传递了。继而，有了${\delta }^{(t)}$，计算$W,U,b$就容易了，这给出它们的计算表达式：
$$\frac{\partial L}{\partial W}=\sum _{t=1}^T\frac{\partial L}{\partial h^{(t)}}\frac{\partial h^{(t)}}{\partial W}=\sum _{t=1}^{T}diag(1-(h^{(t)}{)}^2){\delta }^{(t)}(h^{(t)}{)}^T$$
$$\frac{\partial L}{\partial b}=\sum _{t=1}^T\frac{\partial L}{\partial h^{(t)}}\frac{\partial h^{(t)}}{\partial b}=\sum _{t=1}^{T}diag(1-(h^{(t)}{)}^2){\delta }^{(t)}$$
$$\frac{\partial L}{\partial U}=\sum _{t=1}^T\frac{\partial L}{\partial h^{(t)}}\frac{\partial h^{(t)}}{\partial U}=\sum _{t=1}^{T}diag(1-(h^{(t)}{)}^2){\delta }^{(t)}(x^{(t)}{)}^T$$

3. RNN种类：

（1）sequence-to-sequence：输入输出都是一个序列。例如股票预测中的RNN，输入是前N天价格，输出明天的股市价格。

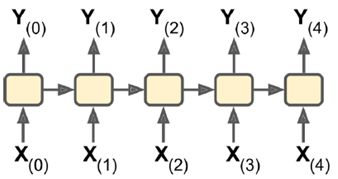
（2）sequence-to-vector：输入是一个序列，输出单一向量。例如，输入一个电影评价序列，输出一个分数表示情感趋势（喜欢还是讨厌）。

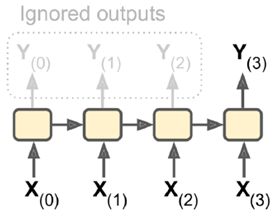
（3）vector-to-sequence：输入单一向量，输出一个序列。

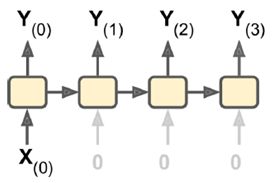
（4）Encoder-Decoder：输入sequence-to-vector，称作encoder，输出vector-to-sequence，称作decoder。
这是一个delay模型，经过一段延迟，即把所有输入都读取后，在decoder中获取输入并输出一个序列。这个模型在机器翻译中使用较广泛，源语言输在入放入encoder，浓缩在状态信息中，生成目标语言时，可以生成一个不等长度的目标语言序列。

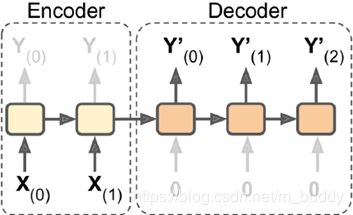
（5）Bidirectional RNNs
RNN 中对于当前时刻 t 通常会考虑之前时刻的信息而没有考虑下文的信息，Bidirectional RNNs 克服了这一缺点，其引入了对下文的考虑，其结构如下：

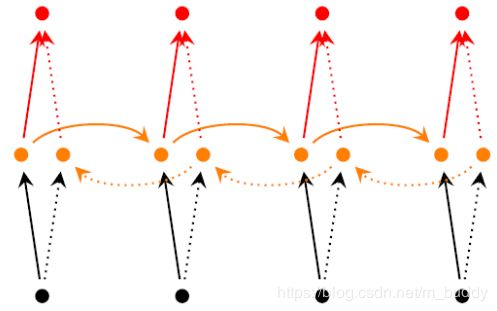
可见 BRNN 引入了一套额外的隐层，但是输入与输出层是共享的，多了一个隐层意味着多了三套参数分别为$U^{\prime },V^{\prime },W^{\prime }$ 。BRNN 的训练算法类似于 RNN ，forward pass 的过程如下：

backward pass 的过程如下：

计算完残差后，分别对前向参数 $U,V,W$ 后向参数 $U^{\prime },V^{\prime },W^{\prime }$ 求导即可，至此 BRNN 的训练算法介绍完毕，目前 ，BRNN 在 NLP 的序列标注任务中取得了极大的成功。

4. RNN在Caffe中的实现与调用

首先来看一下类的层次结构，在Caffe中为LSTM与RNN在基础类Layer的基础上抽象出一个父类RecurrentLayer，然后这两种RNN就在此基础上进行实现。

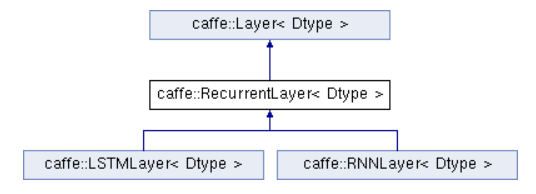
未完待续…

5. 参考REF

1. 循环神经网络(RNN)模型与前向反向传播算法
2. 【机器学习】RNN学习