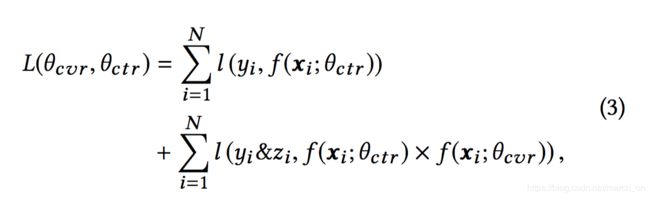Entire Space Multi-Task Model: An E ective Approach for Estimating Post-Click Conversion Rate

ABSTRACT

传统的CVR预估有一些问题，比如训练是在被点击的曝光上进行，而预估是在所有曝光上。这就是sample selection bias 问题。另外，还有一个数据稀疏问题，使得训练比较困难。文中作者从一个全新的角度对CVR建模，利用用户行为的顺序模式，曝光->点击->转化，进而提出了**Entire Space Multi-task Model (ESMM) ** 模型，并通过如下两种方式解决上面的两个问题：
1.直接在全部样本上进行优化；
2.使用了一种特征表示迁移学习方法。
在淘宝推荐系统上的数据集上的实验证明了模型的有效性。并释放了一个数据集。

INTRODUCTION

为了解决CVR预估中的样本选择偏置（SSB）和数据稀疏（DS）问题，作者提出了ESMM模型。在该模型中，引入了两个辅助任务：预估曝光后的CTR和曝光后的CTR&CVR。不再像之前直接在点击样本上训练，ESMM把pCVR作为一个中间变量，该变量乘以pCTR 就是 pCTCVR。pCTR和pCTCVR两个问题都是在所有曝光样本组成的整个问题空间上进行预估的，所以由此得到PCVR也是适用到整个空间的。这样SSB问题就解决了。另外，CVR的特征表示的参数和CTR是共享的，而CTR的样本更多，这种参数迁移学习的方法可以极大减轻数据稀疏问题。
从淘宝推荐系统上收集的数据集有89亿样本，包含了点击和下单label。

THE PROPOSED APPROACH

Notation

假设数据集是

样本(x,y->z),N是曝光数，x是曝光样本的特征向量，y、z分别是点击和下单label，
y-> z表示点击和下单之间的顺序依赖，即只有点击之后才会有下单。
CVR 预估是指pCVR = p(z=1|y=1, x)。 然后 有两个关联的概率：PCTCVR和 PCTR

CVR Modeling and Challenges

常见的CVR预估建模的是p(z=1|y=1,x),是在点击的曝光样本上进行的，$S_c=(x_j,z_j)|y_j=1{|}_{j=1}^M$ 。M是点击数。$S_c$是$S$的子集，其中，下单的曝光为正样本，没曝光的点击是负样本。其实

这种方法有如下问题：

Sample selection bias (SSB)

传统的CVR其实是做了一个近似
$$p(z=1|y=1,x)\approx p(z=1|x_c)（1）$$
引入的辅助特征空间$X_c$其实和$S_c$是对应的。任意属于$X_c$的样本$x_c$都存在一个$(x=x_c,y_x=1)$,$y_x$是x的点击label。所以$q(z=1|x)$就是在$X_c$空间下训练的。在预估阶段$p(z=1|y=1,x)$是在整个空间X上进行的，等同于$p(z=1|x)$.暗含了对于任意点击样本$(x=x_c,y_x=1)$ 中 $x\in X$ 且$x\in X_c$ 这样一个假设。

总结起来一句话，就是训练的时候是在点击样本中训练的 预估的时候是在所有曝光样本上进行的。假设训练阶段的这些点击样本 $S_c$ 学习到一个特征空间$X_c$，那么预估的时候的假设就是这些点击样本还是来自于训练阶段学习到的样本空间$X_c$。

这个假设很可能不成立，因为$X_c$只是全部特征空间$X$的一小部分，会被那种很少发生的点击事件的随机性严重影响，这种点击是可能发生在整个空间$X$中的。同时，由于实际没有足够的样本，$X_c$可能跟$X$差别很大。这样，训练时的分布和真实分布就有一个偏差（drift），影响模型的泛化。

Data sparsity (DS)

这个比较好理解。

作者提到了CVR 的其他问题delayed feedback 这个不是文中研究的内容。

Entire Space Multi-Task Model

模型结构图见上图。

从多任务学习中获得灵感。该模型引入了两个子任务，CTR 和CTCVR，同时解决之前的两个问题。

总体上来说，ESMM 对一个曝光会同时输出pCTR ，pCVR 和pCTCVR。

包含了两个网络：左边的CVR和右边的CTR。
这两个网络都和base model 的网络结构相同。CTCVR 将两个网络的乘积作为预估值。
该模型有以下几个亮点（highlights)

Modeling over entire space.

$p(z=1，y=1,x)$ 和$p(y=1|x)$ 是在所有曝光样本上学习的。通过上式，我们可以得到CTCVR 和CTR， 这样CVR也就能在整个输入空间$X$中得到了，这样， SSB问题也就解决了。简单一点的话，我们对CTCVR和CTR 各自使用模型进行学习，最后通过上式得到CVR。这个模型我们称作DIVISION 而上式是通过除法得到CVR的，其中分母 CTR 是一个很小的数，这样可能会有数值不稳定问题。ESMM 使用乘积的形式来避免这个问题。

在ESMM中，CVR是一个中间变量，CTCVR和CTR才是ESMM在整数输入空间上预估的因子。The multiplication form enables the three associated and co-trained estimators to exploit the sequential patten of data and communicate information with each other during training. 另外，乘积形式可以保证pCVR的预估值在(0,1)之间，除法形式可能超过1。

ESMM 的损失函数如上所示。${\theta }_{ctr}$和${\theta }_{cvr}$是CTR和CVR网络的参数，而$l$是交叉熵损失。

Feature representation transfer

ESMM中CVR和CTR 网络共享embedding参数。

This parameter sharing mechanism enables CVR network in ESMM to learn from un-clicked impressions and provides great help for alleviating the data sparsity trouble.

EXPERIMENTS

3.1 Experimental Setup

作者调研时没有包含点击和下单label的数据集，所以他们从淘宝推荐系统搜集数据并随机采样了1%的流量作为数据集发布。仍然有38G，文中将发布的数据集称为public dataset， 全量数据集为Product dataset。

基线模型

BASE 模型就是ESMM图中左侧的模型结构
AMAN 使用负采样
OVERSAMPLING 使用过采样，复制正样本，
UNBIAS follows [10] to t the truly underlying distribution from observations via rejection sampling.拒绝采样不懂
DIVISION 是分开训练CTR和CTCVR 模型，并按除法来计算CVR。

ESMM-NS 是不共享embedding参数的ESMM模型

前四种方法是直接在当前的DNN架构上对CVR进行建模的不同变种（variation）
DIVISION/ESMM-NS/ESMM 都是在整个输入空间上对CVR 建模，涉及到3个网络：CTR、CVR和CTCVR。

ESMM-NS, ESMM 共同训练这3个模型，并把CVR网络的输出作为对比。

为了公平，包括ESMM在内的所有模型都使用相同的网络结构和超参数：
使用RELU作为激活函数
embedding向量大小为18.
MLP中隐层大小为[360,200,80,2]
使用 adam 优化，超参数是 β1 = 0.9, β2 = 0.999, ε = 10−8.

Metric
分两个任务来对比：
1.传统CVR任务，在点击样本上预估CVR。

2.CTCVR， 在所有曝光数据上预估CTCVR。

任务2 在整个输入空间上对比，反应不同模型在SSB问题上的效果
CTCVR 的计算方式是pCTR*pCVR.其中，
1.CVR是各个模型单独预估的
2.CTR 是独立训练的相同的CTR 网络预估的（和Base 模型相同的网络结构和超参数）
所有两个任务都将时间序列上的前1/2作为训练集，剩下的作为测试集。

是说时间上前一半的数据是训练集，后一半是测试集？？

AUC作为评价指标。所有实验都重复10次，取最后的均值作为模型效果；

Results on Public Dataset

1.base模型的3个变种，除了AMAN 在CVR 上稍差以外，其他的在CVR和CTCVR 上都比base 好。
2. DIVISION and ESMM-NS 都在整个输入空间上对CVR建模，都显著好于base模型。由于避免了数值不稳定问题，ESMM-NS效果更好
3. ESMM 进一步提升了ESMM-NS

Results on Product Dataset

product dataset 包含89亿样本。

为了证实训练集大小的影响，作者尝试了不同的采样率。

可以看到，随着采样率提升，所有模型效果都有提升，表明数据稀疏问题的影响。
1.除了AMAN 在1% 采样率的CVR 任务上，其他模型在所有配置上都好于base。
2.ESMM-NS 和ESMM 在不同采样率上都好于其他模型。ESMM模型在两个任务上的优势都更加明显。

CONCLUSIONS AND FUTURE WORK

In the future, we intend to design global optimization models in applications with multi- stage actions like request → impression → click → conversion