深度学习小白——神经网络5(参数更新)
一、参数更新
1.随机梯度下降及各种更新方法
【普通更新】:沿着负梯度方向改变参数
x+= -learning_rate * dx
其中学习率是一个超参数,它是一个固定的常量。
【动量更新】(Momentum)
这个方法在深度网络上几乎总能得到更好的收敛速度。是从物理角度上对最优化问题得到的启发。它将损失值理解为是山的高度(因此高度势能是U=mgh,所以U正比于h)用随机数字初始化参数等同于在某个位置给质点设定初始速度为0,这样,最优化过程可以看做是模拟参数向量(即质点)在地形上滚动的过程
因为作用于质点的力与梯度的潜在能量(F=-▽U)有关,质点所受的力就是损失函数的(负)梯度。还有,因为F=ma,所以在这个观点下,梯度与质点的加速度是成比例的。与SDG不同的是,此处认为梯度只是影响速度,然后速度再影响位置。
# 动量更新
v = mu * v - learning_rate * dx # 与速度融合
x += v # 与位置融合【Nesterov动量】最近变得流行,在实践中比标准动量表现更好一些
核心思路: 但当参数向量位于某个位置x时,由上述公式知,动量部分会通过mu*v稍微改变参数向量。因此,如果要计算梯度,那么可以将未来的近似位置x+mu*V看做是“向前看”,这个点在我们一会要停止的位置附近,因此计算x+mu*v的梯度而不是旧位置x的梯度就有意义了。
如右图,既然我们知道动量将会把我们带到绿色箭头指向的店,我们就不要再远点(红色点)那里计算梯度了。
x_ahead = x + mu * v
# 计算dx_ahead(在x_ahead处的梯度,而不是在x处的梯度)
v = mu * v - learning_rate * dx_ahead
x += v实际应用中,通过对x_ahead=x+mu*v使用变量变化进行改写,然后用x_ahead而不是x来表示上面的更新,也就是说实际存储的参数向量总是向前一步的那个版本,x_ahead(将其重新命名为x)的公式就变成了:
v_prev = v # 存储备份
v = mu * v - learning_rate * dx # 速度更新保持不变
x += -mu * v_prev + (1 + mu) * v # 位置更新变了形式二、学习率退火
如果学习率过高,系统的动能就过大,参数向量就会无规律地跳动,不能够稳定到损失函数更深更窄的部分去。实现学习率退火有3种方式:
1.随步数衰减
典型的值是每过5个周期就将学习率减小一半,但这要依赖具体问题和模型的选择。有一种经验做法:使用一个固定的学习率来进行训练的同时观察验证集错误率,每当验证集错误率停止下降,就乘以一个常数(0.5)来降低学习率
2.指数衰减
,t是迭代次数
3.1/t衰减
三、二阶方法
基于牛顿法,其迭代如下:
Hf(x)是函数的二阶偏导数的平方矩阵,▽f(x)是梯度向量,直观理解Hf(x)描述了损失函数的局部曲率,从而使得可以进行更高效的参数更新。使得在曲率大的时候小步前进,曲率小的时候大步前进。但一个巨大难题在于要计算矩阵的逆,这是非常耗时的。这样,各种各样的拟-牛顿方法就被发明出来,最流行的是L-BFGS.
四、逐参数适应学习率方法
前面讨论都是对学习率进行全局地操作,并且对所有的参数都是一样的。有一些人发明了能够适应性对学习率调参的方法,甚至是逐个参数适应学习率调参。如下是一些常用的适应算法
1.Adagrad
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)接收到高梯度值的权重更新的效果被减弱,而接受到低梯度值的权重的更新效果将会增强
2.RMSprop
简单修改了Adagrad方法,让它不那么激进,总体来说,就是是使用了一个梯度平方的滑动平均:
cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)3.Adam
像是RMSprop的动量版
m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)五、超参数调优
神经网络最常用的超参数有:
- 初始学习率
- 学习率衰减方式(例如一个衰减常量)
- 正则化强度(L2惩罚,随机失活强度)
超参数范围
在对数尺度上进行超参数搜索。例如,一个典型的学习率应该看起来是这样:learning_rate=10** uniform(-6,1),因为学习率乘以了计算出的梯度,因此,比起加上或者减少某些值,思考学习率的范围是乘以或者除以某些值更加自然。但是有一些参数(比如随机失活概率)还是在原始尺度上进行搜索
随机搜索优于网络搜索
对于边界上的最优值要小心,这种情况一般发生在你在一个不好的范围内搜索超参数。比如,假设我们使用learning_rate=10** uniform(-6,1)来进行搜索。一旦我们得到一个比较好的值,一定要确认你的值不是出于这个范围的边界上。
从粗到细地分阶段搜索。在实践中,先进行初略范围搜索,然后根据好的结果出现的地方,缩小范围进行搜索。进行粗搜索的时候,让模型训练一个周期就可以了,小范围搜索时,可以让模型运行5个周期,而最后一个阶段就在最终的范围内进行仔细搜索,运行多次周期。
六、评价
模型集成
在实践的时候,有一个总是能提升神经网络几个百分点准确率的办法,就是在训练的时候训练几个独立的模型,然后在测试的时候平均它们预测结果。集成的模型数量增加,算法的结果也单调提升(但提升效果越来越少)。还有模型之间的差异度越大,提升效果可能越好。进行集成有以下几种方法:
- 同一个模型,不同的初始化:使用交叉验证来得到最好的超参数,然后用最好的参数来训练不同初始化条件的模型
- 在交叉验证中发现最好的模型:使用交叉验证来得到最好的超参数,然后取其中最好的几个(比如10个)模型来进行集成。这样就提高了集成的多样性,实际操作中,这样操作起来比较简单,在交叉验证后就不需要额外的训练
- 一个模型设置多个记录点:如果训练非常耗时,那就在不同的训练时间对网络留下记录点(比如每个周期结束),然后用它们来进行模型集成。很显然,这样做多样性不足,但是在实践中效果还是不错的,这种方法的优势是代价比较小
- 在训练的时候跑参数的平均值:这个方法就是在训练过程中,如果损失值相较于前一次权重出现指数下降时,就在内存中对网络的权重进行一次备份,这样你就对前几次循环中的网络状态进行了平均。你会发现这个“平滑”过的版本的权重总是能得到更少的误差。
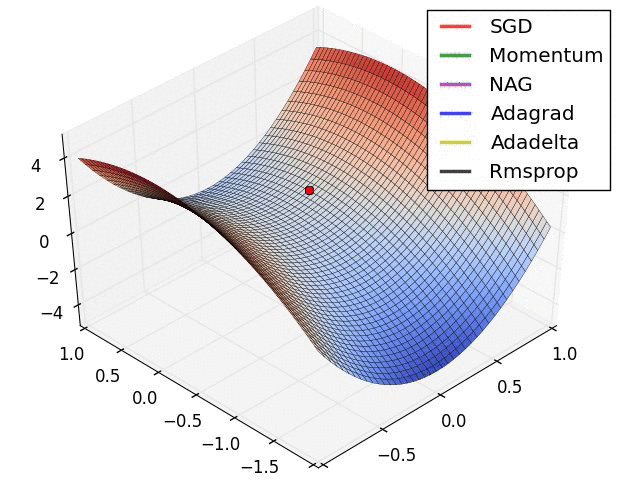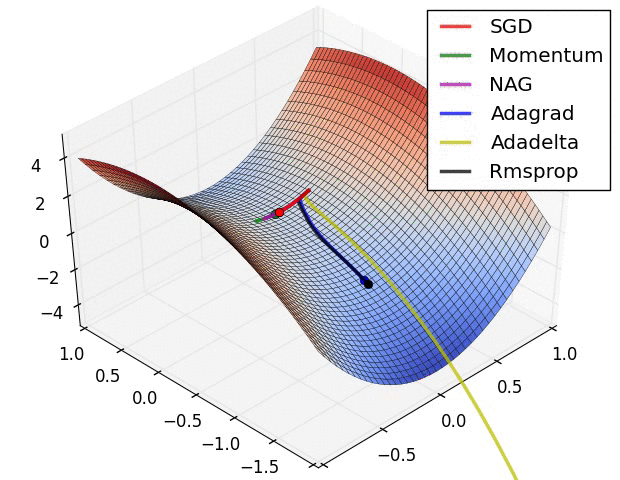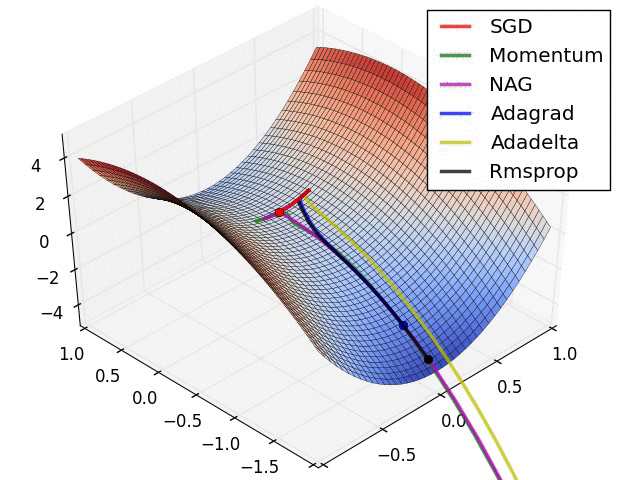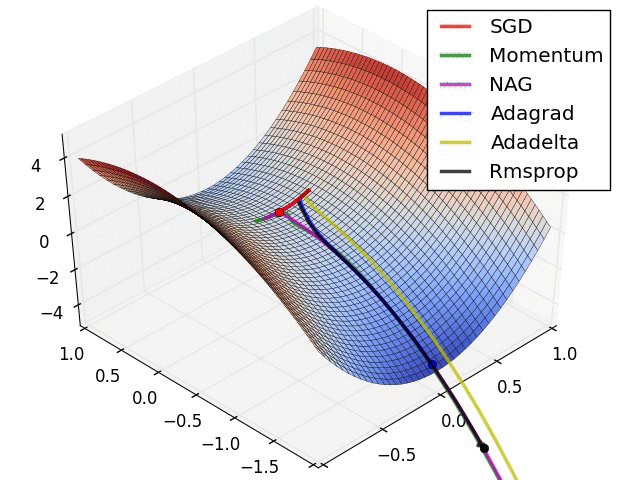
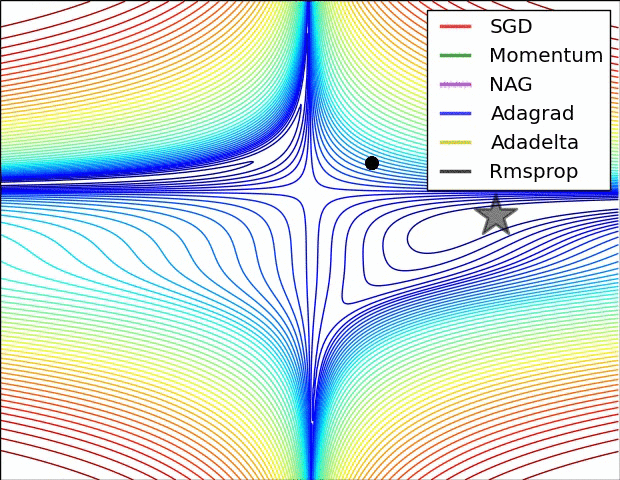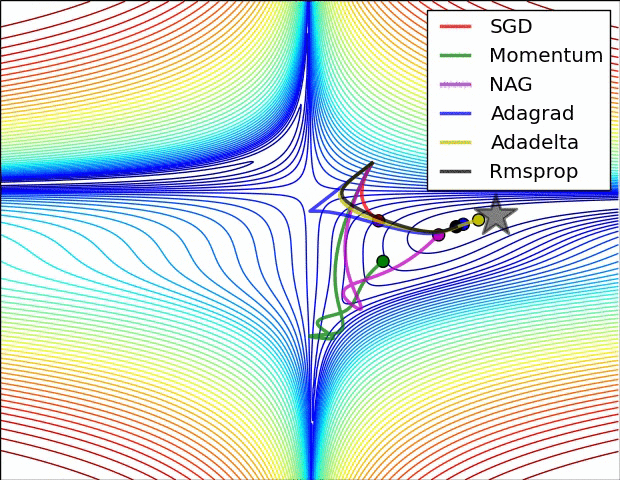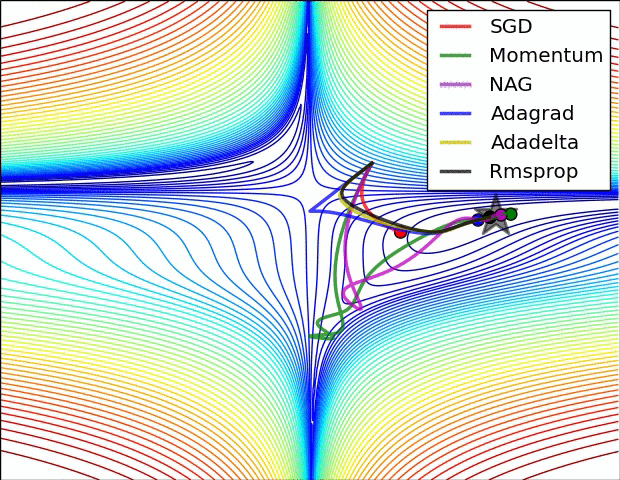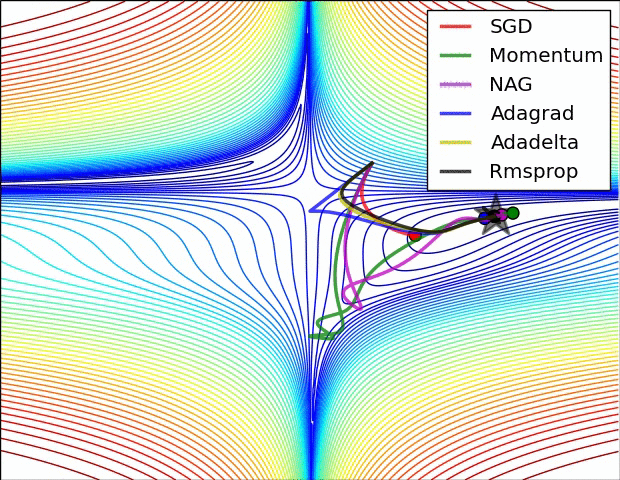
【这两幅动图帮助你理解学习的动态过程】
七、总结
训练一个神经网络需要:
-
利用小批量数据对实现进行梯度检查,还要注意各种错误。
-
进行合理性检查,确认初始损失值是合理的,在小数据集上能得到100%的准确率。
-
在训练时,跟踪损失函数值,训练集和验证集准确率,如果愿意,还可以跟踪更新的参数量相对于总参数量的比例(一般在1e-3左右),然后如果是对于卷积神经网络,可以将第一层的权重可视化。
-
推荐的两个更新方法是SGD+Nesterov动量方法,或者Adam方法。
-
随着训练进行学习率衰减。比如,在固定多少个周期后让学习率减半,或者当验证集准确率下降的时候。
-
使用随机搜索(不要用网格搜索)来搜索最优的超参数。分阶段从粗(比较宽的超参数范围训练1-5个周期)到细(窄范围训练很多个周期)地来搜索。
-
进行模型集成来获得额外的性能提高。