张量分解 （Tensor）

一般一维数组，称之为向量（vector）,

二维数组，称之为矩阵（matrix）;

三维数组以及多位数组，我们称之为张量（tensor）。

一、基本概念

矩阵补全（Matrix Completion）目的是为了估计矩阵中缺失的部分（不可观察的部分），可以看做是用矩阵X近似矩阵M，然后用X中的元素作为矩阵M中不可观察部分的元素的估计。

矩阵分解（Matrix Factorization）是指用 A*B 来近似矩阵M，那么 A*B 的元素就可以用于估计M中对应不可见位置的元素值，而A*B可以看做是M的分解，所以称作Matrix Factorization。

这是因为协同过滤本质上是考虑大量用户的偏好信息（协同），来对某一用户的偏好做出预测（过滤），那么当我们把这样的偏好用评分矩阵M表达后，这即等价于用M其他行的已知值（每一行包含一个用户对所有商品的已知评分），来估计并填充某一行的缺失值。若要对所有用户进行预测，便是填充整个矩阵，这是所谓“协同过滤本质是矩阵填充”。

那么，这里的矩阵填充如何来做呢？矩阵分解是一种主流方法。这是因为，协同过滤有一个隐含的重要假设，可简单表述为：如果用户A和用户B同时偏好商品X，那么用户A和用户B对其他商品的偏好性有更大的几率相似。这个假设反映在矩阵M上即是矩阵的低秩。极端情况之一是若所有用户对不同商品的偏好保持一致，那么填充完的M每行应两两相等，即秩为1。

所以这时我们可以对矩阵M进行低秩矩阵分解，用U*V来逼近M，以用于填充——对于用户数为m，商品数为n的情况，M是m*n的矩阵，U是m*r，V是r*n，其中r是人工指定的参数。这里利用M的低秩性，以秩为r的矩阵M’=U*V来近似M，用M’上的元素值来填充M上的缺失值，达到预测效果。

二、矩阵分解常用方法

Basic mf

Basic MF是最基础的分解方式，将评分矩阵R分解为用户矩阵U和项目矩阵S， 通过不断的迭代训练使得U和S的乘积越来越接近真实矩阵，矩阵分解过程如图：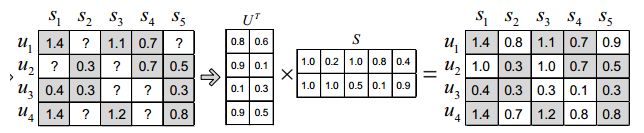

预测值接近真实值就是使其差最小，这是我们的目标函数，然后采用梯度下降的方式迭代计算U和S，它们收敛时就是分解出来的矩阵。我们用损失函数来表示误差（等价于目标函数）：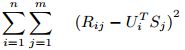

上式中R_ij是评分矩阵中已打分的值，U_i和S_j相当于未知变量。为求得公式1的最小值，相当于求关于U和S二元函数的最小值（极小值或许更贴切）。通常采用梯度下降的方法：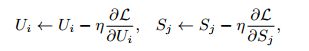

依他 是学习速率，表示迭代的步长。其值为1.5时，通常以震荡形式接近极值点；若<1迭代单调趋向极值点；若>2围绕极值逐渐发散，不会收敛到极值点。具体取什么值要根据实验经验。

Regularized mf

正则化矩阵分解是Basic MF的优化，解决MF造成的过拟合问题。其不是直接最小化损失函数，而是在损失函数基础上增加规范化因子，将整体作为损失函数。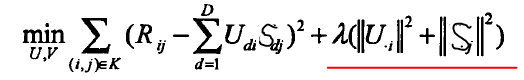

红线表示正则化因子，在求解U和S时，仍然采用梯度下降法，此时迭代公式变为：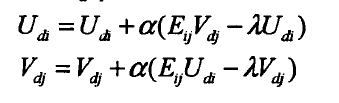

其中，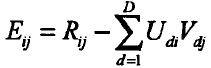

梯度下降结束条件：f(x)的真实值和预测值小于自己设定的阈值

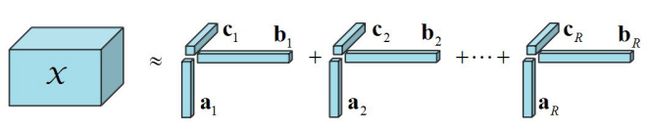
三、张量CP分解

CP分解的张量形式：
将一个张量表示成有限个秩一张量之和，比如一个三阶张量可以分解为

CP分解的矩阵形式:
因子矩阵：秩一张量中对应的向量组成的矩阵，如

利用因子矩阵，一个三阶张量的CP分解可以写成展开形式

CP分解的计算：
以一个三阶张量X为例，假定成分个数R已知，目标为:

作为ALS的一个子问题，固定B和C，求解A;固定A和C求解B；再固定B和C求解A。比如固定B和C，求解A如下:

得到：

再通过归一化分别求出A和

四、张量Tucker分解

Tucker分解是一种高阶的主成分分析，它将一个张量表示成一个核心（core）张量沿每一个mode乘上一个矩阵。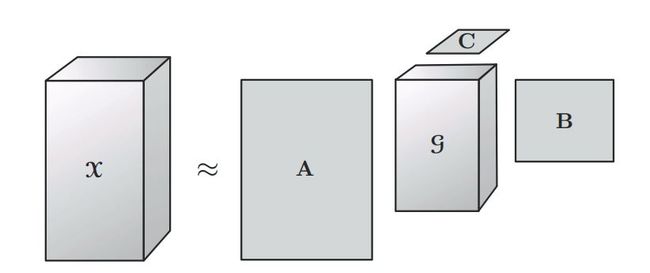

对于三阶张量 来说，其Tucker分解为

容易看出，CP分解是Tucker分解的一种特殊形式：如果核心张量是对角的，且P=Q=R，则Tucker分解就退化成了CP分解。

Tucker分解的矩阵形式
三阶Tucker分解的展开形式为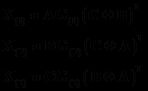

Tucker分解可以推广到高阶张量

Tucker分解的计算
HOSVD：利用SVD对每个mode做一次Tucker1分解（截断或者不截断）。HOSVD不能保证得到一个较好的近似，但HOSVD的结果可以作为一个其他迭代算法（如HOOI）的很好的初始解。

为了导出HOOI迭代算法，先考虑目标函数：

从而应该满足

目标函数的平方变为：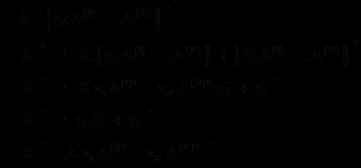

所以问题可以进行如下转化：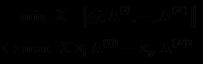

利用交替求解的思想，问题变为解如下子问题:

五、张量分解应用

问题描述：通过司机历史轨迹预测司机在某条轨迹的行驶时间。这里面有一个重要的问题，那就是数据稀疏性问题，因为司机不可能走过所有的道路，此时就用到张量分解。

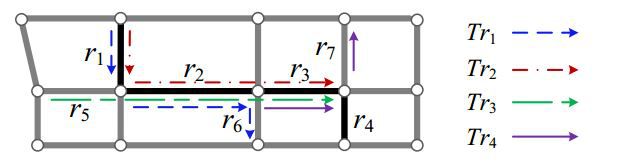
如上图，这里有四条轨迹，我们需要根据这几条轨迹，预测r1->r2->r3->r4这条轨迹的行驶时间，发现r4是没有走过的，此时就需要用某个方法预测出来。

构造一个三维张量：。张量的三个维度分别为：路段ID,时间段，司机。

将张量分解为一个核心张量，和三个矩阵：

选择用Tucker分解，目标函数如下：

其中是加的正则向，避免过拟合。

因此，

分解完整算法如下：

1、Tamara G. Kolda， Brett W. Bader .Tensor Decompositions and Applications
2、彭毅 张量分解（ppt）
3、Yilun Wang,Yu Zheng.Travel Time Estimation of a Path using Sparse Trajectories 2014 KDD