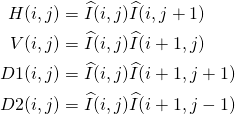图像质量评估：BRISQUE
拍照很容易，但拍摄高质量的照片很难。它需要良好的构图和照明。合适的镜头和卓越的设备可以产生很大的不同。但最重要的是，高质量的照片需要良好的品味和判断力。你需要一个专家的眼睛。
在这篇文章中，我们将学习一种预测图像质量得分的算法。
什么是图像质量评估（IQA）？
图像质量评估（IQA）算法将任意图像作为输入，并输出质量分数作为输出。有三种类型的IQA：
- 全参考IQA： 有一个非失真的参考图像来测量失真图像的质量，可用于评估图像压缩算法的质量。
- 降低参考IQA： 没有参考图像，而是具有一些选择性信息的图像（例如水印图像），用于比较和测量失真图像的质量。
- 目标盲目或无参考IQA： 算法获得的唯一输入是要测量其质量的图像。
无参考IQA
在这篇文章中，我们将讨论一个无参考IQA指标，称为盲/无参考图像空间质量评估器（BRISQUE）。在我们深入理论之前，让我们先了解两个基本术语：
- 扭曲图像：顾名思义，扭曲图像是原始图像的一种版本，它会因模糊，噪声，水印，颜色变换，几何变换等而失真。
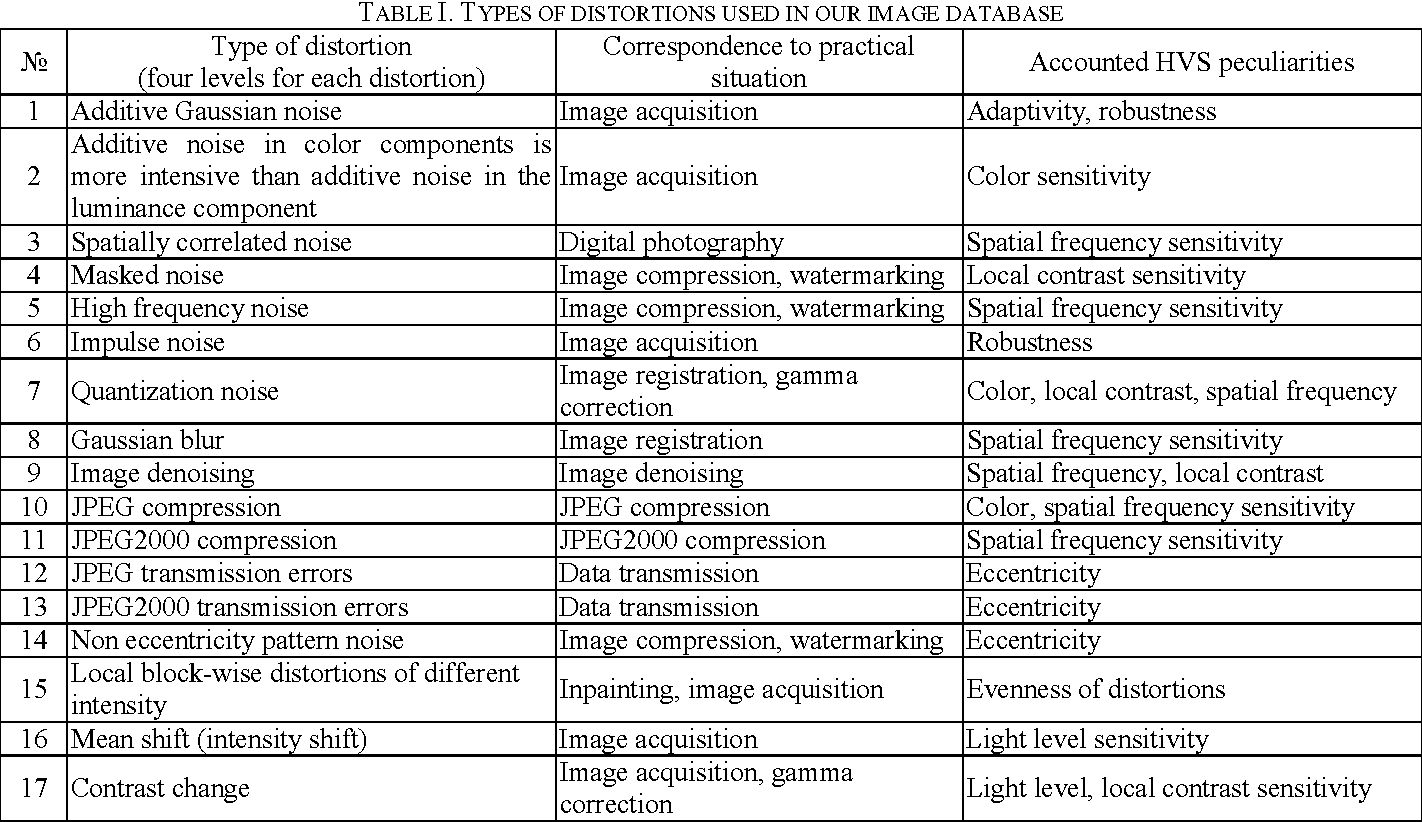
图1 TID 2008数据库中使用的扭曲
- 自然图像：在没有后期处理的情况下由相机直接拍摄的图像。这是自然图像和失真图像的示例。
图2自然图像（左）和噪声图像（失真，右）
可以想象，图像是否扭曲或自然是不是很清晰。例如，当使用运动模糊智能地渲染视频时，由于故意模糊，算法可能会对其质量感到困惑。因此，必须在正确的背景下使用此质量测量。
图像质量评估（IQA）数据集
图3 TID2008图像质量得分缩放（0到100）：得分越小，主观质量越好。
质量是一个主观问题。为了训练好的模型，需要为获取图像的质量得分。
谁为这些训练图像分配了质量得分？当然是人类。但我们不能仅仅依靠一个人的意见。因此，我们需要几个人的意见，并为图像分配0（最佳）和100（最差）之间的平均分数。该分数在学术文献中称为平均质量分数。
TID2008的数据集就是一个这样的训练集。
盲/无参考图像空间质量评估器（BRISQUE）
在本节中，将描述用于无参考IQA的BRISQUE算法所需的步骤。
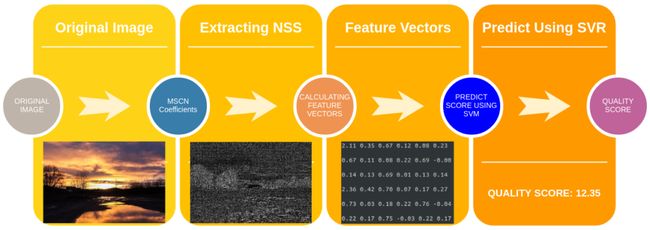
图5显示了计算BRISQUE所涉及的步骤。
图4使用BRISQUE模型计算图像质量得分的步骤
第1步：提取自然场景统计（NSS）
自然图像的像素强度的分布不同于失真图像的像素强度的分布。当我们归一化像素强度并计算这些归一化强度上的分布时，这种分布差异更加明显。特别地，在归一化之后，自然图像的像素强度遵循高斯分布（贝尔曲线），而不自然或失真图像的像素强度不遵循高斯分布（贝尔曲线）。
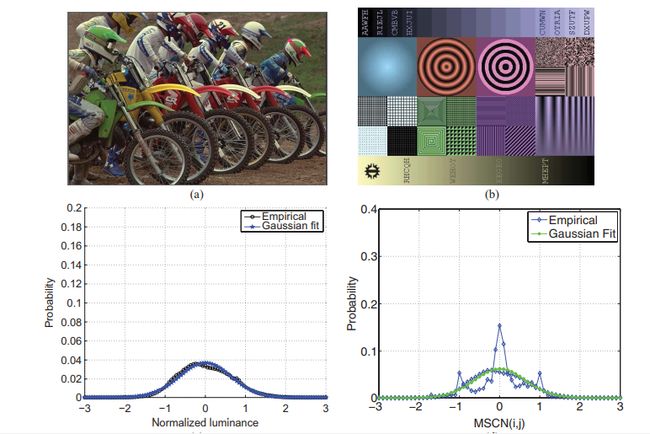
在下图中显示了这一点。
图5左侧：显示没有添加人工效果的自然图像，符合高斯分布。右图：人工图像，不适合相同的分布。
平均取代对比度标准化（MSCN）
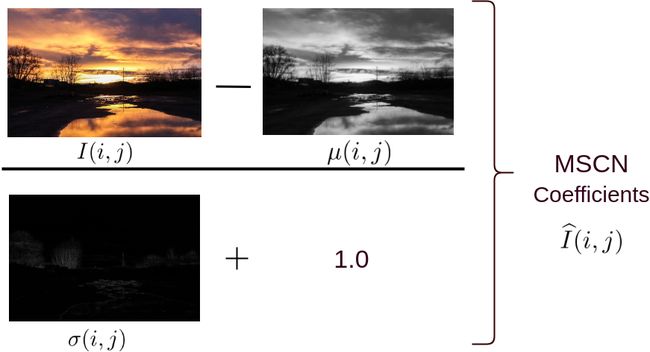
有几种不同的方法来规范化图像。一种这样的归一化称为平均取代对比度归一化（MSCN）。下图显示了如何计算MSCN系数。
图6计算MSCN系数的步骤
这可以看作如下：
图7 MSCN系数的计算
为了计算MSCN系数，将
像素处的图像强度
变换为亮度
。
（1） 
其中
（M和N分别是高度和宽度）。
和
分别为局部平均和局部方差。局部平均（
）只是原始图像的高斯模糊，而局部方差（
）是原始图像和局部平均差异的平方的高斯模糊。在下面的等式中
是高斯模糊窗口函数。
（2） 
MSCN为像素强度提供了良好的归一化。然而，自然与失真图像的差异不仅限于像素强度分布，还包括相邻像素之间的关系。
为了捕获相邻像素的关系，使用四个方向相邻元素的乘积，即：水平（H），垂直（V），左 - 对角线（D1），右 - 对角线（D2）。
（3） 
第2步：计算特征向量
到目前为止，我们已经从原始图像中获得了5个参数 - 1个MSCN参数和4个相邻元素乘积参数（水平，垂直，左对角线，右对角线）。
接下来，我们将使用这5个参数来计算尺寸为36×1的特征向量。请注意，原始输入图像可以是任何尺寸（宽度/高度），但特征向量的大小始终为36×1。
通过将MSCN参数拟合到广义高斯分布（GGD）来计算36×1特征向量的前两个元素。GGD有两个参数 - 一个用于形状，一个用于方差。
接下来，非对称广义高斯分布（AGGD）适合于4个相邻元素乘积参数中的每一个。AGGD是广义高斯拟合（GGD）的不对称形式。它有四个参数 - 形状，均值，左方差和右方差。由于有4个成对产品图像，我们最终得到16个值。
因此，我们最终得到了18个特征向量元素。将图像缩小到原始尺寸的一半，并重复相同的过程以获得18个新数字，使总数达到36个数字。
这在下表中总结。
| 特征范围 | 功能描述 | 程序 |
|---|---|---|
| 1 - 2 | 形状和方差。 | GGD拟合MSCN参数。 |
| 3 - 6 | 形状，均值，左方差，右方差 | AGGD拟合水平参数 |
| 7 - 10 | 形状，均值，左方差，右方差 | AGGD拟合垂直参数 |
| 11 - 14 | 形状，均值，左方差，右方差 | AGGD拟合对角线（左）参数 |
| 15-18 | 形状，均值，左方差，右方差 | AGGD拟合对角线（右）参数 |
第3步：预测图像质量得分
在典型的机器学习应用程序中，首先将图像转换为特征向量。然后，将训练数据集中的所有图像的特征向量和输出（质量得分）放入支持向量机（SVM）中进行训练。
使用LIBSVM加载该36个特征参数及质量得分进行训练，训练过程中，特征向量首先被缩放到-1到1，训练得出的模型用于预测图像质量。
经过训练模型预测，可以得出以下每种失真的最终质量得分：
| 原始图像 | JPEG2K压缩 | 重压缩 | 高斯噪声 | 中位数模糊 |
|---|---|---|---|---|
 |
 |
 |
 |
 |
| 26.8286 | 30.7417 | 33.0692 | 79.8751 | 72.7044 |