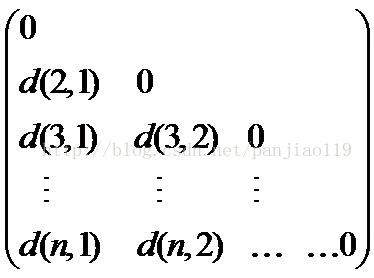K-means 和 K-medoids算法聚类分析

 1    聚类是对物理的或者抽象的对象集合分组的过程，聚类生成的组称为簇，而簇是数据对象的集合。

        （1）簇内部的任意两个对象之间具有较高的相似度。（2）属于不同的簇的两个对象间具有较高的相异度。

 2    相异度可以根据描述对象的属性值来计算，最常用的度量指标是距离。

 3   聚类最初来自数学，统计学，和数值分析；机器学习领域把聚类描述成隐含模式，发现簇的过程是无监督学习；聚类是模式识别的重要手段。

 4    聚类的特点：用少量的簇来描述大量数据的特征：  数据简洁，丢失精细部分

 5   聚类数据挖掘实践中的应用

   （1） 数据预处理  （2） 科学数据探索 （3） 信息获取与文本挖掘  （4）  空间数据库应用 

   （5） 客户关系管理 （6） 市场分析  （7）  Web分析  （8）  医学诊断  （9）计算生物学。

6   统计学 ：  聚类分析是通过数据建模简化数据的一种方法：包括  系统聚类法，分解法，加入法，动态聚类法。有序样品聚类，有重叠聚类和模糊聚类等

7   机器学习：簇  相当于隐藏模式。聚类是搜索簇的无监督学习的过程

      与 分类不同。无监督学习不依赖预先定义的类或者带类标记的训练实例。需要有聚类学习算法自动确定标记。而分类学习

的实例或数据对象有类别标记。聚类是观察试学习，而不是实例式学习。

8   实际应用：聚类分析是数据挖掘的主要任务之一

    （1） 作为一个独立的工具获得数据的分布状况。观察每一个簇数据的特征，集中对特定的簇集合作进一步地分析。

     （2） 作为其他数据挖掘任务（如分类，关联规则）的预处理步骤

9   聚类算法的特征：

    （1）处理不同类型属性的能力；

    （2） 对大型数据集的可扩展性；
    （3） 处理高维数据的能力；
    （4） 发现任意形状簇的能力；
    （5） 处理孤立点或“噪声”数据的能力；
             对“噪声”数据具有较低的敏感性；
             合理地发现孤立点。
    （6） 对数据顺序的不敏感性；
    （7） 对先验知识和用户自定义参数的依赖性；
    （8） 聚类结果的可解释性和实用性；
    （9） 基于约束的聚类。

10  聚类算法分类：

    (1)  基于划分的方法：  K-means 算法    基于密度的算法

   （2） 基于层次的方法 ：  凝聚算法  分裂算法

   （3） 基于网络的 方法

   （4） 非数据与数据属性同时出现的方法

    （5）基于约束的方法

   （6） 运用机器学习技术的方法  ：梯度下降法  人工神经网络   进化模型

    （7） 有扩展性的算法

    （8） 面向高维数据集的算法

10   数据类型

     （1）区间标度型：用线性标度描述的连续度量  （如  高度   重量 经纬度坐标 温度等）

     （2）  布尔类型 ： 如果两个状态同等重要，称为对称的  否则是不对称的

     （3）  标称型： 有若干个离散的取值

     （4） 序数型：  取离散的序数值，序列排序是有意义的

     （5） 比例标度型：在非线性标度上取正的度量值。

11  数据结构   

                                      数据矩阵                                                                                                                                   相异度矩阵

                          

12     距离函数  （计算对象之间的距离）

   距离函数‖‖应满足的条件：
   (1)‖xi–xj‖=0，当且仅当xi=xj
   (2)非负性：‖xi–xj‖≥0
   (3)对称性：‖xi–xj‖=‖xj–xi‖
   (4)三角不等式：
      ‖xi–xk‖≤‖xi–xj‖+‖xj–xk‖

13   设两个对象的p维向量分别表示为
  xi=(xi1,xi2,…,xip)T和xj=(xj1,xj2,…,xjp)T，
有多种形式的距离度量可以采用。如，
闵可夫斯基（Minkowski）距离
曼哈坦（Manhattan）距离
欧几里得（Euclidean）距离
切比雪夫（Chebyshev）距离
马哈拉诺比斯（Mahalanobis）距离

 14   距离计算公式

       

15  令对象的维数p=2，在二维空间中考察到原点距离为常数的所有点形成的形状。即，考察集合{x| ||x||=c}的形状。

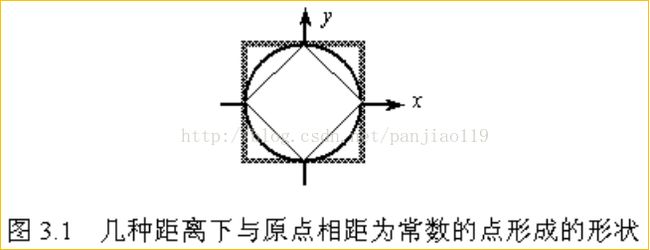
菱形：曼哈坦距离；                                        圆形：欧几里德距离；                                方形：切比雪夫距离

16     基于划分的聚类方法

      划分方法：已知由n个对象(或元组)构成的数据库，对其采用目标函数最小化的策略，通过迭代把数据分成k个划分块，每个划分块为一个簇(cluster)。
      划分方法满足两个条件： （1）每个簇至少包含一个对象；   （2）每个对象必需属于且仅属于某一个簇。
      常见的划分方法：  （1）k-means(k-均值)方法                       （2）  k-medoids(k-中心点)方法

17  k-means聚类算法

      k-均值(K-means)聚类算法的核心思想：通过迭代把数据对象划分到不同的簇中，以求目标函数最小化，从而使生成的簇尽可能地紧凑和独立。
设p表示数据对象，ci表示簇Ci的均值，通常目标函数采用平方误差准则函数：

                                                                                     
 
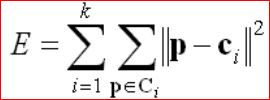
这个目标函数采用欧几里得距离度量。如果采用Mahalanobis距离可以对椭圆形的簇进行分析。

18     k-means算法步骤：
        首先，随机选取k个对象作为初始的k个簇的质心；
        然后，将其余对象根据其与各个簇质心的距离分配到最近的簇；再求新形成的簇的质心。
        这个迭代重定位过程不断重复，直到目标函数最小化为止。

19   K-means算法
       输入：期望得到的簇的数目k，n个对象的数据库。
       输出：使得平方误差准则函数最小化的k个簇。

       方法：选择k个对象作为初始的簇的质心；

              Repeat    （1）计算对象与各个簇的质心的距离，将对象划分到距离其最近的簇；
                              （2）重新计算每个新簇的均值；

              Until      簇的质心不再变化。
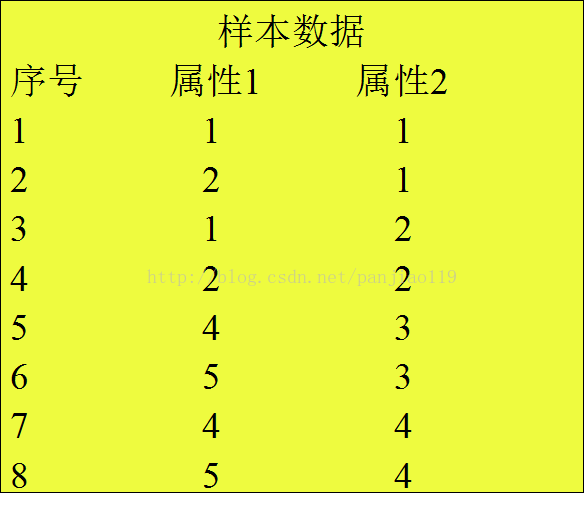
20   k-means例子

     步骤如下：

k-means(设n=8，k=2)步骤：
第一次迭代：假定随机选择的两个对象，如序号1和序号3当作初始点，分别找到离两点最近的对象，并产生两个簇{1，2}和{3，4，5，6，7，8}。对于产生的簇分别计算平均值，得到平均值点。对于{1，2}，平均值点为（1.5，1）（这里的平均值是简单的相加出2）；对于{3，4，5，6，7，8}，平均值点为（3.5，3）。
第二次迭代：通过平均值调整对象的所在的簇，重新聚类，即将所有点按离平均值点（1.5，1）、（3.5，1）最近的原则重新分配。得到两个新的簇：{1，2，3，4}和{5，6，7，8}。重新计算簇平均值点，得到新的平均值点为（1.5，1.5）和（4.5，3.5）。
第三次迭代：将所有点按离平均值点（1.5，1.5）和（4.5，3.5）最近的原则重新分配，调整对象，簇仍然为{1，2，3，4}和{5，6，7，8}，发现没有出现重新分配，而且准则函数收敛，程序结束。

迭代次数   平均值       平均值                       产生的新簇                    平均值         平均值
  （簇1）     （簇2）    （簇1）       （簇2）
 
   1 （1，1）     （1，2）           {1，2}，{3，4，5，6，7，8}    （1.5，1）  （3.5，3）
   2 （1.5，1）   （3.5，3）        {1，2，3，4}，{5，6，7，8}   （1.5，1.5）（4.5，3.5）        
   3 （1.5，1.5）（4.5，3.5）     {1，2，3，4}，{5，6，7，8}   （1.5，1.5）（4.5，3.5） 

21    ：

k-means算法特点
(1)优点：
在处理大数据集时，该算法是相对可扩展性的，并且具有较高的效率。
算法复杂度为O(nkt),其中，n为数据集中对象的数目，k为期望得到的簇的数目，t为迭代的次数。
(2)应用局限性：
用户必须事先指定聚类簇的个数；
常常终止于局部最优；
只适用于数值属性聚类(计算均值有意义)；
对噪声和异常数据也很敏感；
不适合用于发现非凸形状的聚类簇。

22   k-means算法改进工作

   算法改进：
①参数k的选择；②差异程度计算；③聚类均值的计算方法。
例如：
先应用自下而上层次算法来获得聚类数目，并发现初始分类，然后再应用循环再定位(k-mean)来帮助改进分类结果。
k-modes：用新的相异性度量方法处理对象，用基于频率的方法修改簇的modes。
k-prototype:将k-means扩展到处理符号属性。
EM(期望最大化)
    (1)  概率权值,聚类边界不严格
    (2)  可扩展性,识别数据中存在的三种类型区域

23  K-中心点算法：

   k-meams  和 k-medoids 比较

   k-means利用簇内点的均值或加权平均值ci（质心）作为簇Ci的代表点。对数值属性数据有较好的几何和统计意义。

     对孤立点是敏感的，如果具有极大值，就可能大幅度地扭曲数据的分布。
k-中心点(k-medoids)算法是为消除这种敏感性提出的，它选择簇中位置最接近簇中心的对象(称为中心点)作为簇的代表点，

24   k-中心点算法处理过程
首先，随机选择k个对象作为初始的k个簇的代表点，将其余对象按与代表点对象的距离分配到最近的簇；
然后，反复用非代表点来代替代表点，以改进聚类质量。(用一个代价函数来估计聚类质量，该函数度量对象与代表点对象之间的平均相异度。)

 目标函数仍然可以采用平方误差准则。

25

k-中心点算法
输入：n个对象的数据库，期望得到的k个聚类簇
输出：k个簇，使所有对象与其所属簇中心点的偏差总和最小化
方法：
    选择k个对象作为初始的簇中心
   repeat
        （1）将每个剩余的对象，分配到最近的中心点所代表的的簇；
        （2）随机选取非中心点Orandom；
        （3）计算用Orandom代替中心点Oj形成新聚类的总代价S；
        （4）If S<0 then用Orandom代替Oj，形成新的k个中心点的集合。
     until 不再发生变化

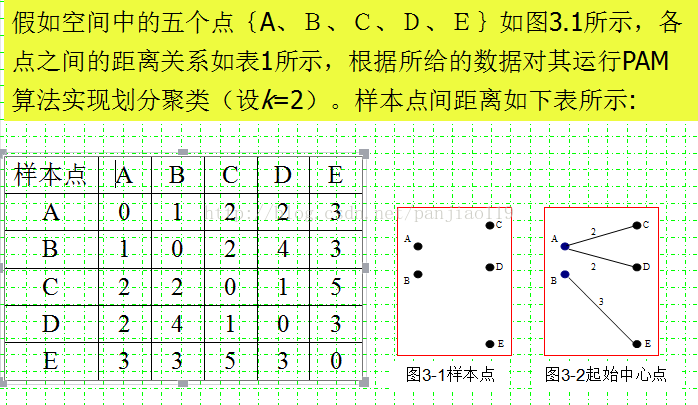
26 k-中心点算法例子

28  

      第一步建立阶段：
        假如从5个对象中随机抽取的2个中心点为{A，B},则样本被划分为{A、C、D}和{B、E}，如图3.2所示。
第二步交换阶段：
       假定中心点A、B分别被非中心点{C、D、E}替换，根据PAM算法需要计算下列代价TCAC、TCAD、TCAE、TCBC、TCBD、TCBE。

以TCAC为例说明计算过程：
a)当A被C替换以后，A不再是一个中心点，因为A离B比A离C近，A被分配到B中心点代表的簇，CAAC=d(A,B)-d(A,A)=1。
b)B是一个中心点，当A被C替换以后，B不受影响，CBAC=0。
c)C原先属于A中心点所在的簇，当A被C替换以后，C是新中心点，符合PAM算法代价函数的第二种情况CCAC=d(C,C)-d(C,A)=0-2=-2。
d)D原先属于A中心点所在的簇，当A被C替换以后，离D最近的中心点是C，根据PAM算法代价函数的第二种情况CDAC=d(D,C)-d(D,A)=1-2=-1。
e)E原先属于B中心点所在的簇，当A被C替换以后，离E最近的中心仍然是B，根据PAM算法代价函数的第三种情况CEAC=0。
因此，TCAC=CAAC+CBAC+CCAC+CDAC+CEAC=1+0-2-1+0=-2。

或者这样理解 ：

TC_ij表示用非中心点j替换中心点i所产生的代价。 
计算TC_AC：当A被C替换后，设一指针p遍历所有对象，判断他们是否聚到别的类里。

1. 先看A是否变化：C成为中心点后，A离B比A离C近，故A被划分到B簇里。所产生的代价为d(A,B)-d(A,A)=1(d(i,j)表示i划分到中心点j的距离；差值表示属于新的中心点-属于旧的中心点产生的代价。)
2. 看B是否变化：C成为中心点后，B当然离自己是最近的，不变
3. 看C是否变化：C成为中心点后，C划分到C簇里，代价为d(C,C)-d(C,A)=-2
4. 看D是否变化：C成为中心点后，D离C最近，故划分到C里，代价为d（D,C）-d（D,A）=-1；
5. 看E是否变化：C成为中心点后，E离B最近，为0 
   TC_AC就等于上述的代价之和，为1+0-2-1+0=-2。 
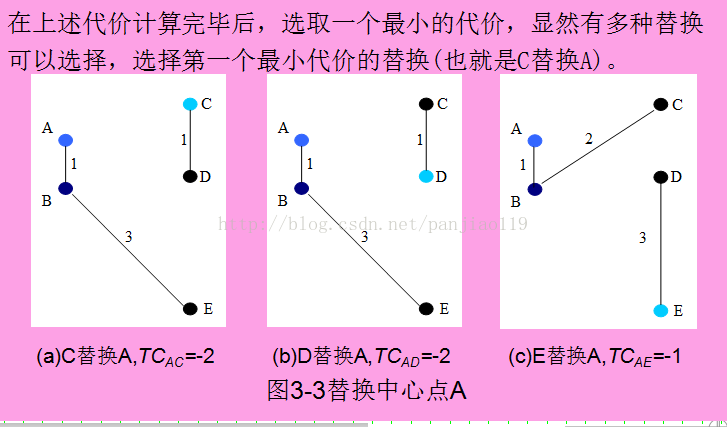
   同理需要计算TC_AD=-2、TC_AE=-1、TC_BC=-2、TC_BD=-2、TC_BE=-2 
   然后选取代价最小的替换，这里有多个选择，随便选择一个就行。选C的话，新的簇为{C,D}和{A,B,E}。新的簇中心为C，B，继续迭代计算直到收敛。

为了判定一个非代表对象o_random是否是当前一个代表对象o_{i的好的替代，对于每一个非中心点p，需要考虑下面4中情况：}

---

第一种情况：p当前隶属于代表对象o_j（A类中心点），如果o_j被o_random所代替作为代表对象，并且p离其他代表对象o_i（B类的中心点）最近，则p重新分配给o_i。(i!=j)

---

第二种情况：p当前隶属于代表对象o_j（A类中心点），如果o_j被o_random所代替作为代表对象，并且p离o_random（新的中心点）最近，则p重新分配给o_random。(i!=j)

---

第三种情况：p当前隶属于代表对象o_i（B类中心点），如果o_j被o_random所代替作为代表对象，并且p仍然离o_i最近，则p不发生变化。(i!=j)

---

第四种情况：p当前隶属于代表对象o_i（B类中心点），如果o_j被o_random所代替作为代表对象，并且p离o_random最近，则p重新分配给o_random。(i!=j)

29   K-中心点算法特点
(1)优点：
对属性类型没有局限性；
鲁棒性强：通过簇内主要点的位置来确定选择中心点，对孤立点和噪声数据的敏感性小。
(2)不足：
处理时间要比k-mean更长；
用户事先指定所需聚类簇个数k。

30  围绕中心点的划分(Partitioning Around Medoid，PAM)
最早提出的k-中心点算法之一；
总在中心点周围试图寻找更好的中心点；
针对各种组合计算代价；
不足在于n和k较大时，时间代价太大。