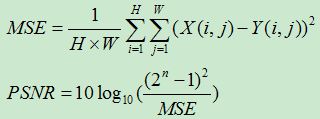图像增强算法效果评价指标及实现

前言：

对于一种图像处理方法，怎么样来判断该算法效果的好坏呢？除了人眼本身的观察，还可以用某种指标来量化评判，本文将总结一下图像质量评判的方法及实现。

图像质量评价分类（IQA:image quality assessment）：

图像质量评价目前来看主要分为两类：

（1）主观评价。即用人眼观察和评判图像，主观评价和人的感觉相一致，但是容易受到环境、心境等影响，而且大量评价图像时也显得不现实。

（2）客观评价。即采用算法进行评价，相比于主观评价，客观评价具有操作简单、成本低、易于解析和实现等优点，是图像质量评价的研究重点。所以本篇重点总结一下客观评价的几种方法。

客观评价算法根据其对参考图像的依赖程度， 可分成三类：( 1) 全参考: 和参考图像的所有像素点做对应比较; ( 2) 半参考: 只需要和参考图像上的部分统计特征做比较;( 3) 无参考: 不需要具体的参考图像。其中全参考算法是研究时间最长、发展最成熟的。

一、全参考评价：

全参考算法根据算法采用的技术路线， 可分为基于误差统计量的算法和基于 HVS 模型的算法。

1.基于误差统计量的算法的思路： 通过设计特征来比较失真图像和参考图像的局部差异, 然后在整幅图像上求出一个总的平均统计量, 并把这个统计量与图像质量关联起来。最简单的质量评价算法就是均方差(Mean Squared Error, MSE)和峰值信噪比(Peak Signal- Noise Ratio, PSNR)。MSE 和 PSNR 计算复杂度小，易于实现，在图像处理领域中广泛应用。但缺点是它们给出的数值与图像的感知质量之间没有必然联系。

2.基于 HVS 模型的算法的思路：通过对 HVS 的某些底层特性进行建模，将失真图像和参考图像之间的绝对误差映射为能被人眼觉察的 JND( Just noticeable difference) 单位。根据对 HVS 模型描述的侧重点不同，又可以将图像质量评价模型归结为基于误差灵敏度评价算法和基于结构相似度评价算法两类。

2.1基于误差灵敏度的质量评价算法

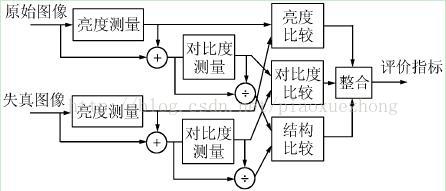
该方法可用图1描述，算法不同之处在于侧重点和处理方式上的区别。

图1.基于误差灵敏度的评价框架

该方法的缺点在于：

(a)基于 HVS 特征的方法一般认为原始图像质量是完美的，Weber 定律和点扩散函数(Point Spread Function)模型始终成立。

(b)一般假定 HVS 的多通道响应可以通过线性离散集合来模拟。

(c)一般假定通道分解是无损或无损于视觉的，变换后仍保持了质量评价的绝大部分信息。

(d)一般认为通道分解剔除了图像间的关联，道变换的作用可以通过掩蔽模型来模拟。

(e)HVS 的评价值可以通过测试误差的非线性组合来模拟，目前大多采用线性加权组合。

前 3 条假设从 HVS 的特点以及实际操作来说，相对比较合理。实验表明自然图像经过通道分解后，相同位置上的特征基本上相同或者相似，即各通道之间实际上存在较高的相关性，这与上述(d)点假设相矛盾。另外，误差的统计量来表征图像质量方法，论其如何加权组合，仍可能存在两幅图像失真类型完全不一样、但误差相同的现象。故上述(e)点假设也不合适。

2.2基于结构相似度的图像质量评价算法

自然图像具有特定的结构，素间有很强的从属关系，这些从属关系反映了视觉场景中的结构信息。由此产生了基于结构失真的图像质量评价方法，称为结构相似 (SSIM)方法，框架参见图2。

图2.结构相似度评价框架

小结：基于误差灵敏度的方法通过人为模拟 HVS 对误差敏感度进行量化，过程易于解析，但是其算法过于繁杂；SSIM 评价方法通过测量图像结构信息的改变来反映图像质量的失真情况，算法上明显简化，但同时也屏蔽掉了 HVS的其它生理特征，过程不易于解析。所以，将 SSIM 和基于误差灵敏度的评价方法中采用的 HVS 特征加权评价联合起来，是图像质量评价今后的一个发展方向。

二、半参考评价：

半参考算法可以分为两种: 基于图像特征统计量的算法和基于数字水印的算法。这类算法的特点是其只需从参考图像中提取部分统计量用于比较, 无需原始的像素级别的信息。

三、无参考评价：

无参考算法可以分为两种: 针对失真类型的算法和 基于机器学习的算法。这类方法的特点无需参考图像, 灵活性强。无参考算法的难点在于如何使评价结果尽量不受图像内容的影响。

衡量算法性能的定量指标：

图像质量评价算法应该具备以下特性:

( 1) 准确性：主观与客观评价值之间的差异较小;

( 2) 单调性: 客观评价值应随主观评价值的增减而增减;

( 3) 一致性: 算法在测试集上表现出的性能与其在训练集上表现的性能相近似。

图像质量评价算法实现：

这里附上几种图像质量评价指标的算法实现。

（1）峰值信噪比-PSNR（Peak Signal to Noise Ratio）

峰值信噪比（PSNR）经常用作图像压缩等领域信号重建质量的评价，常简单的方式是通过均方差（MSE）来定义：

MSE为当前图像 X 和参考图像 Y 的均方误差（Mean Square Error）。H、W 分别表示图像的高和宽；n为每像素的比特数，一般取8，即像素灰阶数为256。PSNR的单位是dB，数值越大表示失真越小。

    function pnsr_result = psnr(img_ref,img_in)       
        %   img_ref is a high reference quality image   
        %   img_in is the denoise image    
        %   pnsr_result is the PSNR of the denoise image    
        width = size(img_ref,2);    
        heigh = size(img_ref,1);    
        if( width ~= size(img_in,2) || heigh ~= size(img_in,1) )    
            disp('Please check whether the input image and reference image have same size');    
            return    
        end    
        [a,b]=size(img_ref);      
        XX=double(img_ref) - double(img_in);      
        mse_value = sum(sum( XX.^2 ))/(a*b);      
        pnsr_result = 10*log10( 255*255 / mse_value );   
    end

（2）SSIM

两张图像 X 和 Y 的结构相似性可按照以下方式求出:

,

其中 μ 是平均值，是的方差，σ是的方差，σxy是协方差。

，

是用来维持稳定的常数。L 是像素值的动态范围,k1=0.01,k2=0.03。结构相似性的范围为-1到1,当两张图像一模一样时，SSIM的值等于1。
结构相似度指数从图像组成的角度将结构信息定义为独立于亮度、对比度，反映场景中物体结构的属性，并将失真建模为亮度、对比度和结构三个不同因素的组合。均值作为亮度的估计，标准差作为对比度的估计，协方差作为结构相似程度的度量。

• matlab实现：http://download.csdn.net/download/piaoxuezhong/10043453
• C++实现：http://mehdi.rabah.free.fr/SSIM/
  

其中，matlab实现里附带了详细的步骤说明和测试函数，我这附下测试结果：

（3）信噪比（SNR）

顾名思义，信噪比就是有用信号与噪声信号的比值，具体我直接附维基里的定义：

matlab实现：

function snr=SNR2(I,In)
% 计算噪声比
% I :original signal
% In:noisy signal
% snr=10*log10(sigma2(I2)/sigma2(I2-I1))

[~,~,nchannel]=size(I);
snr=0;
I=double(I);
In=double(In);
if nchannel==1
    Ps=sum(sum((I-mean(mean(I))).^2));%signal power
    Pn=sum(sum((I-In).^2));%noise power
    snr=10*log10(Ps/Pn);
elseif nchannel==3
    for i=1:3
        Ps=sum(sum((I(:,:,i)-mean(mean(I(:,:,i)))).^2));%signal power
        Pn=sum(sum((I(:,:,i)-In(:,:,i)).^2));%noise power
        snr=snr+10*log10(Ps/Pn);
    end
    snr=snr/3;
end

测试函数结果：

%% snr
clc,clear all,close all;
ref = imread('D:\fcq_proMatlab\test_image\15.jpg');
H = fspecial('Gaussian',[11 11],1.5);
A = imfilter(ref,H,'replicate');
subplot(1,2,1); imshow(ref); title('Reference Image');
subplot(1,2,2); imshow(A);   title('Blurred Image');
snrValue=SNR2(ref,A )

snrValue =

   25.6430

参考：

1. 《图像质量评价研究综述》[J]. 计算机科学
2. 《图像质量研究方法进展》[J]. 电子与信息学报
3. 《基于频域的结构相似度的图像质量评价方法》[J]. 清华大学学报
4. http://blog.csdn.net/purgle/article/details/73719101
5. http://blog.csdn.net/ebowtang/article/details/43643037
6. http://blog.csdn.net/xiaohaijiejie/article/details/48053595