算法模型---算法调优---数据挖掘模型效果评估方法汇总
基于损失函数的标准
sklearn中的模型评估
混淆矩阵
混淆矩阵用在分类器中，是对每一类样本的统计，包括正确分类和错误分类的个数。对于m类样本，可能的错误种类有 m 2 − m m^2-m m2−m个。
对于2分类问题存在4种可能的情况：
| 实际的类 | ||||
| 预测的类 | c_+ | c_- | 合计 | |
| c_+ | TurePositive | FalseNegative | Actual Positive=TP+FN | |
| c_- | FalsePositive | TureNegative | Actual Negative=FP+TN | |
| 总计 | Predicted Positive=TP+FP | Predicted Negative=FN+TN | TP+FP+FN+TN | |
多分类问题类似，只是情况更多。
准确率及误差率的度量
为了度量预测的精确度，隐含假设每一个错误分类的样本成本相同，引入误差率和准确率两个指标作为这种成本的度量。
误差率： 错误分类的样本数(E)与检测样本总数(S)的比值
R = E / S R=E/S R=E/S
准确率： 正确分类的样本数与检测样本总数(S)的比值
A = 1 − R = S − E S A=1-R=\frac{S-E}{S} A=1−R=SS−E
我们也可以引入更全面的指标：
用 p o s pos pos表示真实正例的样本数， n e g neg neg表示真实负例的样本数， T P TP TP表示正确预测的正例样本数， F P FP FP表示负例被当成正例的样本数， T N TN TN表示正确预测的负例样本数， F N FN FN表示正例被当成负例的样本数。以下括号中的文字有些是自己给取的名字，不要跟其他地方混淆了。
灵敏度(真正率)： 在预测的正例里有多少是真正的（比例）（有点查全的感觉，真的有这么多正例，有多少被挑出来了）
T r u e P o s i t i v e R a t e = S e n s i t i v i t y = T P T P + F N True\ Positive\ Rate=Sensitivity=\frac{TP}{TP+FN} True Positive Rate=Sensitivity=TP+FNTP
即召回率(查全率Recall)： 计算方法同真正率，相同东西在不同场合下的叫法。
特异性（真负率）： 在预测的负例里有多少是正负的（比例）（有点查全的感觉，只不过是会对负例样本，真的有这么多负例，有多少被挑出来了）
S p e c i f i c i t y = T N T N + F P Specificity=\frac{TN}{TN+FP} Specificity=TN+FPTN
精度（查准率）： 即在预测结果的正例里真实正例的比例（有点查准的感觉，预测了这么多，多少预测对了）
P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP
即查准率Precision)： 与精度计算方法相同
错误正例(假正率)： 在预测的正例里有多少是假的（比例）
F a l s e P o s i t i v e R a t e = 1 − T N T N + F P = F P T N + F P False\ Positive\ Rate=1-\frac{TN}{TN+FP}=\frac{FP}{TN+FP} False Positive Rate=1−TN+FPTN=TN+FPFP，
错误负例(假负率)： 在预测的负例里有多少是正的（比例）
F a l s e N e g e t i v e R a t e = 1 − T P T P + F N = F N T P + F N False\ Negetive\ Rate=1-\frac{TP}{TP+FN}=\frac{FN}{TP+FN} False Negetive Rate=1−TP+FNTP=TP+FNFN
可重新表达：准确率:
A = T P + T N p o s + n e g = T P p o s ∗ p o s p o s + n e g + T N n e g n e g p o s + n e g A=\frac{TP+TN}{pos+neg}=\frac{TP}{pos}*\frac{pos}{pos+neg}+\frac{TN}{neg}\frac{neg}{pos+neg} A=pos+negTP+TN=posTP∗pos+negpos+negTNpos+negneg
上面的概念中只要记住真正率的概念，真负率与之相似，都是表达在预测的XX里，真的XX的占比；而假正率和假负率又分别与前面的真正率和真负率互补，都是1-XX比例，或者说都是在表达在预测的XX里，假的XX的占比；召回率（查全率）这个很好理解，我们分析数据的目的一般就是 奔着正例去的，能找出来越多越好，其表达式与真正率一样也就好理解；查准率也较好理解，有一个准字在表达式里，说明和准确率有关，同样它也是奔着正例去，在预测的正例里预测对了多少，与之相似的是准确率，准确率是针对全体样本，不管正负看总体预测对了多少。
最终
F_1值：
F 1 = 2 ∗ P ∗ R P + R F_1=\frac{2*P*R}{P+R} F1=P+R2∗P∗R，更一般的形式为 F 1 = ( 1 + β 2 ) P ∗ R ( β 2 ∗ P ) + R F_1=\frac{(1+\beta^2)P*R}{(\beta^2*P)+R} F1=(β2∗P)+R(1+β2)P∗R这里的P指查准率，R指查全率
β=1退化为F1；β>1查全率有更大影响；β<1查准率有更大影响。
宏平均（macro-average）: 一般用在文本分类器，是先对每一个类统计指标值，然后在对所有类求算术平均值。宏平均指标相对微平均指标而言受小类别的影响更大。
微平均（micro-average）： 一般用在文本分类器，是对数据集中的每一个实例不分类别进行统计建立全局混淆矩阵，然后计算相应指标。
平均准确率(Average Per-class Accuracy): 为了应对每个类别下样本的个数不一样的情况，计算每个类别下的准确率，然后再计算它们的平均值。
对数损失函数(Log-loss): 在分类输出中，若输出不再是0-1，而是实数值，即属于每个类别的概率，那么可以使用Log-loss对分类结果进行评价。这个输出概率表示该记录所属的其对应的类别的置信度。比如如果样本本属于类别0，但是分类器则输出其属于类别1的概率为0.51，那么这种情况认为分类器出错了。该概率接近了分类器的分类的边界概率0.5。Log-loss是一个软的分类准确率度量方法，使用概率来表示其所属的类别的置信度。对数损失函数越小，模型就越好。可参考：对数损失函数(Logarithmic Loss Function)的原理和 Python 实现
评价模型成本的可视化工具
machine learning week6 诊断机器学习算法的性能 各种学习曲线 来判断学习算法是过拟合或欠拟合
Model evaluation: quantifying the quality of predictions
论XGBOOST科学调参
深度探讨机器学习中的ROC和PR曲线
机器学习性能指标之ROC和AUC理解与曲线绘制
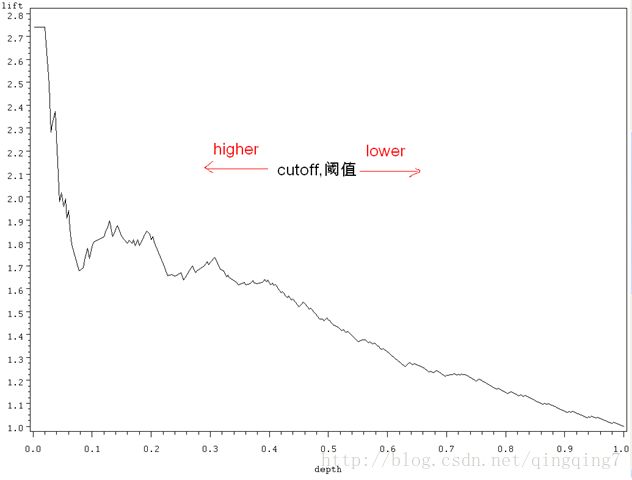
lift图
lift 叫提升指数，也就是运用模型比不运用模型精度的提升倍数。
l i f t = T P T P + F P / T P + F N T P + F N + F P + T N lift=\frac{TP}{TP+FP}/\frac{TP+FN}{TP+FN+FP+TN} lift=TP+FPTP/TP+FN+FP+TNTP+FN
也可以表示为
l i f t = 累 计 预 测 精 度 平 均 精 度 lift=\frac{累计预测精度}{平均精度} lift=平均精度累计预测精度
结论是：提升指数越高，模型的准确率越高。
对准确率进行提升的例子：
假设根据以往的经验，问卷调查的回应率为20%，即发出100份问卷收回的有20份，但是通过对历史数据的分析发现特定人群的回应率会更高（数据分析的过程即为建模），然后对特定人群进行发放整个回应率就得到提升。
用在数据挖掘模型里也是一样，利用模型能对准确率提升越多，单方面来讲模型效果就越好。
具体做法如下：
I、 计算出测试样本中正例的百分比，即为平均精度；
II、 利用模型对测试样本进行预测，按预测得分降序将样本排序，将排序好的样本分成10份，即按10分位数操作；
III、 计算第1份样本中的预测精度，然后利用预测精度/平均精度，得到第1份数据的提升指数；
IV、 计算至第2份样本处的累计预测精度，然后利用累计预测精度/平均精度，得到至第2份样本处的提升指数；
VI、 依次得到10个节点处的提升指数；
VI、 画出基线（各节点处均为1）及不同模型提升指数的曲线图；
VII、 进行模型效果对比，图形越高越好；
ROC曲线
ROC曲线是利用真正率为纵轴，假正率为横轴画出的曲线，用来评估模型预测准确率。很明显，当真正率大越近1，假正率越接近0是模型越好。
对于给定的一组样本，我们只能得到一个真正率和一个假正率（对应图上的一个点），那如何画ROC曲线呢？
假设采用逻辑回归分类器，其给出针对每个实例为正类的概率，那么通过设定一个阈值如0.6，概率大于等于0.6的为正类，小于0.6的为负类。对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点。不同的阈值可以得到不同点。随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着真正的负实例，即TPR和FPR会同时增大。阈值最大时，对应坐标点为(0,0),阈值最小时，对应坐标点(1,1)。所有这些点连起来即得到了ROC曲线；
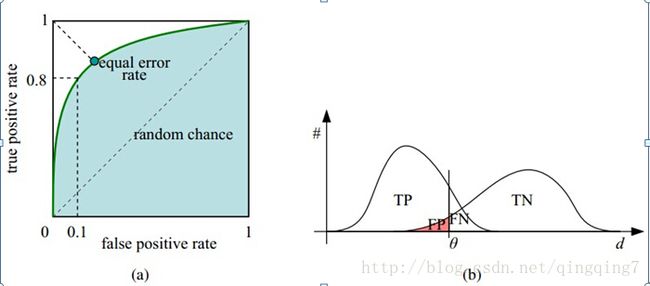
真正率大越近1，假正率越接近0是模型越好，在图上的表现就是ROC曲线越靠近(0,1)点，越远离 4 5 o 45^o 45o对角线；
评价模型有很多指标，为什么还要使用ROC和AUC呢？因为ROC曲线有个很好的特性：当测试集中的正负样本的分布变换的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现样本类不平衡，即正负样本比例差距较大，而且测试数据中的正负样本也可能随着时间变化。
ROC曲线在概念上和PR曲线类似,它是对分类器的真阳性率假阳性率的图形化解释。
真阳性率(TPR)是真阳性的样本数除以真阳性和假阴性的样本数之和。换句话说,TPR是 真阳性数目占所有正样本的比例。这和之前提到的召回率类似,通常也称为敏感度。
假阳性率(FPR)是假阳性的样本数除以假阳性和真阴性的样本数之和。换句话说,FPR是 假阳性样本数占所有负样本总数的比例。
通过来讲，对同一个数据分析任务，数据集相同，我们可以看一个ROC曲线是否包含另一个，被包含的那个较差，如果两者相关交，就要看曲线下面积，比较麻烦，此时可以看f1得分等；但不同的数据分析任务，ROC就放在一起比较就没有什么意义。
如何画roc曲线
机器学习性能指标之ROC和AUC理解与曲线绘制
AUC曲线
AUC(area under curve): 即ROC曲线下的面积。
若一个学习器的ROC曲线被另一个包住，后者的性能能优于前者；若交叉，判断ROC曲线下的面积，即AUC。
关于AUC的计算方法，可参考AUC计算方法总结
在考查AUC时也要考查其他指标AUC越大，正确率就越高？
PR曲线
坐标为查准率，横坐标为召回率真
如何画PR曲线
与roc曲线的画法类似
areaUnderPR
这里的PR指查准率和查全率 .
通常,准确率和召回率是负相关的,高准确率常常对应低召回率,反之亦然。为了说明这点, 假定我们训练了一个模型的预测输出永远是类别1。因为总是预测输出类别1,所以模型预测结果 不会出现假阴性,这样也不会错过任何类别1的样本。于是,得到模型的召回率是1.0。另一方面, 假阳性会非常高,意味着准确率非常低(这依赖各个类别在数据集中确切的分布情况)。
准确率和召回率在单独度量时用处不大,但是它们通常会被一起组成聚合或者平均度量(比如f1得分)。二 者同时也依赖于模型中选择的阈值。
直觉上来讲,当阈值低于某个程度,模型的预测结果永远会是类别1。因此,模型的召回率 为1,但是准确率很可能很低。相反,当阈值足够大,模型的预测结果永远会是类别0。此时,模 型的召回率为0,但是因为模型不能预测任何真阳性的样本,很可能会有很多的假阴性样本。不 仅如此,因为这种情况下真阳性和假阳性为0,所以无法定义模型的准确率。
准确率-召回率(PR)曲线,表示给定模型随着决策阈值的改变,准确率和召回 率的对应关系。PR曲线下的面积为平均准确率。直觉上,PR曲线下的面积为1等价于一个完美模 型,其准确率和召回率达到100%。
当正负样本差距不大的情况下，ROC和PR的趋势是差不多的，但是当负样本很多的时候，两者就截然不同了，ROC效果依然看似很好，但是PR上反映 效果一般。解释起来也简单，假设就1个正例，100个负例，那么基本上TPR可能一直维持在100左右，然后突然降到0.
areaUnderPR和AUC更详细的情况可查看，ROC曲线和PR曲线。两者的分子分母都不一样
偏差和方差
机器学习中的PR曲线和ROC曲线
机器学习算法笔记之9：偏差与方差、学习曲线
泛化误差可以分解为偏差、方差与噪声之和
偏差度量了学习算法的期望预测和真实结果偏离程度。
方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。
噪声可以认为数据自身的波动性，表达了目前任何学习算法所能达到泛化误差的下限。
偏差大说明欠拟合，方差大说明过拟合。
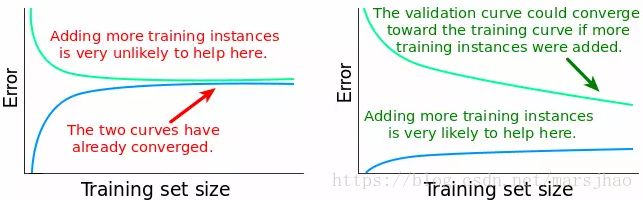由上图左图可以得到，当训练集样本数增大到某个值以后时，验证集的误差保持大致不变，表明增加更多的训练数据点并不能带来更好的模型，与其增大训练集的规模，不如尝试构建更加复杂的模型算法。而右图则表明增加更多训练样本会降低模型误差，改善模型性能。
高验证集误差表明是一个偏差问题，但并不能直接指明具体的偏差问题。与此同时，高训练集误差表明是高偏差问题（欠拟合），模型不能很好地拟合训练数据；而低训练集误差表明是低偏差问题，模型可以很好地拟合训练数据。
方差variance问题诊断：首先检查验证学习曲线和训练学习曲线之间的差距，然后检查训练误差（检查误差值随训练样本数的增加的变化）。
两曲线较小的差距代表较小的variance，差距越小则variance越小，反之亦然。高方差即variance较大说明出现了过拟合问题（过度拟合训练数据）。当过拟合的模型分别在训练集和验证集上测试时，训练误差较低而验证误差较高，且随着训练样本数的增加这种模式继续存在，训练集和验证集之间的差异程度决定了这两条曲线之间的距离。
训练误差和验证误差之间的关系，以及训练学习曲线和验证学习曲线之间的差距可以总结如下：gap = validation_error − training_error。两个误差之间的差距越大，曲线之间的距离越大，variance 越大。
通常，以下两种修正方式在处理高 bias 和低 variance 的问题时会比较奏效：
用更多的特征训练当前的学习算法，即通过增加模型的复杂度来降低 bias。
减少对当前算法的正则化。正则化能够避免算法在训练数据上过拟合。如果我们减少了正则化，模型会更好地拟合训练数据，就会增加 variance，降低 bias。
理想化的学习曲线应该是两条学习曲线都收敛至误差为0的时候，而实际上这是不可能的
sklearn 中的学习曲线应用
from sklearn.model_selection import learning_curve
评估分类器的准确率
上面讲的评价模型的指标或曲线都是在测试集中进行的，也就是我们需要将数据集分为训练集和测试集，训练集用于训练模型参数，测试集用于检验模型在数据中的预测效果。这就是我们评估分类器大的方法。下面介绍将数据划分为训练集和测试集的方法。
再替换方法
所有的数据即用于训练模型也用于检验模型
保持方法和随机子抽样
保持方法(hold out)： 按一定比例随机地从数据集中抽取一部分样本作训练集，剩下的样本为测试集，通训练集在2/3~4/5之间；
随机子抽样(random subsampling)： 抽取一定比例样本做为训练集，剩下的样本为测试集；然后在第1次的训练集重复该操作；重复n次，评论指标的平均值作为最终的评价值；这是一种无放回抽样；
交叉验证法
K折交叉验证(K-fold cross-validation): 将样本分成K份，每份数量大致相等，然后用其他的某一份作为测试，其他样本作为训练集，得到一个模型和一组预测值及模型评估值；循环这个过程K次，得到K组模型评估值，对其取平均值即得到最终的评估结果；
留一(leave-one-out): 是K-fold cross-validation的特征形式，每次只取一个样本作为测试样本，其余样本作为训练样本，重复该过程K次（假如样本总数为K）。
自助法
自助法(bootstrap method): 在数据集中采用有放回的方式抽样，产生训练集和测试集；重复该过程n次。
基于统计检验的标准
统计模型之间的距离
距离是典型的相似性指标。
欧氏距离
熵距离
卡方距离
0-1距离
我并不认为用距离评估模型的效果是一种好的做法，只有不同类样本在样本内扎堆，类间分离的时候这种检测才是一致的。
统计模型的离差
离差即误差的统称：如标准差，方差都为这一类
欧氏离差即为平均误差和。
基于记分函数的标准
贝叶斯标准
计算标准
交叉检验标准
利用交叉检验的处理方法，再配合其他指标如离差进行检验。
自展标准
遗传算法
其他评价指标
计算速度： 分类器训练和预测需要的时间；
鲁棒性： 处理缺失值和异常值的能力；
可扩展性： 处理大数据集的能力；
可解释性： 分类器的预测标准的可理解性，像决策树产生的规则就是很容易理解的，而神经网络的一堆参数就不好理解，我们只好把它看成一个黑盒子。
回归模型评估指标
RMSE（root mean square error，平方根误差）： 其又被称为RMSD（root mean square deviation），RMSE对异常点（outliers）较敏感，如果回归器对某个点的回归值很不理性，那么它的误差则较大，从而会对RMSE的值有较大影响，即平均值是非鲁棒的。其定义如下：
MAE（ mean absolute error，平均绝对误差）：
Quantiles of Errors： 为了改进RMSE的缺点，提高评价指标的鲁棒性，使用误差的分位数来代替，如中位数来代替平均数。假设100个数，最大的数再怎么改变，中位数也不会变，因此其对异常点具有鲁棒性。
判定系数（coefficient of determination，记为 R 2 R^2 R2或 r 2 r^2 r2）: 用于度量因变量的变异中可由自变量解释部分所占的比例，以此来判断统计模型的解释力。
sklearn中的评价函数
http://scikit-learn.org/stable/modules/classes.html#sklearn-metrics-metrics
分类主要是基于混淆矩阵，回归主要是基于误差。
sklearn.metrics.f1_score
sklearn中 F1-micro 与 F1-macro区别和计算原理
区别是micro是对所有样本求f1 score而macro是先在组内先求f1 scroe，然后对这些f1 scroe求加权平均；
y_true = [1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4]
y_pred = [1, 1, 1, 0, 0, 2, 2, 3, 3, 3, 4, 3, 4, 3]
print(f1_score(y_true,y_pred,labels=[1,2,3,4],average='micro'))
#>>> 0.615384615385
如果采用交叉验证，可以如下设置,可以看到它对每一组测试样本都会计算一个f1_score，我们可以简单采用这些f1_score的平均值来综合衡量模型的好坏，从而指导我们调参。
>> from sklearn import metrics
>>> scores = cross_val_score(
... clf, iris.data, iris.target, cv=5, scoring='f1_macro')
>>> scores
array([ 0.96..., 1. ..., 0.96..., 0.96..., 1. ])
聚类中的评估标准
聚类︱python实现 六大 分群质量评估指标（兰德系数、互信息、轮廓系数）
如何理解K-L散度（相对熵）
spark中的评估
Spark机器学习4·分类模型(spark-shell)