哈夫曼树C++实现

哈夫曼树的介绍

Huffman Tree，中文名是哈夫曼树或霍夫曼树，它是最优二叉树。

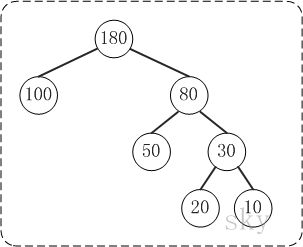
定义：给定n个权值作为n个叶子结点，构造一棵二叉树，若树的带权路径长度达到最小，则这棵树被称为哈夫曼树。 这个定义里面涉及到了几个陌生的概念，下面就是一颗哈夫曼树，我们来看图解答。

(01) 路径和路径长度

定义：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。 
例子：100和80的路径长度是1，50和30的路径长度是2，20和10的路径长度是3。

(02) 结点的权及带权路径长度

定义：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。 
例子：节点20的路径长度是3，它的带权路径长度= 路径长度 * 权 = 3 * 20 = 60。

(03) 树的带权路径长度

定义：树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL。 
例子：示例中，树的WPL= 1*100 + 2*50 + 3*20 + 3*10 = 100 + 160 + 60 + 30 = 290。

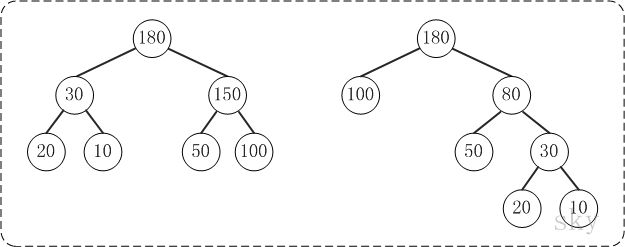
上面的两棵树都是以{10, 20, 50, 100}为叶子节点的树。

左边的树WPL=2*10 + 2*20 + 2*50 + 2*100 = 360 
右边的树WPL=350

左边的树WPL > 右边的树的WPL。你也可以计算除上面两种示例之外的情况，但实际上右边的树就是{10,20,50,100}对应的哈夫曼树。至此，应该堆哈夫曼树的概念有了一定的了解了，下面看看如何去构造一棵哈夫曼树。

哈夫曼树的图文解析

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，哈夫曼树的构造规则为： 

1. 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)； 
2. 在森林中选出根结点的权值最小的两棵树进行合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和； 
3. 从森林中删除选取的两棵树，并将新树加入森林； 
4. 重复(02)、(03)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。 
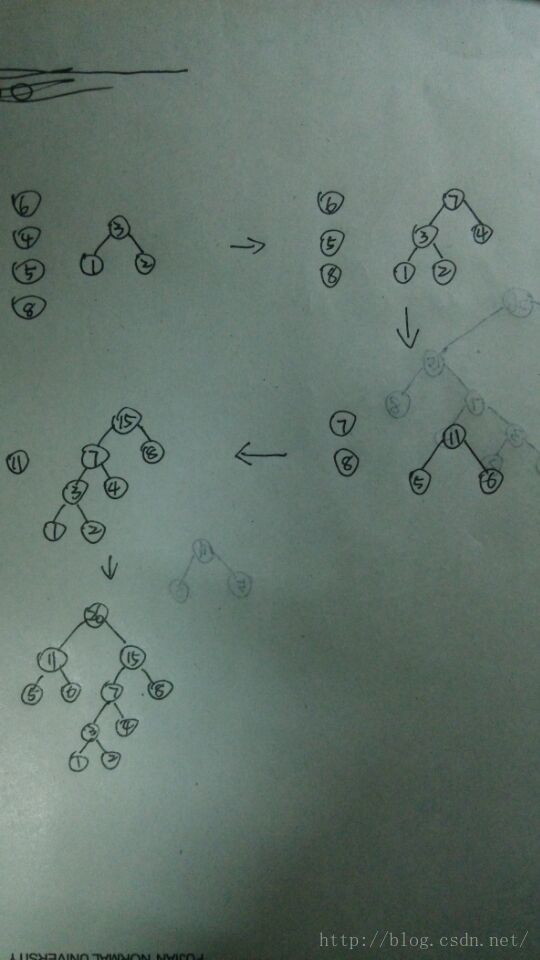
以{5,6,7,8,15}为例，来构造一棵哈夫曼树。

第1步：创建森林，森林包括5棵树，这5棵树的权值分别是5,6,7,8,15。 
第2步：在森林中，选择根节点权值最小的两棵树(5和6)来进行合并，将它们作为一颗新树的左右孩子(谁左谁右无关紧要，这里，我们选择较小的作为左孩子)，并且新树的权值是左右孩子的权值之和。即，新树的权值是11。 然后，将"树5"和"树6"从森林中删除，并将新的树(树11)添加到森林中。 
第3步：在森林中，选择根节点权值最小的两棵树(7和8)来进行合并。得到的新树的权值是15。 然后，将"树7"和"树8"从森林中删除，并将新的树(树15)添加到森林中。 
第4步：在森林中，选择根节点权值最小的两棵树(11和15)来进行合并。得到的新树的权值是26。 然后，将"树11"和"树15"从森林中删除，并将新的树(树26)添加到森林中。 
第5步：在森林中，选择根节点权值最小的两棵树(15和26)来进行合并。得到的新树的权值是41。 然后，将"树15"和"树26"从森林中删除，并将新的树(树41)添加到森林中。 
 此时，森林中只有一棵树(树41)。这棵树就是我们需要的哈夫曼树！ 

哈夫曼树的重点是如何构造哈夫曼树。构造哈夫曼时，用到了以前介绍过的"(二叉堆)最小堆"。

-PQ.h(prority_queue)优先队列

#ifndef __PQ_H__
#define __PQ_H__

#include 

template  >
class PQ {
private:
	T* data;
	size_t last;
	size_t maxSize;
	Compare isLessThan;

public:
	PQ(size_t sz = 20);
	~PQ();
	void destroy();
	T top()const;
	void pop();
	void push(const T& x);
	bool empty()const { return 0 == last; }
	void create(T* a, size_t sz);

private:
	void swim(size_t i);
	void sink(size_t i);
	void reSize();
};

template 
PQ::PQ(size_t sz) {
	last = 0;
	maxSize = sz + 1;
	data = new T[maxSize];
}

template 
PQ::~PQ() {
	destroy();
}

template 
void PQ::destroy() {
	last = 0;
	maxSize = 0;
	delete[] data;
}

template 
void PQ::swim(size_t i) {
	while (i > 1) {
		if (isLessThan(data[i / 2], data[i])) {
			std::swap(data[i / 2], data[i]);
			i /= 2;
		}
		else
			break;
	}
}

template 
void PQ::sink(size_t i) {
	while (i * 2 <= last) {
		int son = i * 2;
		if (son != last && isLessThan(data[son], data[son + 1]))
			son += 1;
		if (isLessThan(data[i], data[son])) {
			std::swap(data[i], data[son]);
			i = son;
		}
		else 
			break;
	}
}

template 
T PQ::top()const {
	return data[1];
}

template 
void PQ::pop() {
	data[1] = data[last--];
	sink(1);
}

template 
void PQ::push(const T& x) {
	if (last == maxSize - 1)
		reSize();
	data[++last] = x;
	swim(last);
}

template 
void PQ::reSize() {
	T* newData = new T[maxSize + maxSize / 2];
	for (size_t i = 0; i <= last; ++i)
		newData[i] = data[i];
	maxSize += maxSize / 2;
	delete[] data;
	data = newData;
}

template 
void PQ::create(T* a, size_t sz) {
	for (int i = 0; i < sz; ++i)
		push(a[i]);
}


#endif

-HuffmanTree.h

#ifndef __HUFFMAN_TREE_H__
#define __HUFFMAN_TREE_H__

#include 
#include "PQ.h"

template 
struct HuffmanNode {
	T key;
	HuffmanNode* parent;
	HuffmanNode* left;
	HuffmanNode* right;

	HuffmanNode(T value, HuffmanNode* p = NULL, 
		HuffmanNode* lt = NULL, HuffmanNode* rt = NULL)
		:key(value), parent(p), left(lt), right(rt) {}
};

// 自定义的仿函数，用来比较两个节点大小
template 
class HuffmanCmp {
public:
	bool operator()(HuffmanNode* lhs, HuffmanNode* rhs) {
		return lhs->key > rhs->key;
	}
};

template  >
class HuffmanTree {
private:
	HuffmanNode*		root;
	Compare				isLessThan;

public:
	HuffmanTree();
	~HuffmanTree();

	void preOrder()const;
	void inOrder()const;
	void postOrder()const;
	void print()const;

	void create(T* a, int size);
	void destroy();
	
private:
	void preOrder(HuffmanNode* node)const;
	void inOrder(HuffmanNode* node)const;
	void postOrder(HuffmanNode* node)const;
	void print(HuffmanNode* node, const T& key, const int& direction)const;

	void destroy(HuffmanNode*& node);

};

// constructor
template 
HuffmanTree::HuffmanTree() : root(NULL) {

}

// destructor
template 
HuffmanTree::~HuffmanTree() {
	destroy();
}

// destory
template 
void HuffmanTree::destroy() {
	destroy(root);
}

// Internal method: destroy
template 
void HuffmanTree::destroy(HuffmanNode*& node) {
	if (NULL == node) return;
	destroy(node->left);
	destroy(node->right);
	delete node;
}

/**
 * create
 * 一开始以数组的值构造一片只有一个节点的森林
 * 以Compare为比较函数，每次从堆中取出最小的树作为左子树
 *     再取出堆中最小的树作为右子树，构成一棵新的树，然后将新树放入heap中
 * 如此循环直到构建完成
 */
template 
void HuffmanTree::create(T* a, int size) {

	HuffmanNode *left, *right, *parent;
	PQ*, Compare> heap;

	for (int i = 0; i < size; ++i) {
		HuffmanNode* node = new HuffmanNode(a[i]);
		heap.push(node);
	}

	for (int i = 0; i < size - 1; ++i) {

		left = heap.top();
		heap.pop();
		right = heap.top();
		heap.pop();

		// 新建parent节点
		parent = new HuffmanNode(left->key + right->key, NULL, left, right);
		left->parent = right->parent = parent;

		heap.push(parent);
	}

	root = parent;
}

// print
template 
void HuffmanTree::print()const {
	print(root, T(), 0);
}

// Internal method: print
template 
void HuffmanTree::print(HuffmanNode* node, const T& key, const int& direction)const {
	
	if (NULL == node) return;

	if (node == root)
		std::cout << node->key << " is the root" << std::endl;
	else
		std::cout << node->key << " is " << key << "'s " 
		<< (direction == 1 ? "left" : "right") << " son" << std::endl;
	
	print(node->left, node->key, 1);
	print(node->right, node->key, 2);
}


#endif

-测试 main.cpp

#include "HuffmanTree.h"
#include "PQ.h"
#include 
#include 
using namespace std;

int main()
{
	HuffmanTree* ptree = new HuffmanTree;

	int a[] = { 6, 2, 4, 1, 5, 8 };

	ptree->create(a, 6);

	ptree->print();

	ptree->destroy();

	return 0;
}

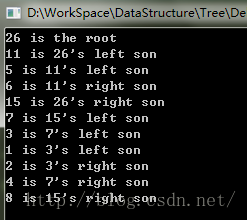
一开始的文字和图片介绍来自博客：http://www.cnblogs.com/skywang12345/p/3706821.html