数独相关题目汇总-Sudoku
Valid Sudoku数独定义:
1.每一行有九个1-9不同数字
2.每一列也有九个1-9不同数字
3.每九个方格也有九个1-9不同数字
1.判断数独是否有效-
描述
Determine if a Sudoku is valid, according to: Sudoku Puzzles - The Rules
The Sudoku board could be partially filled, where empty cells are filled with the character '.'
时间复杂度O(9^2),空间复杂度O(1)
// 1.判断数独是否有效
public static boolean isValidSudoku(char[][] matrix) {
boolean[] used = new boolean[9];
for (int i = 0; i < 9; i++) {
Arrays.fill(used, false);
for (int j = 0; j < 9; j++) {// 检查行
if (!check(matrix[i][j], used)) {
return false;
}
}
Arrays.fill(used, false);
for (int j = 0; j < 9; ++j) // 检查列
if (!check(matrix[j][i], used))
return false;
}
for (int r = 0; r < 3; r++) {
for (int c = 0; c < 3; c++) {
Arrays.fill(used, false);
for (int i = 3 * r; i < 3 * r + 3; i++) {
for (int j = 3 * c; j < 3 * c + 3; j++) {
if (!check(matrix[i][j], used)) {
return false;
}
}
}
}
}
return true;
}
public static boolean check(char tar, boolean[] used) {
if (tar == '.') {
return true;
}
if (used[tar - '1']) {
return false;
}
return used[tar - '1'] = true;
}2.填充单元完成数独-Sudoku Solver
描述
Write a program to solve a Sudoku puzzle by filling the empty cells.
Empty cells are indicated by the character '.' .
You may assume that there will be only one unique solution
// 2.填充单元完成数独,时间复杂度O(9^4),空间复杂度O(1)
public static boolean solveSodoku(char[][] matrix) {
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (matrix[i][j] == '.') {
for (int k = 1; k <= 9; k++) {
matrix[i][j] = Character.forDigit(k, 10);
if (isValid(matrix, i, j) && solveSodoku(matrix)) {
return true;
}
matrix[i][j] = '.';
}
return false;
}
}
}
return true;
}
// 检查 (x, y) 是否合法
public static boolean isValid(char[][] matrix, int x, int y) {
int i, j;
for (i = 0; i < 9; i++) // 检查 y 列
if (i != x && matrix[i][y] == matrix[x][y])
return false;
for (j = 0; j < 9; j++) // 检查 x 行
if (j != y && matrix[x][j] == matrix[x][y])
return false;
for (i = 3 * (x / 3); i < 3 * (x / 3 + 1); i++)
for (j = 3 * (y / 3); j < 3 * (y / 3 + 1); j++)
if ((i != x || j != y) && matrix[i][j] == matrix[x][y])
return false;
return true;
}
测试程序:
public static void main(String[] args) {
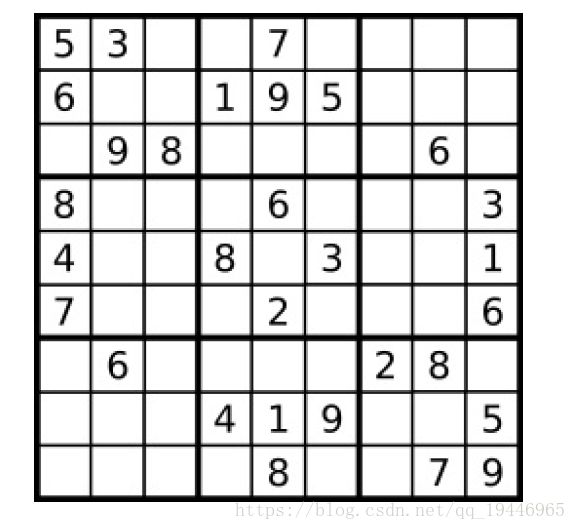
char[][] matrix = new char[][] { { '5', '3', '.', '.', '7', '.', '.', '.', '.' },
{ '6', '.', '.', '1', '9', '5', '.', '.', '.' }, { '.', '9', '8', '.', '.', '.', '.', '6', '.' },
{ '8', '.', '.', '.', '6', '.', '.', '.', '3' }, { '4', '.', '.', '8', '.', '3', '.', '.', '1' },
{ '7', '.', '.', '.', '2', '.', '.', '.', '6' }, { '.', '6', '.', '.', '.', '.', '2', '8', '.' },
{ '.', '.', '.', '4', '1', '9', '.', '.', '5' }, { '.', '.', '.', '.', '8', '.', '.', '7', '9' } };
System.out.println(isValidSudoku(matrix));
solveSodoku(matrix);
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[0].length; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}