视觉slam14讲——第5讲 相机与图像

本系列文章是记录学习高翔所著《视觉slam14讲》的内容总结，文中的主要文字和代码、图片都是引用自课本和高翔博士的博客。代码运行效果是在自己电脑上实际运行得出。手动记录主要是为了深入理解

第5讲 相机与图像

1 相机模型

相机模型是用来描述将三维世界坐标系中的坐标点映射到二维图像平面的过程
使用针孔和畸变两个模型来描述整个投影过程。

1.1 针孔相机模型

(1) 相机坐标系内中物理坐标点$\widetilde{P_c}=[X,Y,Z{]}^T$,
(2) 成像平面内成像坐标点$P^{{}^{\prime }}=[X^{{}^{\prime }},Y^{{}^{\prime }},Z^{{}^{\prime }}{]}^T$, 焦距为$f$,
通过对称成像平面和归一化成像平面得到二者关系为
$$\begin{gathered} X^{{}^{\prime }}=f\frac{X}{Z} \\ {Y}^{{}^{\prime }}=f\frac{Y}{Z} \end{gathered}$$
(3) 像素坐标系内像素坐标为$[u,v{]}^T$，像素坐标系和成像平面相差了一个缩放($u轴缩放\alpha 倍，v轴缩放\beta 倍$)和一个原点的平移$[c_x,c_y{]}^T$
$p^{{}^{\prime }}$和像素坐标$[u,v{]}^T$关系为
$$\begin{gathered} u=\alpha X^{{}^{\prime }}+c_x \\ v=\beta Y^{{}^{\prime }}+c_y \end{gathered}$$
代入上式得到像素坐标和相机坐标系内点的关系，
$$\begin{gathered} u=f_x\frac{X}{Z}+c_x \\ v=f_y\frac{Y}{Z}+c_y \end{gathered}$$
其中，$$f_x=\alpha f,f_y=\beta f$$
齐次化写成矩阵形式，
$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\frac{1}{Z}\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]=\frac{1}{Z}K\widetilde{P_c}$$按照传统习惯将$Z$挪到左侧，表达的就是相机坐标系中点和像素坐标系中像素的关系
$$Z\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]=K\widetilde{P_c}$$
把中间量$K$称作相机内参。$$K=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$
相机坐标$P$是由它的世界坐标$P_w$变换而来，相机位姿由$R,t$决定。那么有下式成立，
$$Z{P}_{uv}=Z\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=K(R{P}_w+t)=K(T{P}_w{)}_{(1:3)}$$
最后一个式子里面隐含着一次齐次坐标到非齐次坐标的转换($T{P}_w$的最后一维是1)，也就是$$\widetilde{P_c}=K(R{P}_w+t)=(T{P}_w{)}_{(1:3)}=\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]$$
两边除以$Z$, 所以，$$P_{uv}=\frac{1}{Z}K(T{P}_w{)}_{(1:3)}=\frac{1}{Z}K\widetilde{P_c}=K\left[\begin{array}{c}\frac{X}{Z}\\ \frac{Y}{Z}\\ 1\end{array}\right]=K{P}_c$$
其中$P_c=\left[\begin{array}{c}\frac{X}{Z}\\ \frac{Y}{Z}\\ 1\end{array}\right]$称为归一化坐标，二维的齐次坐标，它位于相机前方$z=1$的平面上，叫做归一化平面。
其实到现在才理解了什么是归一化平面，这个平面其实是相机坐标系下的一个平面，利用3d点除以z得到的平面。

变换过程总结：
世界坐标系下点$P_w\stackrel{R,t或者T}{}\widetilde{P_c}=R{P}_w+t=\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]\stackrel{投影到归一化平面}{}{P}_c=\left[\begin{array}{c}\frac{X}{Z}\\ \frac{Y}{Z}\\ 1\end{array}\right]\stackrel{经过相机内参}{}{P}_{uv}=K{P}_c$

1.2 畸变

• 径向畸变
  透镜的形状引起，有桶形失真和枕形失真。
• 切向畸变
  相机组装过程不能使透镜和成像平面严格平行引起。

一般使用的去畸变处理方法：先对整张图像去畸变，得到去畸变后的图像，然后讨论图像上点的空间位置。

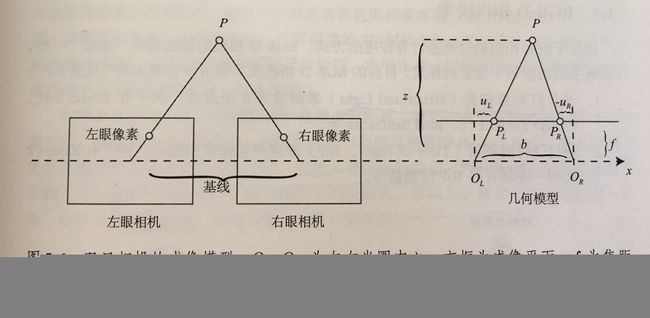
1.3 双目相机模型

根据三角形相似得到
$$\frac{z-f}{z}=\frac{b-u_L+u_R}{b}$$
整理得到
$$z=\frac{fb}{d},d=u_L-u_R$$

1.4 RGBD相机模型

原理

• 红外结构光
• 飞行时间法

2 图像的存储和访问

2.1 图像的存储

例如一张宽度为640像素，高度为480像素的灰度图(0~255)表示为

//unsigned char image[h][w];
unsigned char image[480][640];

像素坐标原点位于图像的左上角，X轴向右。Y轴向下，Z轴向前(里)。

• 数组的行 → \xrightarrow{\quad} ​图像的高度 → \xrightarrow{\quad} ​$Y$轴
• 数组的列 → \xrightarrow{\quad} ​图像的宽度$X$轴

unsigned char pixel = image[y][x]

2.2 图像的通道

• 灰度图使用一个unsigned char来表示8位数据(0~255)。
• 彩色图像需要用到通道的概念。常见的彩色图像使用三个通道来表示，每个通道由8位整数来表示，这样的话一个像素占用24位空间。
• 通道的顺序在opencv中是BGR的顺序，如果还想表达图像的透明度，可以使用RGBA四个通道。

2.3 opencv图像像素的遍历

先定位到某一行，在到某一列，再到某一个通道，最后是某一个像素。

cv::Mat image = cv::read("lena.png");
for (size_t y=0; y(y);
        unsigned char data_ptr = &row_ptr[x*image.channels()];
        
        for(int c=0; c!=image.channels();c++)
        {
            unsigned char data = data_ptr[c];
        }
    }
}