使用TensorFlow实现卷积与反卷积详细过程

卷积操作

tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None)

除去name参数用以指定该操作的name，与方法有关的一共五个参数：

• input：
  指需要做卷积的输入图像，它要求是一个Tensor，具有[batch, in_height, in_width, in_channels]这样的shape，具体含义是[训练时一个batch的图片数量, 图片高度, 图片宽度, 图像通道数]，注意这是一个4维的Tensor，要求类型为float32和float64其中之一；
• filter：
  相当于CNN中的卷积核，它要求是一个Tensor，具有[filter_height, filter_width, in_channels, out_channels]这样的shape，具体含义是[卷积核的高度，卷积核的宽度，图像通道数，卷积核个数]，要求类型与参数input相同，有一个地方需要注意，第三维in_channels，就是参数input的第四维；
• strides：
  卷积时在图像每一维的步长，这是一个一维的向量，长度4
• padding： string类型的量，只能是”SAME”,”VALID”其中之一，这个值决定了不同的卷积方式
• use_cudnn_on_gpu：
  bool类型，是否使用cudnn加速，默认为true

结果返回一个Tensor，这个输出，就是我们常说的feature map

---

实现

那么TensorFlow的卷积具体是怎样实现的呢，用一些例子去解释它：

1.考虑一种最简单的情况，现在有一张3×3单通道的图像（对应的shape：[1，3，3，1]），用一个1×1的卷积核（对应的shape：[1，1，1，1]）去做卷积，最后会得到一张3×3的feature map；

2.增加图片的通道数，使用一张3×3五通道的图像（对应的shape：[1，3，3，5]），用一个1×1的卷积核（对应的shape：[1，1，1，1]）去做卷积，仍然是一张3×3的feature map，这就相当于每一个像素点，卷积核都与该像素点的每一个通道做点积；

input = tf.Variable(tf.random_normal([1,3,3,5]))
filter = tf.Variable(tf.random_normal([1,1,5,1]))

op = tf.nn.conv2d(input, filter, strides=[1, 1, 1, 1], padding='VALID')

3.把卷积核扩大，现在用3×3的卷积核做卷积，最后的输出是一个值，相当于情况2的feature map所有像素点的值求和

input = tf.Variable(tf.random_normal([1,3,3,5]))
filter = tf.Variable(tf.random_normal([3,3,5,1]))

op = tf.nn.conv2d(input, filter, strides=[1, 1, 1, 1], padding='VALID')

4.使用更大的图片将情况2的图片扩大到5×5，仍然是3×3的卷积核，令步长为1，输出3×3的feature map

.....
.xxx.
.xxx.
.xxx.
.....

5.上面我们一直令参数padding的值为‘VALID’（不填充），当其为‘SAME’时（关于两种方式，参考链接），表示卷积核可以停留在图像边缘，如下，输出5×5的feature map

input = tf.Variable(tf.random_normal([1,5,5,5]))
filter = tf.Variable(tf.random_normal([3,3,5,1]))

op = tf.nn.conv2d(input, filter, strides=[1, 1, 1, 1], padding='SAME')

6.如果卷积核有多个

input = tf.Variable(tf.random_normal([1,5,5,5]))
filter = tf.Variable(tf.random_normal([3,3,5,7]))

op = tf.nn.conv2d(input, filter, strides=[1, 1, 1, 1], padding='SAME')

此时输出7张5×5的feature map

7.步长不为1的情况，文档里说了对于图片，因为只有两维，通常strides取[1，stride，stride，1]

input = tf.Variable(tf.random_normal([1,5,5,5]))
filter = tf.Variable(tf.random_normal([3,3,5,7]))

op = tf.nn.conv2d(input, filter, strides=[1, 2, 2, 1], padding='SAME')

8.如果batch值不为1，同时输入10张图

input = tf.Variable(tf.random_normal([10,5,5,5]))
filter = tf.Variable(tf.random_normal([3,3,5,7]))

op = tf.nn.conv2d(input, filter, strides=[1, 2, 2, 1], padding='SAME')

每张图，都有7张3×3的feature map，输出的shape就是[10，3，3，7]

---

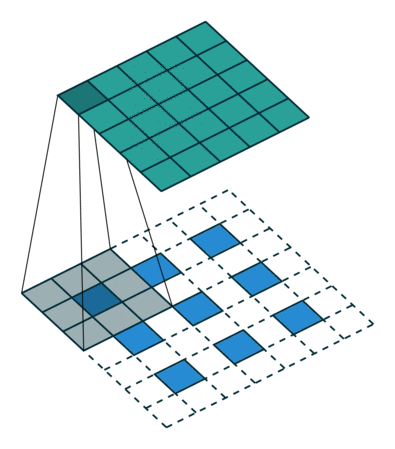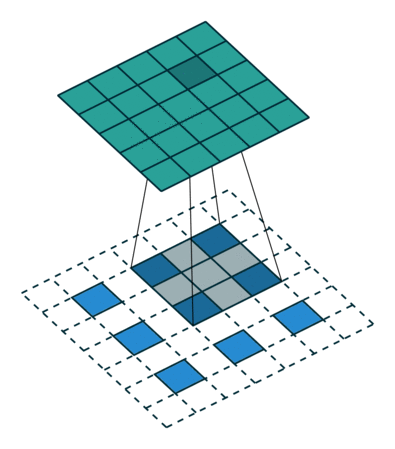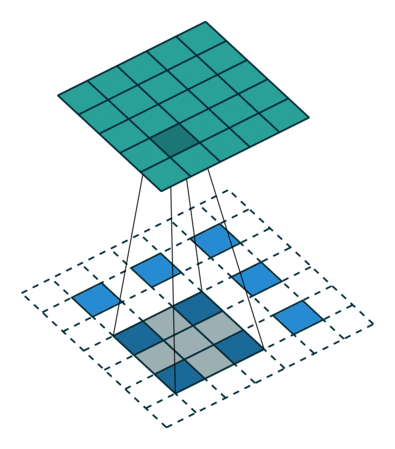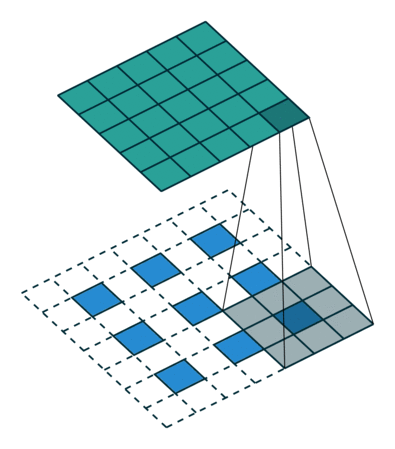
反卷积

conv2d_transpose(value, filter, output_shape, strides, padding="SAME", 
data_format="NHWC", name=None)

除去name参数用以指定该操作的name，与方法有关的一共六个参数：

• 第一个参数value：
  指需要做反卷积的输入图像，它要求是一个Tensor
• 第二个参数filter：
  卷积核，它要求是一个Tensor，具有[filter_height, filter_width, out_channels, in_channels]这样的shape，具体含义是[卷积核的高度，卷积核的宽度，卷积核个数，图像通道数]
• 第三个参数output_shape：
  反卷积操作输出的shape，细心的同学会发现卷积操作是没有这个参数的，那这个参数在这里有什么用呢？下面会解释这个问题
• 第四个参数strides：
  反卷积时在图像每一维的步长，这是一个一维的向量，长度4
• 第五个参数padding：
  string类型的量，只能是”SAME”,”VALID”其中之一，这个值决定了不同的卷积方式
• 第六个参数data_format：
  string类型的量，’NHWC’和’NCHW’其中之一，这是tensorflow新版本中新加的参数，它说明了value参数的数据格式。‘NHWC’指tensorflow标准的数据格式[batch, height, width, in_channels]，‘NCHW’指Theano的数据格式,[batch, in_channels，height, width]，当然默认值是’NHWC’

首先定义一个单通道图和3个卷积核

x1 = tf.constant(1.0, shape=[1,3,3,1])  
kernel = tf.constant(1.0, shape=[3,3,3,1])  

再定义一些图

x2 = tf.constant(1.0, shape=[1,6,6,3])  
x3 = tf.constant(1.0, shape=[1,5,5,3])  

x2是6×6的3通道图，x3是5×5的3通道图
好了，接下来对x3做一次卷积操作

y2 = tf.nn.conv2d(x3, kernel, strides=[1,2,2,1], padding="SAME")  

所以返回的y2是一个单通道的图，如果你了解卷积过程，很容易看出来y2是[1，3，3，1]的Tensor，y2的结果如下：

[[[[ 12.]
   [ 18.]
   [ 12.]]

  [[ 18.]
   [ 27.]
   [ 18.]]

  [[ 12.]
   [ 18.]
   [ 12.]]]]

又一个很重要的部分！tf.nn.conv2d中的filter参数，是[filter_height, filter_width, in_channels, out_channels]的形式，而tf.nn.conv2d_transpose中的filter参数，是[filter_height, filter_width, out_channels，in_channels]的形式，注意in_channels和out_channels反过来了！因为两者互为反向，所以输入输出要调换位置。反卷积核是原卷积核的转置矩阵，所以反卷积又称为转置卷积

既然y2是卷积操作的返回值，那我们当然可以对它做反卷积，反卷积操作返回的Tensor，应该和x3的shape是一样的（不难理解，因为是卷积的反过程）

y3 = tf.nn.conv2d_transpose(y2,kernel,output_shape=[1,5,5,3], 
strides=[1,2,2,1],padding="SAME")  

好，现在返回的y3果然是[1，5，5，3]的Tensor，结果如下：

[[[[ 12.  12.  12.]  
   [ 30.  30.  30.]  
   [ 18.  18.  18.]  
   [ 30.  30.  30.]  
   [ 12.  12.  12.]]  

  [[ 30.  30.  30.]  
   [ 75.  75.  75.]  
   [ 45.  45.  45.]  
   [ 75.  75.  75.]  
   [ 30.  30.  30.]]  

  [[ 18.  18.  18.]  
   [ 45.  45.  45.]  
   [ 27.  27.  27.]  
   [ 45.  45.  45.]  
   [ 18.  18.  18.]]  

  [[ 30.  30.  30.]  
   [ 75.  75.  75.]  
   [ 45.  45.  45.]  
   [ 75.  75.  75.]  
   [ 30.  30.  30.]]  

  [[ 12.  12.  12.]  
   [ 30.  30.  30.]  
   [ 18.  18.  18.]  
   [ 30.  30.  30.]  
   [ 12.  12.  12.]]]]  

这个结果是怎么得来的？可以用一张动图来说明

又如

看起来，tf.nn.conv2d_transpose的output_shape似乎是多余的，因为知道了原图，卷积核，步长显然是可以推出输出图像大小的，那为什么要指定output_shape呢？
看这样一种情况：

y4 = tf.nn.conv2d(x2, kernel, strides=[1,2,2,1], padding="SAME")  

我们把上面的x2也做卷积，获得shape为[1，3，3，1]的y4如下：

[[[[ 27.]  
   [ 27.]  
   [ 18.]]  

  [[ 27.]  
   [ 27.]  
   [ 18.]]  

  [[ 18.]  
   [ 18.]  
   [ 12.]]]]  

[1，6，6，3]和[1，5，5，3]的图经过卷积得到了相同的大小，[1，3，3，1]
让我们再反过来看，那么[1，3，3，1]的图反卷积后得到什么呢？产生了两种情况。所以这里指定output_shape是有意义的，当然随意指定output_shape是不允许的，如下情况程序会报错：

y5 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,10,10,3],
strides=[1,2,2,1],padding="SAME")  

程序清单：

import tensorflow as tf  

x1 = tf.constant(1.0, shape=[1,3,3,1])  

x2 = tf.constant(1.0, shape=[1,6,6,3])  

x3 = tf.constant(1.0, shape=[1,5,5,3])  

kernel = tf.constant(1.0, shape=[3,3,3,1])  



y1 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,6,6,3],  
    strides=[1,2,2,1],padding="SAME")  

y2 = tf.nn.conv2d(x3, kernel, strides=[1,2,2,1], padding="SAME")  

y3 = tf.nn.conv2d_transpose(y2,kernel,output_shape=[1,5,5,3],  
    strides=[1,2,2,1],padding="SAME")  

y4 = tf.nn.conv2d(x2, kernel, strides=[1,2,2,1], padding="SAME")  

''''' 
Wrong!!This is impossible 
y5 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,10,10,3],
strides=[1,2,2,1],padding="SAME") 
'''  
sess = tf.Session()  
tf.global_variables_initializer().run(session=sess)  
x1_decov, x3_cov, y2_decov, x2_cov=sess.run([y1,y2,y3,y4])  
print(x1_decov.shape)  
print(x3_cov.shape)  
print(y2_decov.shape)  
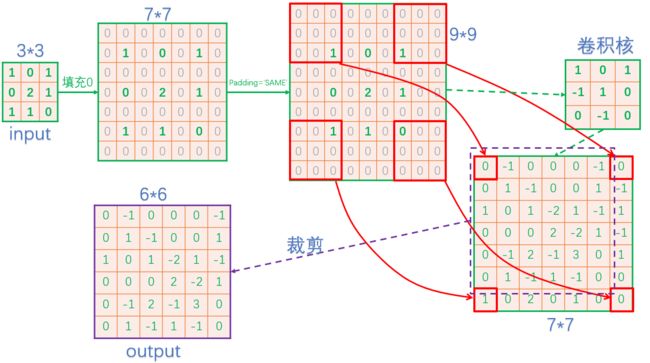
print(x2_cov.shape)  

---

python实现卷积操作

import numpy as np
input_data=[
              [[1,0,1,2,1],
               [0,2,1,0,1],
               [1,1,0,2,0],
               [2,2,1,1,0],
               [2,0,1,2,0]],

               [[2,0,2,1,1],
                [0,1,0,0,2],
                [1,0,0,2,1],
                [1,1,2,1,0],
                [1,0,1,1,1]] 
            ]
weights_data=[ 
               [[ 1, 0, 1],
                [-1, 1, 0],
                [ 0,-1, 0]],
               [[-1, 0, 1],
                [ 0, 0, 1],
                [ 1, 1, 1]] 

           ]

#fm:[h,w]
#kernel:[k,k]
#return rs:[h,w] 
def compute_conv(fm,kernel):
    [h,w]=fm.shape
    [k,_]=kernel.shape 
    r=int(k/2)
    #定义边界填充0后的map
    padding_fm=np.zeros([h+2,w+2],np.float32)
    #保存计算结果
    rs=np.zeros([h,w],np.float32)
    #将输入在指定该区域赋值，即除了4个边界后，剩下的区域
    padding_fm[1:h+1,1:w+1]=fm 
    #对每个点为中心的区域遍历
    for i in range(1,h+1):
        for j in range(1,w+1): 
            #取出当前点为中心的k*k区域
            roi=padding_fm[i-r:i+r+1,j-r:j+r+1]
            #计算当前点的卷积,对k*k个点点乘后求和
            rs[i-1][j-1]=np.sum(roi*kernel)

    return rs

def my_conv2d(input,weights):
    [c,h,w]=input.shape
    [_,k,_]=weights.shape
    outputs=np.zeros([h,w],np.float32)

    #对每个feature map遍历，从而对每个feature map进行卷积
    for i in range(c):
        #feature map==>[h,w]
        f_map=input[i]
        #kernel ==>[k,k]
        w=weights[i]
        rs =compute_conv(f_map,w)
        outputs=outputs+rs   

    return outputs

def main():  

    #shape=[c,h,w]
    input = np.asarray(input_data,np.float32)
    #shape=[in_c,k,k]
    weights =  np.asarray(weights_data,np.float32) 
    rs=my_conv2d(input,weights) 
    print(rs) 


if __name__=='__main__':
    main()