深度学习小项目——图像风格迁移(基于Tensorflow)
基于神经网络的风格迁移算法 “A Neural Algorithm of Artistic Style” 最早由 Gatys 等人在 2015 年提出,随后发表在 CVPR 2016 上。斯坦福大学的 Justin Johnson(cs231n 课程的主讲人之一)给出了 Torch 实现 neural-style。除此之外,这篇文章的作者另外还建立了一个在线艺术风格迁移的网站,deepart.io。在介绍主要内容之前,先直观看下什么是艺术风格迁移,如图 1 所示,给定内容图像(第一行左边图像)以及风格图像(左下角图像)可以生成特定风格下的混合图像。网络多次运算后,人眼很难判断出该图像是否为梵高或者毕加索的真迹。
图像内容和图像风格定义
艺术风格迁移的核心思想就是,可以从一副图像中提取出“风格 style”(比如梵高的夜空风格)以及“内容 content”(比如你能在画中看出河边有匹马)。你可以告诉机器,把 A 用 B 的风格再画一遍。但是怎么用数学语言具体定义风格和内容呢?在这里通过引入一个 VGG19 深度网络来具体阐述相关的含义。
VGG19深度网络
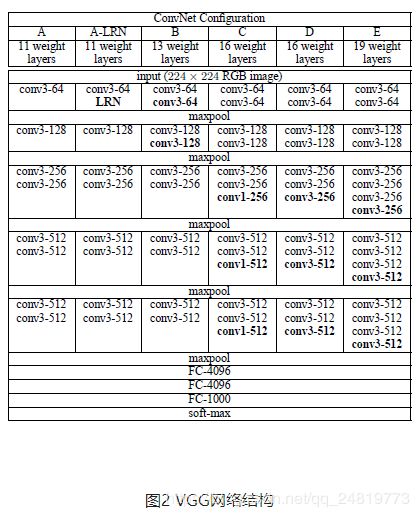
VGG 是 ImageNet2014 年的图像识别大赛识别定位组的冠军,几种不同深度的 VGG 网络结构如图 2 所示:
每一层神经网络都会利用上一层的输出来进一步提取更加复杂的特征,直到复杂到能被用来识别物体为止,所以每一层都可以被看做很多个局部特征的提取器。VGG19 在物体识别方面的精度甩了之前的算法一大截,之后的物体识别系统也基本都改用深度学习了。
因为 VGG19 的优秀表现,引起了很多兴趣和讨论,但是 VGG19 具体内部在做什么其实很难理解,因为每一个神经元内部参数只是一堆数字而已。每个神经元有几百个输入和几百个输出,一个一个去梳理清楚神经元和神经元之间的关系太难。于是有人想出来一种办法:虽然我们不知道神经元是怎么工作的,但是如果我们知道了它的激活条件,会不会能对理解神经网络更有帮助呢?于是他们编了一个程序,(用的方法叫 back propagation,和训练神经网络的方法一样,只是倒过来生成图片。)把每个神经元所对应的能激活它的图片找了出来,之前的那幅特征提取示意图就是这么生成的。
代码:
# -*- coding: utf-8 -*-
# @Time : 2019/2/21 18:03
# @Author : Chaucer_Gxm
# @Email : [email protected]
# @File : Code_Tensorflow.py
# @GitHub : https://github.com/Chaucergit/Code-and-Algorithm
# @blog : https://blog.csdn.net/qq_24819773
# @Software: PyCharm
import tensorflow as tf
import numpy as np
import scipy.io
import scipy.misc
import os
import time
def the_current_time():
print(time.strftime('%Y-%m-%d %H:%M:%S', time.localtime(int(time.time()))))
CONTENT_IMG = 'flower.jpg'
STYLE_IMG = 'style5.jpg'
OUTPUT_DIR = 'Tensorflow_Picture2/'
# 如果没有相应的文件夹就自动创建文件夹
if not os.path.exists(OUTPUT_DIR):
os.mkdir(OUTPUT_DIR)
IMAGE_W = 270
IMAGE_H = 480
COLOR_C = 3
NOSIE_RATIO = 0.7
BETE = 5
ALPHA = 100
VGG_MODEL = 'imagenet-vgg-verydeep-19.mat'
MEAN_VALUES = np.array([123.68, 116.779, 103.939]).reshape((1, 1, 1, 3))
def load_vgg_model(path):
vgg = scipy.io.loadmat(path)
vgg_layers = vgg['layers']
def _weights(layer, expected_layer_name):
W = vgg_layers[0][layer][0][0][2][0][0]
b = vgg_layers[0][layer][0][0][2][0][1]
layer_name = vgg_layers[0][layer][0][0][0][0]
assert layer_name == expected_layer_name
return W, b
def _conv2d_relu(prev_layer, layer, layer_name):
W, b = _weights(layer, layer_name)
W = tf.constant(W)
b = tf.constant(np.reshape(b, (b.size)))
return tf.nn.relu(tf.nn.conv2d(prev_layer, filter=W, strides=[1, 1, 1, 1], padding='SAME') + b)
def _avgpool(prev_layer):
return tf.nn.avg_pool(prev_layer, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
graph = {}
graph['input'] = tf.Variable(np.zeros((1, IMAGE_H, IMAGE_W, COLOR_C)), dtype='float32')
graph['conv1_1'] = _conv2d_relu(graph['input'], 0, 'conv1_1')
graph['conv1_2'] = _conv2d_relu(graph['conv1_1'], 2, 'conv1_2')
graph['avgpool1'] = _avgpool(graph['conv1_2'])
graph['conv2_1'] = _conv2d_relu(graph['avgpool1'], 5, 'conv2_1')
graph['conv2_2'] = _conv2d_relu(graph['conv2_1'], 7, 'conv2_2')
graph['avgpool2'] = _avgpool(graph['conv2_2'])
graph['conv3_1'] = _conv2d_relu(graph['avgpool2'], 10, 'conv3_1')
graph['conv3_2'] = _conv2d_relu(graph['conv3_1'], 12, 'conv3_2')
graph['conv3_3'] = _conv2d_relu(graph['conv3_2'], 14, 'conv3_3')
graph['conv3_4'] = _conv2d_relu(graph['conv3_3'], 16, 'conv3_4')
graph['avgpool3'] = _avgpool(graph['conv3_4'])
graph['conv4_1'] = _conv2d_relu(graph['avgpool3'], 19, 'conv4_1')
graph['conv4_2'] = _conv2d_relu(graph['conv4_1'], 21, 'conv4_2')
graph['conv4_3'] = _conv2d_relu(graph['conv4_2'], 23, 'conv4_3')
graph['conv4_4'] = _conv2d_relu(graph['conv4_3'], 25, 'conv4_4')
graph['avgpool4'] = _avgpool(graph['conv4_4'])
graph['conv5_1'] = _conv2d_relu(graph['avgpool4'], 28, 'conv5_1')
graph['conv5_2'] = _conv2d_relu(graph['conv5_1'], 30, 'conv5_2')
graph['conv5_3'] = _conv2d_relu(graph['conv5_2'], 32, 'conv5_3')
graph['conv5_4'] = _conv2d_relu(graph['conv5_3'], 34, 'conv5_4')
graph['avgpool5'] = _avgpool(graph['conv5_4'])
return graph
def content_loss_func(sess, model):
def _content_loss(p, x):
N = p.shape[3]
M = p.shape[1] * p.shape[2]
return (1/(4 * N * M)) * tf.reduce_sum(tf.pow(x-p, 2))
return _content_loss(sess.run(model['conv4_2']), model['conv4_2'])
STYLE_LAYERS = [('conv1_1', 0.5), ('conv2_1', 1.0), ('conv3_1', 1.5), ('conv4_1', 3.0), ('conv5_1', 4.0)]
def style_loss_func(sess, model):
def _gram_matrix(F, N, M):
Ft = tf.reshape(F, (M, N))
return tf.matmul(tf.transpose(Ft), Ft)
def _style_loss(a, x):
N = a.shape[3]
M = a.shape[1] * a.shape[2]
A = _gram_matrix(a, N, M)
G = _gram_matrix(x, N, M)
return (1 / (4 * N ** 2 * M ** 2)) * tf.reduce_sum(tf.pow(G - A, 2))
return sum([_style_loss(sess.run(model[layer_name]), model[layer_name]) * w for layer_name, w in STYLE_LAYERS])
def generate_noise_image(content_image, noise_ratio=NOSIE_RATIO):
noise_image = np.random.uniform(-20, 20, (1, IMAGE_H, IMAGE_W, COLOR_C)).astype('float32')
input_image = noise_image * noise_ratio + content_image * (1 - noise_ratio)
return input_image
def load_image(path):
image = scipy.misc.imread(path)
image = scipy.misc.imresize(image, (IMAGE_H, IMAGE_W))
image = np.reshape(image, ((1, ) + image.shape))
image = image - MEAN_VALUES
return image
def save_image(path, image):
image = image + MEAN_VALUES
image = image[0]
image = np.clip(image, 0, 255).astype('uint8')
scipy.misc.imsave(path, image)
the_current_time()
with tf.Session() as sess:
content_image = load_image(CONTENT_IMG)
style_image = load_image(STYLE_IMG)
model = load_vgg_model(VGG_MODEL)
input_image = generate_noise_image(content_image)
sess.run(tf.global_variables_initializer())
sess.run(model['input'].assign(content_image))
content_loss = content_loss_func(sess, model)
sess.run(model['input'].assign(style_image))
style_loss = style_loss_func(sess, model)
total_loss = BETE * content_loss + ALPHA * style_loss
optimizer = tf.train.AdamOptimizer(2.0)
train = optimizer.minimize(total_loss)
sess.run(tf.global_variables_initializer())
sess.run(model['input'].assign(input_image))
ITERATIONS = 2000
for i in range(ITERATIONS):
sess.run(train)
if i % 100 == 0:
output_image = sess.run(model['input'])
the_current_time()
print('Iteration %d' % i)
print('Cost: ', sess.run(total_loss))
save_image(os.path.join(OUTPUT_DIR, 'output_%d.jpg' % i), output_image)
执行前效果:
执行后的效果:
基于神经网络的图像风格迁移论文链接:
**Texture synthesis using convolutional neural networks
***A neural algorithm of artistic style
*Combining Markov Random Fields and Convolutional Neural Networks for Image Synthesis
*Texture networks: Feed-forward synthesis of textures and stylized images
A Learned Representation For Artistic Style
Fast Patch-based Style Transfer of Arbitrary Style
*Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization
Visual Attribute Transfer through Deep Image Analogy
参考博文的链接:https://www.imooc.com/article/details/id/32660