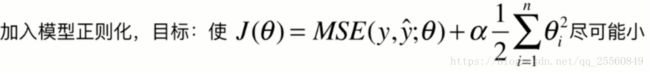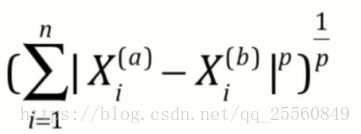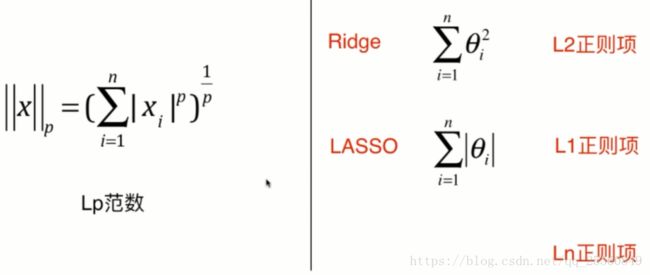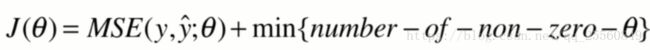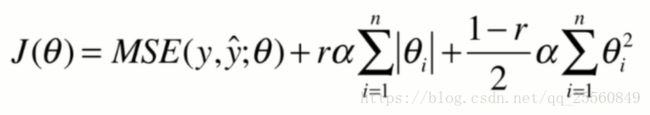机器学习基础-6.多项式回归

一、多项式回归

1.思想

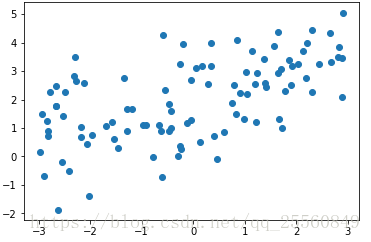
线性回归的局限性是只能应用于存在线性关系的数据中，但是在实际生活中，很多数据之间是非线性关系，虽然也可以用线性回归拟合非线性回归，但是效果将会很差，这时候就需要对线性回归模型进行改进，使之能够拟合非线性数据。

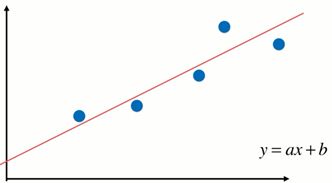
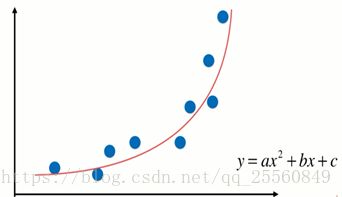
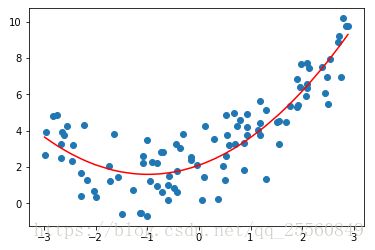
如图所示，左图为数据呈现出线性关系，用线性回归可以得到较好的拟合效果。右图数据呈现非线性关系，需要多多项式回归模型。多项式回归是在线性回归基础上进行改进，相当于为样本再添加特征项。如右图所示，为样本添加一个x^2的特征项，可以较好地拟合非线性的数据。

2.代码实现

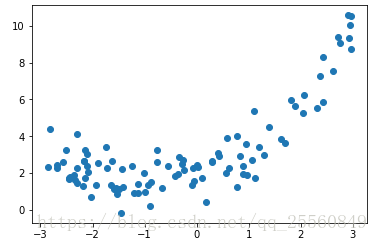
准备数据，并引入随机噪声。

import numpy as np
import matplotlib.pyplot as plt

x = np.random.uniform(-3,3, size=100)
X = x.reshape(-1,1) #接下来的代码要区分好X和x
y = 0.5 * x**2 +x +2 + np.random.normal(0,1,size=100)
plt.scatter(x,y)
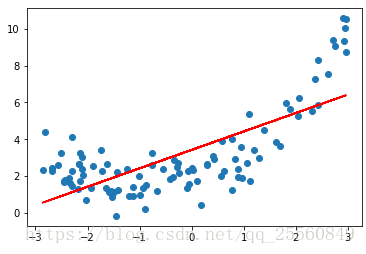
plt.show()

首先采用线性回归的方式。

#首先用线性回归的方式，可以看出拟合效果很差
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)
y_predict = lin_reg.predict(X)
plt.scatter(x,y)
plt.plot(x,y_predict,color='r')
plt.show()

现在采用多项式回归。

x2 = np.hstack([X,X**2]) #这里给样本X再引入1个特征项，现在的特征就有2个
lin_reg2 = LinearRegression()
lin_reg2.fit(x2,y)
y_predict2 = lin_reg2.predict(x2)
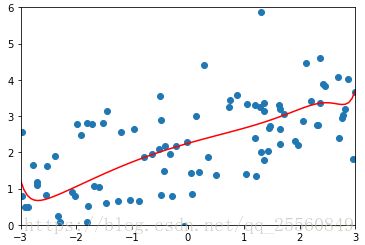
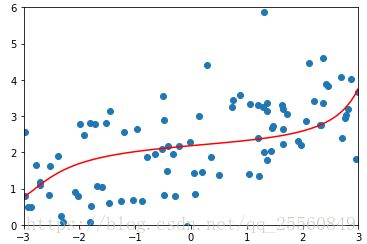
plt.scatter(x,y)
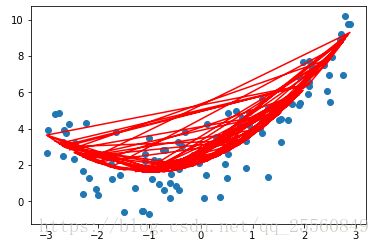
plt.plot(np.sort(x),y_predict2[np.argsort(x)],color='r') #绘制的时候要注意，因为x是无序的，为了画出如下图平滑的线条，需要先将x进行排序，y_predict2按照x从的大小的顺序进行取值，否则绘制出的如右下图。

lin_reg2.coef_ ,in_reg2.intercept_#检查拟合的系数，和原来预设的系数很接近

3.sklearn

sklearn中也封装了为样本添加特征项的工具，在数据预处理模块中。

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2) #设置最多添加几次幂的特征项
poly.fit(X)
x2 = poly.transform(X)
#x2.shape 这个时候x2有三个特征项，因为在第1列加入1列1，并加入了x^2项
from sklearn.linear_model import LinearRegression #接下来的代码和线性回归一致
lin_reg2 = LinearRegression()
lin_reg2.fit(x2,y)
y_predict2 = lin_reg2.predict(x2)
plt.scatter(x,y)
# plt.plot(np.sort(x),y_predict2[np.argsort(x)],color='r')
plt.plot(x,y_predict2,color='r')
lin_reg2.coef_,lin_reg2.intercept_ #绘制的图像和预测所得的值和上面完全一致，唯一不同的是lin_reg2.coef_有3个系数，第一个系数值为0

当PolynomialFeatures(degree=3)时，对于原本有2个特征的样本将会产生共10个项的样本，具体的生成方式通过下图便可得出规律，这里不再总结。

4.pipeline

pipeline可以将相同的处理过程进行封装，简化代码。

import numpy as np  
import matplotlib.pyplot as plt 
x = np.random.uniform(-3,3, size=100)
X = x.reshape(-1,1)
y = 0.5 * x**2 +x +2 + np.random.normal(0,1,size=100)

from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

poly_reg = Pipeline(degree)([ #这里将三个处理步骤进行了封装，将数据传入poly_reg之后，将会智能地沿着该管道进行处理
    ("poly",PolynomialFeatures(degree=degree))，
    ("std_scaler",StandardScaler())，
    ("lin_reg",LinearRegression())    
])

poly_reg.fit(X,y) 
y_predict = poly_reg.predict(X)
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='r') #效果和之前代码一致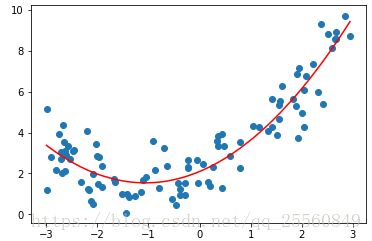

二、过拟合和欠拟合

过拟合指的是数据进行过度训练，得出来的训练模型虽然对于训练数据来说，拟合地非常好，但是对于测试数据，将会有糟糕的表现，原因是过度地拟合将会把噪声也极大地引入。

import numpy as np  
import matplotlib.pyplot as plt 

np.random.seed(666) #为了反复测试，这里将随机种子固定
x = np.random.uniform(-3.,3., size=100)
X = x.reshape(-1,1)
y = 0.5 * x**2 +x +2 + np.random.normal(0,1,size=100)
from sklearn.metrics import mean_squared_error #引入均方误差用来测试拟合的分数
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

def PolynomialRegression(degree):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),
        ("std_scaler",StandardScaler()),
        ("lin_reg",LinearRegression())    
    ])

现在不断改变degree值，观察拟合结果。

poly_reg = PolynomialRegression(degree=10)
poly_reg.fit(X,y)
y_predict = poly_reg.predict(X)
plt.scatter(x,y)
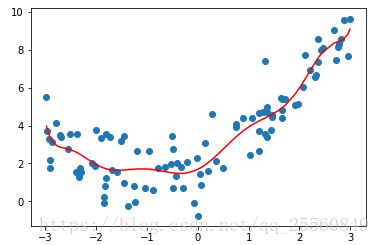
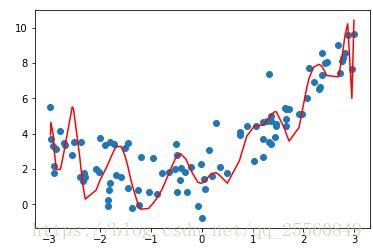
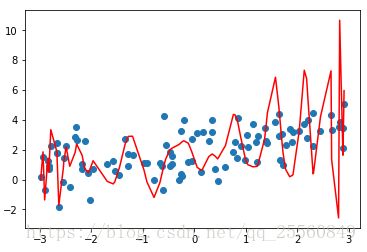
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='r')

degree=30，可以发现虽然拟合该数据较好，但是其实不符合实际的数据走势。

mean_squared_error(y,y_predict) #随着degree的增大，均方误差逐渐减小，但是实际上过拟合地越严重，效果越差

欠拟合即数据训练的不够，拟合地太过简单了，不能完整表达数据关系，如下图。

三、模型泛化能力

在过拟合和欠拟合中，训练出来的模型对于新的数据样本，预测值和真实值都会有很大的偏差，这时候模型的泛化能力较差，即预测能力较差；如果数据被正确地训练，最终能够较好地为新的数据样本做预测，则可以说该模型的泛化能力较好。目标是训练出泛化能力好的模型，而非拟合训练数据好的模型。

一般将数据集分成训练数据集和测试数据集，在训练数据集上训练的出的模型对训练数据集也有很好的结果，这个时候就可以说模型的泛化能力较强。接下来，采用均方差来衡量模型的泛化能力。均方差越小，泛化能力越强。

1.线性回归

from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(X,y,random_state=666)
lin_reg = LinearRegression()
lin_reg.fit(x_train,y_train)
y_predict = lin_reg.predict(x_test)
mean_squared_error(y_predict,y_test)

最终得到的结果为：2.2199965269396573。

2.多项式回归

poly_reg = PolynomialRegression(degree=2)
poly_reg.fit(x_train,y_train)
y_predict = poly_reg.predict(x_test)
mean_squared_error(y_predict,y_test)

最终得到的结果为：0.8035641056297901。当degree=30，结果为16.91453591949335，泛化能力明显降低。

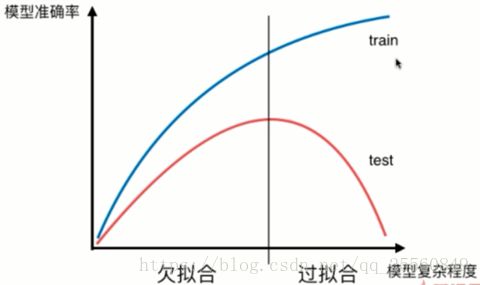
模型的准确率和模型的复杂程度一般有如下的关系，我们的目标即寻找到泛化能力最好的地方。

3.学习曲线

学习曲线能够表示出：随着训练样本的逐渐增多，算法训练出的模型的表现能力。

from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error\

x_train,x_test,y_train,y_test = train_test_split(X,y,random_state=10)

train_score = [] #用来记录训练数据拟合的程度
test_score = [] #用来记录测试数据拟合的程度
for i in range(1,76):
    lin_reg = LinearRegression()
    lin_reg.fit(x_train[:i],y_train[:i])
    y_train_predict = lin_reg.predict(x_train[:i])
    y_test_predict = lin_reg.predict(x_test)
    train_score.append(mean_squared_error(y_train_predict,y_train[:i]))
    test_score.append(mean_squared_error(y_test_predict,y_test))
plt.plot([i for i in range(1,76)],np.sqrt(test_score),label='train')
plt.plot([i for i in range(1,76)],np.sqrt(train_score),label='test')
plt.legend()
plt.show()

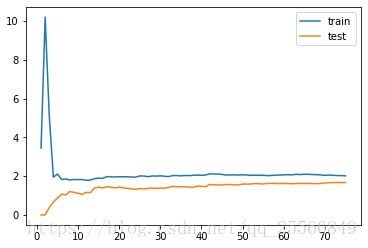
从学习曲线可以发现，随着训练样本的不断增加，训练数据的均方根误差先上升后下降，测试数据的均方根误差不断上升，二者最后都区域一个稳定值。

对上面代码进行封装。

def plot_learning_curve(algo,x_train,x_test,y_train,y_test): #algo代表不同算法
    train_score = []
    test_score = []
    for i in range(1,len(x_train)+1):
        algo.fit(x_train[:i],y_train[:i])
        y_train_predict = algo.predict(x_train[:i])
        y_test_predict = algo.predict(x_test)
        train_score.append(mean_squared_error(y_train_predict,y_train[:i]))
        test_score.append(mean_squared_error(y_test_predict,y_test))
    plt.plot([i for i in range(1,76)],np.sqrt(test_score),label='train')
    plt.plot([i for i in range(1,76)],np.sqrt(train_score),label='test')
    plt.legend()
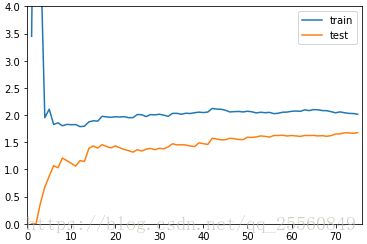
    plt.axis([0,len(x_train)+1,0,4])#限定坐标显示的范围，因为主要还是比较t_train和t_test相近的地方。
    plt.show()

对于线性回归算法。

plot_learning_curve(LinearRegression(),x_train,x_test,y_train,y_test)

对于多项式回归算法。

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
def PolynomialRegression(degree):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),
        ("std_scaler",StandardScaler()),
        ("lin_reg",LinearRegression())    
    ])
poly2_reg = PolynomialRegression(degree=2)
plot_learning_curve(poly2_reg,x_train,x_test,y_train,y_test) #可以看到稳定的值比线性回归低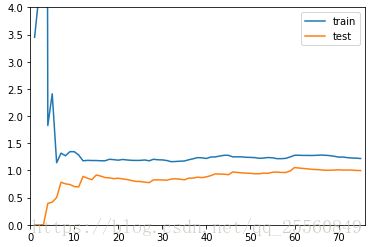

四、交叉验证

1.进行交叉验证的原因

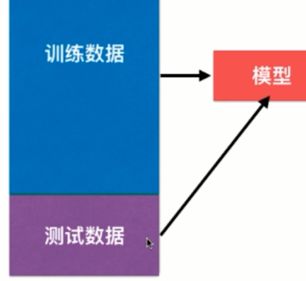
如图所示。为了得到泛化能力强的模型，将数据分为测试数据和训练数据，当模型在测试数据也有较好的拟合效果时，则可以说模型的泛化能力较强。但是依然存在一个问题，一旦训练数据得出的模型在测试数据没有得到较好的效果，则需要调整测试数据的参数，换言之，其实就是为了使模型更好地拟合测试数据集，带来的问题就是该模型对于测试数据集将可能是个过拟合的。为此将数据集分成三部分，引入验证数据集。训练数据用来训练，验证数据用来验证模型好坏并进行超参数调整，用测试数据做为最终的评判标准。

     

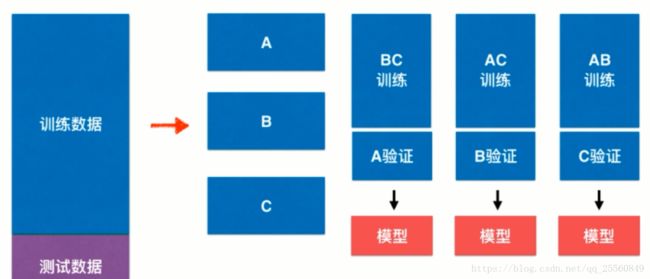
但是这里同样存在可能过拟合验证数据的问题，因此需要进行随机处理，所以就引入了交叉验证。如下图所示，将训练数据切分成多份（3份为例），对切分的数据进行组合，整合成训练数据和验证数据，每个整合训练出不同的模型，将这3个模型的性能指标取平均值，作为衡量当前算法得到模型的性能指标。

2.代码实现

首先用split方式。

#首先使用传统的split方式
import numpy as np 
from sklearn import datasets
digits = datasets.load_digits()
x = digits.data
y = digits.target
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.4,random_state=10)
from sklearn.neighbors import KNeighborsClassifier
bestscore,bestp,bestk=0,0,0
for k in range(2,11):
    for p in range(1,6):
        knn = KNeighborsClassifier(weights='distance',n_neighbors=k,p=p)
        knn.fit(x_train,y_train)
        score = knn.score(x_test,y_test)
        if bestscore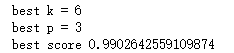

使用交叉验证方式。

from sklearn.model_selection import cross_val_score #导入函数
bestscore,bestp,bestk=0,0,0
for k in range(2,11):
    for p in range(1,6):
        knn = KNeighborsClassifier(weights='distance',n_neighbors=k,p=p)
        scores = cross_val_score(knn,x_train,y_train) #这里使用交叉验证，scores有三个值，需要求平均，可以再传入cv参数，默认为3份
        score = np.mean(scores)
        if bestscore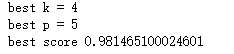

可以发现，这个和上面split求得的最佳值不太一样，上面用简单的split方式得到的可能仅仅是过拟合的模型。得到最佳参数后，现在就需要应用x_test数据进行验证。

bestknn = KNeighborsClassifier(weights="distance",n_neighbors=4,p=5)
bestknn.fit(x_train,y_train)
bestknn.score(x_test,y_test)

因此可以说，通过三交叉验证的方式，最终获得模型的准确率为98，可信度较高。

这里回顾下网格搜索。这里的CV即cross validation，交叉验证。

from sklearn.model_selection import GridSearchCV
param_grid = [  
    {  
         'weights': ['uniform'],  
       'n_neighbors':[i for i in range(1,11)]  
   },  
    {  
         'weights': ['distance'],  
       'n_neighbors': [i for i in range(1,11)],  
       'p': [i for i in range(1,6)]  
    }  
] 

交叉验证可以发展为留一法（loo-cv，leave-one-out cross validation）。即有m个样本，将m-1个样本作为训练数据，只留一个作为最终预测。这时候将会完全不受随机的影响，最接近模型真正的性能指标，但是缺点显而易见，计算量将会十分巨大。

五、偏差、方差权衡

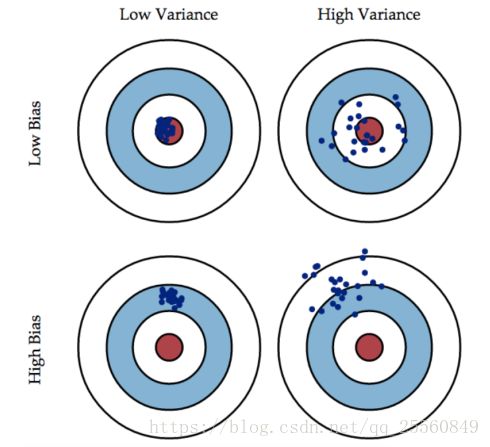
偏差描述样本偏离实际值的情况，方差描述样本的分布疏密情况。下图中红色点为真值，蓝色点为样本点，描绘了不同偏差和方差分布情况。

模型的误差=方差+偏差+不可避免的误差（例如测量带来的精度损失、噪声等）

导致偏差的原因，可能是对模型的假设是错误的，例如用线性的假设去预测非线性数据，或者采用的特征和预测其实没有关系。在机器学习中，一般不会出现采取的特征和预测毫无相关的情况，事实上导致高偏差的原因主要是欠拟合。

导致方差的原因，通常是因为模型太过复杂，一点的数据抖动都将会影响到结果，过拟合是导致高方差的主要原因。

非参数学习通常都是高方差，因为不对数据进行任何的假设。例如KNN、决策树，高度依赖样本数据。

参数学习通常都是高偏差算法，因为对数据具有极强的假设，例如线性回归。

偏差和方差通常是相互矛盾的，降低偏差将会提高方差，降低方差将会提高偏差。在算法领域，主要的挑战来自方差。

解决的方法：降低模型复杂度、减少数据维度，降噪；增加样本数；使用验证集、模型正则化等。

六、模型正则化

1.岭回归正则化

图下图所示，当degree很大时，模型易出现过拟合，具体表现就是某些系数值θ，将会非常大，因此需要对模型正则化：限制参数的大小。

注意：模型正则化时，θ从1开始，而不是0开始，原因是θ0仅仅影响曲线的整体高度，不进行限制。α是个超参数，可以进行调整。这种限制θ参数大小的方式通常被称为岭回归（ridge regression）。

2.岭回归代码实现

import numpy as np  
import matplotlib.pyplot as plt 
x = np.random.uniform(-3.,3., size=100)
X = x.reshape(-1,1)
y = 0.5 * x + +2 + np.random.normal(0,1,size=100)
plt.scatter(x,y)
plt.show()

import numpy as np  
import matplotlib.pyplot as plt 

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

np.random.seed(666)
x_train,x_test,y_train,y_test = train_test_split(X,y,random_state=10)

def PolynomialRegression(degree):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),
        ("std_scaler",StandardScaler()),
        ("lin_reg",LinearRegression())    
    ])
def plot_model(model): #绘制图像的代码封装，为了方便使用，直接传入模型即可
    x_plot = np.linspace(-3,3,100).reshape(100,1)
    y_plot = model.predict(x_plot)
    plt.scatter(x,y)
    plt.plot(x_plot[:,0],y_plot,color='r')
    plt.axis([-3,3,0,6])
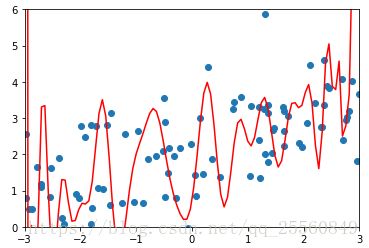
    plt.show()

首先使用多项式回归，可以看到出现了过拟合。

poly_reg = PolynomialRegression(degree=50)
poly_reg.fit(X,y)
plot_model(poly_reg)

接着使用加入岭回归正则化的多项式回归。

from sklearn.linear_model import Ridge
def RridgeRegression(degree,alpha): #修改管道
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),
        ("std_scaler",StandardScaler()),
        ("lin_reg",Ridge(alpha=alpha))    #加入岭回归
    ])
ridge1 = RridgeRegression(20,0.0001)
ridge1.fit(x_train,y_train)
y_test = ridge1.predict(x_test)
#mean_squared_error(y_test,x_test)
plot_model(ridge1)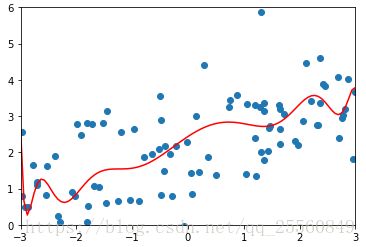

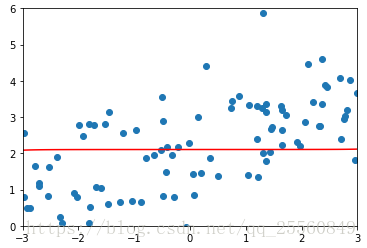
修改alpha值，分别为1,100,100000。可以看出线条逐渐变得平滑，当alpha很大的时候，为了使目标函数小，所以会使系数趋近于0，因此会得出几乎平行的一条直线。

3.LASSO正则化

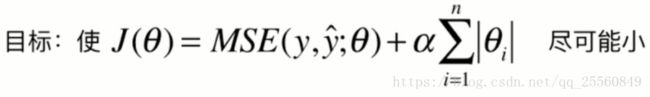
lasso的全拼为：least absolute shrinkage and selection operator regression。

4.lasso代码实现

from sklearn.linear_model import Lasso
def RridgeRegression(degree,alpha):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),
        ("std_scaler",StandardScaler()),
        ("lin_reg",Lasso(alpha=alpha))    
    ])
ridge1 = RridgeRegression(20,0.1)
ridge1.fit(x_train,y_train)
y_test = ridge1.predict(x_test)
#mean_squared_error(y_test,x_test)
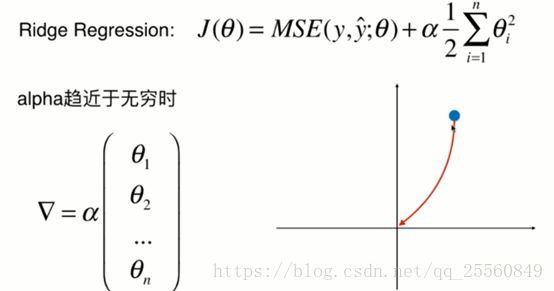
plot_model(ridge1)

绘制出的图像可以看出lasso回归拟合的图像更趋近于直线。lasso会趋向于使得一部分θ值变为0，所以可以作为特征选取，这就是selection operator的含义。下面简单介绍下其中的原因。

如图上图所示，对于岭回归，在求解目标函数最小值时，假设alpha趋近无穷，初始系数点为蓝色点，将会沿着红线趋于0，在这个过程中θ都是有值的。

而对于lasso回归，因为θ不可导，只能写成如上图所示的分段函数。

七、L1,L2和弹性网络

1.比较岭回归和lasso回归

这里回归下明科夫斯基距离。

  

将上面式子进行泛化，表达成如下形式，得出了L1,L2正则项，分别对应lasso和岭回归（只是没有进行开方，但是也称为L2）。

实际上还存在L0正则项，即希望θ尽可能少，一般很少使用。

2.弹性网

弹性网的意义比较简单，即将岭回归和lasso回归一起考虑，结合两个项的优点，通过r来调整两个项的比例。