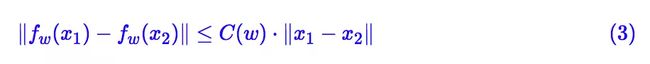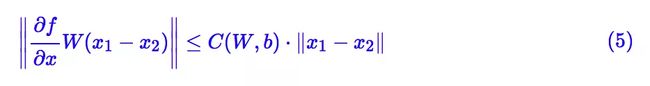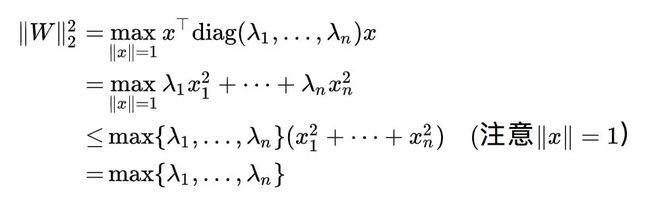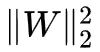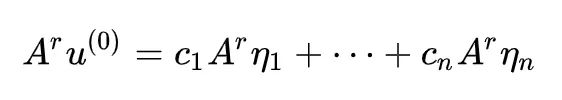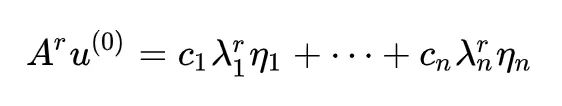Lipschitz定义、连续性、以及深度学习中如何使用、为何使用？特征值迭代计算
本文总结关于Lipschitz的定义与应用，并且给出相关链接，如有侵权，立即删除。
建议各位读者点解原文查看更多更清晰的内容~
1. Lipschitz定义
参考文章： https://blog.csdn.net/yzxnuaa/article/details/79725736
2. Lipschitz常数
参考文章：https://blog.csdn.net/Chaolei3/article/details/81202544
3. 深度学习中的Lipschitz约束：泛化与生成模型
参考文章：https://www.jiqizhixin.com/articles/2018-10-16-19
L约束与泛化
扰动敏感
记输入为 x，输出为 y，模型为 f，模型参数为 w，记为：
很多时候，我们希望得到一个“稳健”的模型。何为稳健？一般来说有两种含义，一是对于参数扰动的稳定性，比如模型变成了 fw+Δw(x) 后是否还能达到相近的效果？如果在动力学系统中，还要考虑模型最终是否能恢复到 fw(x)；二是对于输入扰动的稳定性，比如输入从 x 变成了 x+Δx 后，fw(x+Δx) 是否能给出相近的预测结果。
读者或许已经听说过深度学习模型存在“对抗攻击样本”，比如图片只改变一个像素就给出完全不一样的分类结果，这就是模型对输入过于敏感的案例。
L约束
所以，大多数时候我们都希望模型对输入扰动是不敏感的，这通常能提高模型的泛化性能。也就是说，我们希望 ||x1−x2|| 很小时：
也尽可能地小。当然，“尽可能”究竟是怎样，谁也说不准。于是 Lipschitz 提出了一个更具体的约束，那就是存在某个常数 C（它只与参数有关，与输入无关），使得下式恒成立
也就是说，希望整个模型被一个线性函数“控制”住。这便是 L 约束了。
换言之，在这里我们认为满足 L 约束的模型才是一个好模型。并且对于具体的模型，我们希望估算出 C(w) 的表达式，并且希望 C(w) 越小越好，越小意味着它对输入扰动越不敏感，泛化性越好。
神经网络
在这里我们对具体的神经网络进行分析，以观察神经网络在什么时候会满足 L 约束。
简单而言，我们考虑单层的全连接 f(Wx+b)，这里的 f 是激活函数，而 W,b 则是参数矩阵/向量，这时候 (3) 变为：
让 x1,x2 充分接近，那么就可以将左边用一阶项近似，得到：
显然，要希望左边不超过右边，∂f/∂x 这一项（每个元素）的绝对值必须不超过某个常数。这就要求我们要使用“导数有上下界”的激活函数，不过我们目前常用的激活函数，比如sigmoid、tanh、relu等，都满足这个条件。假定激活函数的梯度已经有界，尤其是我们常用的 relu 激活函数来说这个界还是 1，因此 ∂f/∂x 这一项只带来一个常数，我们暂时忽略它，剩下来我们只需要考虑 ||W(x1−x2)||。
多层的神经网络可以逐步递归分析，从而最终还是单层的神经网络问题，而 CNN、RNN 等结构本质上还是特殊的全连接，所以照样可以用全连接的结果。因此，对于神经网络来说，问题变成了：如果下式恒成立，那么 C 的值可以是多少？
找出 C 的表达式后，我们就可以希望 C 尽可能小，从而给参数带来一个正则化项。
矩阵范数
定义
其实到这里，我们已经将问题转化为了一个矩阵范数问题（矩阵范数的作用相当于向量的模长），它定义为：
如果 W 是一个方阵，那么该范数又称为“谱范数”、“谱半径”等，在本文中就算它不是方阵我们也叫它“谱范数（Spectral Norm）”好了。注意 ||Wx|| 和 ||x|| 都是指向量的范数，就是普通的向量模长。而左边的矩阵的范数我们本来没有明确定义的，但通过右边的向量模型的极限定义出来的，所以这类矩阵范数称为“由向量范数诱导出来的矩阵范数”。
好了，文绉绉的概念就不多说了，有了向量范数的概念之后，我们就有：
呃，其实也没做啥，就换了个记号而已，||W||2 等于多少我们还是没有搞出来。
Frobenius范数
其实谱范数 ||W||2 的准确概念和计算方法还是要用到比较多的线性代数的概念，我们暂时不研究它，而是先研究一个更加简单的范数：Frobenius 范数，简称 F 范数。
这名字让人看着慌，其实定义特别简单，它就是：
说白了，它就是直接把矩阵当成一个向量，然后求向量的欧氏模长。
简单通过柯西不等式，我们就能证明：
很明显 ||W||F 提供了 ||W||2 的一个上界，也就是说，你可以理解为 ||W||2 是式 (6) 中最准确的 C（所有满足式 (6) 的 C 中最小的那个），但如果你不大关心精准度，你直接可以取 C=||W||F，也能使得 (6) 成立，毕竟 ||W||F 容易计算。
l2正则项
前面已经说过，为了使神经网络尽可能好地满足L约束，我们应当希望 C=||W||2 尽可能小，我们可以把 C2 作为一个正则项加入到损失函数中。当然，我们还没有算出谱范数 ||W||2，但我们算出了一个更大的上界 ||W||F，那就先用着它吧，即 loss 为：
其中第一部分是指模型原来的 loss。我们再来回顾一下 ||W||F 的表达式，我们发现加入的正则项是：
这不就是 l2 正则化吗？
终于，捣鼓了一番，我们得到了一点回报：我们揭示了 l2 正则化（也称为 weight decay）与 L 约束的联系，表明 l2 正则化能使得模型更好地满足 L 约束，从而降低模型对输入扰动的敏感性，增强模型的泛化性能。
谱范数
主特征根
这部分我们来正式面对谱范数 ||W||2，这是线性代数的内容，比较理论化。
事实上，谱范数 ||W||2 等于
的最大特征根（主特征根）的平方根，如果 W是方阵，那么||W||2 等于 W 的最大的特征根绝对值。
对于感兴趣理论证明的读者，这里提供一下证明的大概思路。根据定义 (7) 我们有：
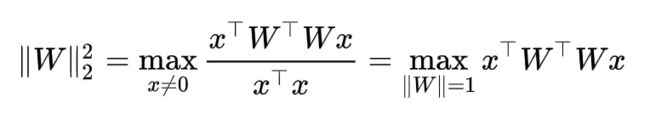假设
对角化为diag(λ1,…,λn)，即
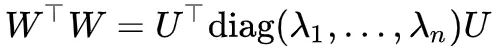，其中 λi 都是它的特征根，而且非负，而 U 是正交矩阵，由于正交矩阵与单位向量的积还是单位向量，那么：
所以
等于
的最大特征根。
幂迭代
也许有读者开始不耐烦了：鬼愿意知道你是不是等于特征根呀，我关心的是怎么算这个鬼范数！
事实上，前面的内容虽然看起来茫然，但却是求 ‖W‖2 的基础。前一节告诉我们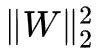
就是
的最大特征根，所以问题变成了求
的最大特征根，这可以通过“幂迭代”法 [3] 来解决。
所谓“幂迭代”，就是通过下面的迭代格式：
迭代若干次后，最后通过：
得到范数（也就是得到最大的特征根的近似值）。也可以等价改写为：
这样，初始化 u,v 后（可以用全 1 向量初始化），就可以迭代若干次得到 u,v，然后代入
算得 ‖W‖2 的近似值。
对证明感兴趣的读者，这里照样提供一个简单的证明表明为什么这样的迭代会有效。
记，初始化为
，同样假设 A 可对角化，并且假设 A 的各个特征根 λ1,…,λn 中，最大的特征根严格大于其余的特征根（不满足这个条件意味着最大的特征根是重根，讨论起来有点复杂，需要请读者查找专业证明，这里仅仅抛砖引玉。
当然，从数值计算的角度，几乎没有两个人是完全相等的，因此可以认为重根的情况在实验中不会出现。），那么 A 的各个特征向量 η1,…,ηn 构成完备的基底，所以我们可以设：
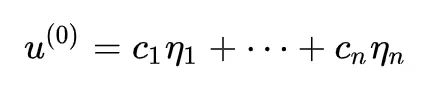每次的迭代是 Au/‖Au‖，其中分母只改变模长，我们留到最后再执行，只看 A 的重复作用：
注意对于特征向量有 Aη=λη，从而：
不失一般性设 λ1 为最大的特征值，那么：
根据假设 λ2/λ1,…,λn/λ1 都小于 1，所以 r→∞ 时它们都趋于零，或者说当 r 足够大时它们可以忽略，那么就有：
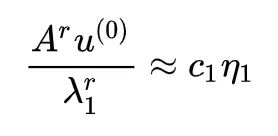先不管模长，这个结果表明当 r 足够大时，
提供了最大的特征根对应的特征向量的近似方向，其实每一步的归一化只是为了防止溢出而已。这样一来
就是对应的单位特征向量，即：
因此：
，这就求出了谱范数的平方。
谱正则化
前面我们已经表明了 Frobenius 范数与 l2 正则化的关系，而我们已经说明了 Frobenius 范数是一个更强（更粗糙）的条件，更准确的范数应该是谱范数。虽然谱范数没有 Frobenius 范数那么容易计算，但依然可以通过式 (15) 迭代几步来做近似。
所以，我们可以提出“谱正则化（Spectral Norm Regularization）”的概念，即把谱范数的平方作为额外的正则项，取代简单的 l2 正则项。即式 (11) 变为：
Spectral Norm Regularization for Improving the Generalizability of Deep Learning [1]一文已经做了多个实验，表明“谱正则化”在多个任务上都能提升模型性能。
在 Keras 中，可以通过下述代码计算谱范数：
def spectral_norm(w, r=5):
w_shape = K.int_shape(w)
in_dim = np.prod(w_shape[:-1]).astype(int)
out_dim = w_shape[-1]
w = K.reshape(w, (in_dim, out_dim))
u = K.ones((1, in_dim))
for i in range(r):
v = K.l2_normalize(K.dot(u, w))
u = K.l2_normalize(K.dot(v, K.transpose(w)))
return K.sum(K.dot(K.dot(u, w), K.transpose(v)))