2019年Byte Camp夏令营5月25日笔试题解

笔试题共有4题编程题，前3题较为简单，本文给出相应的思路和解答。

第1题

题目大意：给出n个景点，每个景点有相应的分值$a_1,a_2,...,a_n$。小明一天之内要游玩两个景点$i,j$，景点之间的距离为下标之差的绝对值$|i-j|$，满意度为景点的分值之和减去景点之间的距离，公式为$a_i+a_j+i-j,(j>i)$。要求为小明选出两个景点，给出最大的满意度。
输入：共两行。第一行为n，表示有n个景点；第二行按序给出每个景点的分值。
输出：输出最大的满意度。

解题思路：本题很简单，使用两个for循环即可，但是时间复杂度为$O(n^2)$。本人就使用此方法解题，但是由于时间复杂度太高，只通过了60%的测试用例。大致代码如下：

    public class Solution {
        ...
        public static int handler(int[] arr) {
            int max = 0;
            for (int i = 0; i < arr.length; ++i) {
                for (int j = i + 1; j < arr.length; ++j) {
                    int temp = arr[i] + arr[j] + i - j;
                    max = max >= temp ? max : temp;
                }
            }
            return max;
        }
    }

  后来尝试使用$O(nlogn)$的时间复杂度，但是没有想到合适的办法。在笔试结束后，突然对有了领悟：$a_i+a_j+i-j=(a_i+i)+(a_j-j),(j>i)$。细看此式，有点类似于求一个数组中两个数的最大和，因此$O(n)$的复杂度即可解决此问题：

import java.util.Scanner;

public class Solution {
    
    punlic static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = sc.nextInt();
        }
        System.out.println(handler(arr));
    }
    
    public static int handler(int[] arr) {
        if (arr == null || arr.length == 0) return 0;
        
        // maxI保存当前arr[i]+i最大的值
        int maxI = arr[0];
        // max保存当前最大的满意度，即arr[i]+i+arr[j]-j最大
        int max = 0;
        for (int i = 1; i < arr.length; ++i) {
            max = max >= maxI + arr[i] - i ? max : maxI + arr[i] - i;
            maxI = maxI >= arr[i] + i ? max : arr[i] + i;
        }
        return max;
    }
}

---

第2题

题目大意:给出一个二维数组，数组中元素的值为1或0。要求找出数组中的块数，每一块由任意个相连的1组成，相连规则：当前元素为1，且其上、下、左、右、左上、左下、右上、右下，只要这8个位置任意一个位置中元素为1，则当前元素与此元素相连。
输入：第一行为m、n，m代表数组行数，n代表数组列数。此后为m*n行，代表要二维数组。
输出：数组中的块数。

示例：
输入：
3 3
0 1 0
1 0 0
1 0 1
输出：2（右下角的1独自成一块，其余三个1相连成一块）

解题思路：扫描二维数组，每次遇到值为1的元素，就对其所在的块进行处理。处理过程，将当前元素置0，并判断其相邻的8个位置是否为1，如果为1则对其进行相同处理，如果为0则不处理。

import java.util.Scanner;
public class Solution {
    pulic static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int m = sc.nextInt();
        int n = sc.nmextInt();
        int[] arr = new int[m][n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j)
                arr[i][j] = sc.nextInt();
        }
        
        int num = findBlockNum(arr);
        System.out.println(num);
    }
    
    public static int findBlockNum(int[][] arr) {
        if (arr == null || arr.length == 0) return 0;
        
        int m = arr.length;
        int n = arr[0].length;
        
        // 保存块数
        int num = 0;
    
        // 遍历数组中的每一个元素
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (arr[i][j] == 1) {
                    // 将整个块找出来
                    exploreBlock(arr, i, j);
                    ++num;
                }
            }
        }
        return num;
    }
    
    public static void exploreBlock(int[][] arr, int i, int j) {
        if (arr == null || arr.length == 0) return;
        
        // 边界情况
        if (i >= arr.legnth || i < 0) return;
        if (j >= arr[0].length || j < 0) return;
        
        // 先将当前位置的1置0
        // 置0的好处：
        // 1. 当对其相邻为1的元素进行同样处理时，不会再次处理当前位置，
        // 避免陷入循环调用，造成栈溢出
        // 2. 当前位置置0，避免findBlock函数中的循环再次对元素进行处理
        arr[i][j] = 0;
        explore(arr, i-1, j-1);
        explore(arr, i-1, j);
        explore(arr, i-1, j+1);
        explore(arr, i, j-1);
        explore(arr, i, j+1);
        explore(arr, i+1, j-1);
        explore(arr, i+1, j);
        explore(arr, i+1, j+1);
        
        return;
    }
}

  上述代码在运行时只通过了80%的测试用例。据说是因为使用太多递归调用，在处理较大的数组时，导致栈溢出。因此，可以将递归调用改成while循环和列表。

import java.util.Scanner;
import java.util.ArrayList;

pulic class Solutin {
    public class Point {
        public int i, j;
        public Point(int i, int j) {
            this.i = i;
            this.j = j;
        }
    }
    
    // main等函数和上面一样，此处省略
    ...
    
    public static void exploreBlock(int[][] arr, int i, int j) {
        List<Point> list = new ArrayList<Point>;
        list.add(new Point(i, j));
        Point tempP;
        while (list.size() > 0) {
            tempP = list.get(0);
            list.remove(0);
            arr[tempP.i][tempP.j] = 0;
            checkPoint(arr, tempP.i-1, tempP.j-1, list);
            checkPoint(arr, tempP.i-1, tempP.j, list);
            checkPoint(arr, tempP.i-1, tempP.j+1, list);
            checkPoint(arr, tempP.i, tempP.j-1, list);
            checkPoint(arr, tempP.i, tempP.j+1, list);
            checkPoint(arr, tempP.i+1, tempP.j-1, list);
            checkPoint(arr, tempP.i+1, tempP.j, list);
            checkPoint(arr, tempP.i+1, tempP.j+1, list);
        }
        
        return;
    }
    
    public static void checkPoint(int[][] arr, int i, int j, List<Point> list) {
        if (arr == null || arr.length == 0) return;
        
        // 边界情况
        if (i >= arr.legnth || i < 0) return;
        if (j >= arr[0].length || j < 0) return;
        
        if (arr[i][j] == 1) list.add(new Point(i, j));
        return;
    }
}

---

第3题

题目大意：给出一个字符串，要求将%到#之间的字符串复制n次，n为%之前的数字。%#可嵌套。
输入：一行字符串
输出：处理后的字符串

示例：
输入：2%g3%n##
输出：gnnngnnn

解题思路：对于%#可嵌套的问题可用栈进行解决。先入栈的后处理，后入栈的先处理。至于如何识别数字、符号%和#以及要复制的字符串，可用自动机来处理。

图1
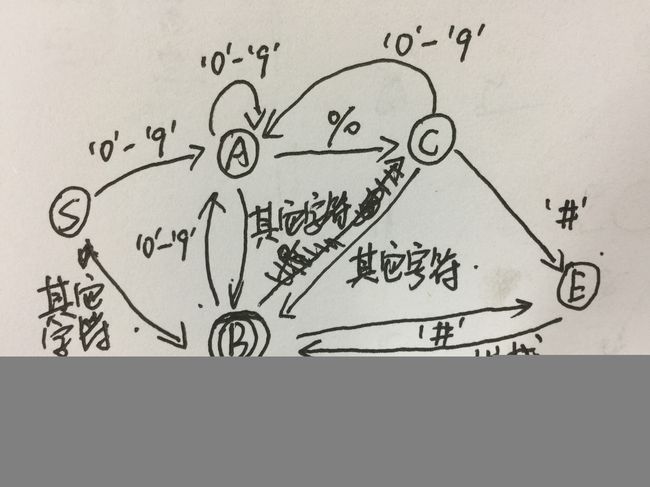
  维护一个全局变量string，表示最终的字符串。
  对于上图，从起始状态S开始，依次读取字符串中的字符。如果当前字符是’0’-‘9’，则转到状态A，状态A对数字进行处理；如果是其它字符，则转为状态B，状态B对字符串进行拼接。
  状态A维护一个字符串tempA，拼接数字字符。从A出发，如果当前字符是’0’-‘9’,则状态A继续接收，如果是’%’，则表明这是一个复制操作，如果当前栈中所保存的’%‘不为0，则表明这同时是一个嵌套的复制操作，将tempC压入栈中，并将tempC置空，转到状态C，同时并将tempA压入栈中，将当前栈中所保存的操作个数+1，表示要复制的操作嵌套的个数；如果是其它字符，则表明此前读取的数字都是普通字符串，不代表复制的倍数，转到状态B，并将tempA清空。
  对于状态C，如果当前字符为’#’，则表示’%‘到’#‘之间的字符串个数为0，压入一个空字符串进栈，转到状态E；如果当前字符是其它字符，则维护一个字符串tempC，转到状态B。
  对于状态E，如果当前栈中所保存的操作个数不为0，则从栈中弹出两个元素，依次为：要复制的元素、复制的次数。将字符串复制之后给tempE，如果当前栈中所保存的操作个数为0，即栈空，则将tempE保存到string中，否则弹出栈中的栈顶字符串，保存到tempC中，转到状态B。
  对于状态B，如果当前字符是’0’-‘9’，转到状态A；如果是其它字符，则判断当前栈中所保存的操作个数，如果不为0，则保存到tempC中，表明这个字符属于要复制的字符串，否则就将它保存到string中；如果当前字符是’#’，则判断当前栈中所保存的草走个数，如果为0，表示这不是一个复制操作的结尾，将其放入string中，否则将tempC压入栈中，转到状态E。

package testing;

import java.util.Scanner;
import java.util.Stack;

public class Solution {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String input = sc.nextLine();
        input = handler(input);
        System.out.println(input);
    }

    public static String handler(String s) {
        if (s == null || s.length() <= 3) return s;

        Stack<String> stack = new Stack<String>();
        String string = "", numStr = "", tempC = "";
        int operNum = 0;

        for (int i = 0; i < s.length(); ++i) {
            // 当前字符是数字
            if (s.charAt(i) > '0' && s.charAt(i) < '9') {
                // 当前栈中操作数不为零，则可能是嵌套，先将tempC压栈保存
                if (operNum > 0) {
                    stack.push(tempC);
                    tempC = "";
                }
                numStr += s.charAt(i);
            }
            else if (s.charAt(i) == '%') {
                // 判断numStr是否为空，如果不为空，则认为是复制操作
                if (!numStr.equals("")) {
                    stack.push(numStr);
                    numStr = "";
                    ++operNum;
                }
                // 否则，"%"只是普通字符 
                else {
                    if (operNum > 0)
                        tempC += "%";
                    else
                        string += "%";
                }
            }
            else if (s.charAt(i) == '#') {
                // 判断栈中操作数
                if (operNum > 0) {
                    // 将要复制的字符串tempC压入栈中
                    if (stack.size() % 2 == 0) {
                        tempC = stack.pop() + numStr + tempC;
                        numStr = "";
                    }
                    stack.push(tempC);
                    tempC = "";
                    String temp = copyString(stack);
                    --operNum;

                    // 如果操作数不为0，弹出栈中要复制的字符串
                    if (operNum > 0) {
                        tempC = stack.pop();
                        tempC += temp;
                    } else {
                        string += temp;
                    }
                } else {
                    string += numStr;
                    numStr = "";
                    string += "#";
                }
            }
            // 其他字符
            else {
                // 此处要处理状态A到状态B的情况
                // 即numStr中的数字只是普通字符
                if (operNum > 0) {
                    tempC += numStr;
                    tempC += s.charAt(i);
                }
                else {
                    string += numStr;
                    string += s.charAt(i);
                }
                numStr = "";
            }
        }

        return string;
    }

    public static String copyString(Stack<String> stack) {
        if (stack == null || stack.isEmpty()) return "";

        String s = stack.pop();
        int times = Integer.valueOf(stack.pop());
        String temp = s;

        while (times > 1) {
            s += temp;
            --times;
        }
        return s;
    }
}

上述代码测试用例通过率100%，但不能保证完全没问题。

以上几题题解供大家参考，欢迎大家指正！