囚徒困境、智猪博弈、纳什均衡与一致预期（博弈论入门学习笔记二）

0 囚徒困境：

        假定有两个犯罪嫌疑人共同作案。警察抓住他们以后，分开拘押，并告诉他们：可以选择坦白，或是不坦白；如果一个人坦白，而另一个人不坦白，则坦白的一方会被立即释放，而不坦白的一方被判10年；如果两人都坦白，则会每人各判8年；如果两人都抵赖，因证据不足，则每人在关押1年后释放。那么，这两个犯罪嫌疑人该如何选择呢？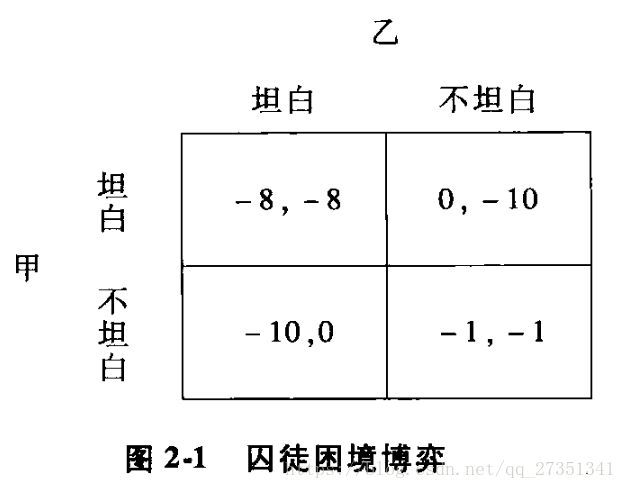

        现在我们来看参与人甲和乙会如何决策。我们假设参与人是理性的，都不想坐牢，能少坐牢尽量少坐牢。我们先考虑甲的选择，他面对的问题是：如果乙坦白的话，自己坦白判8年，不坦白判10年，那么坦白比不坦白好；如果乙不坦白，自己坦白会被立即释放，不坦白则判1年，坦白还是比不坦白好。因此，不论对方坦白不坦白，甲或乙自己的最优选择都是坦白。

占优均衡：一般来说，由于每个参与人的效用依赖于所有人的选择，因此每个人的最优选择（战略）也依赖于所有其他人的选择（战略）。但由囚徒困境我们可以看出，一个人的最优选择并不依赖于他人的选择。这样的最优战略，被称为“占优战略”。由所有参与人的占优战略构成的战略组合被称为“占优均衡”。
        占优战略均衡的出现只要求所有人都是理性的，但不要求每个参与人知道其他人是否理性。
        囚徒困境博弈有占优均衡，所以其结果很容易预测。
        “囚徒困境”表明个人理性与集体理性的冲突。这样的例子有很多：寡头竞争，军备竞赛，团队生产中的劳动供给，公共产品的供给，等等。许多的制度就是为了解决“囚徒困境”而存在的。

         私人产品是志愿购买的，但公共产品可能需要强制购买；税收制度就是保证公共产品的生产，解决公共产品生产上的“囚徒困境”。
囚徒困境的一般表示：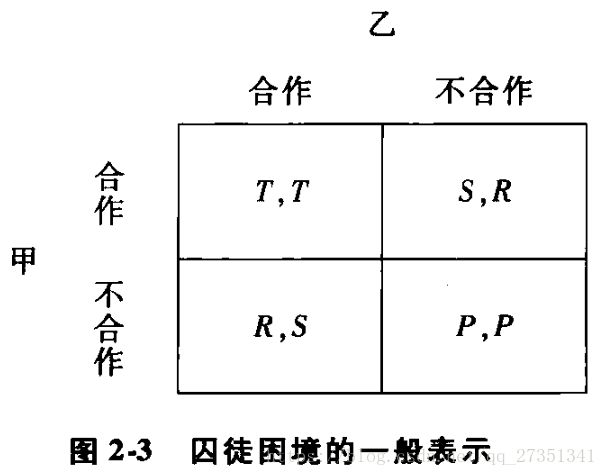

要使上述博弈成为一个囚徒困境需要满足这样一个条件：R>T>P>S。
解决囚徒困境的一种方式：用法律解决“囚徒困境”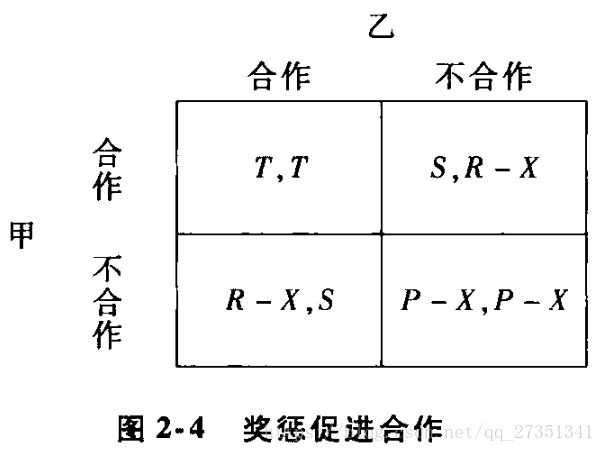

满足：X>R-T

1 “智猪博弈”：

设想猪圈里有两头猪，一头大猪和一头小猪。在猪圈的一头装有一个按钮，另一头装有食槽。在这头按下按钮，那头的食槽会有8单位的实物出现；于是出现如下博弈：

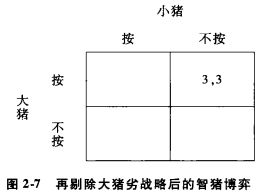
        有些博弈没有占优均衡，但通过剔除“坏”战略，我们可以预测博弈的结果。比如“智猪博弈”，在这个博弈中，大猪的最优选择依赖于小猪的选择，但小猪的最优选择与大猪的选择无关。如果大猪知道小猪是理性的，大猪将选择“按”。均衡是“大猪按，小猪等待”。

        “劣”战略：无论对方选择什么，如果自己选择A得到的收益总是小于选择B得到的收益，A就是相对于B的劣战略。

        重复剔除占优均衡：首先找出博弈参与人的劣战略（假定存在的话），把这个劣战略剔除后；然后再剔除剩下的新的博弈中的劣战略；继续这个过程，直到没有劣战略存在。如果剩下的战略组合是唯一的，这个唯一的战略组合就是“重复剔除占优均衡”。如果这样的解存在，我们说该博弈是“重复剔除占优可解的”。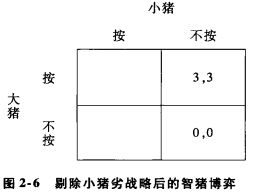

2 理性共识：

       0阶理性共识：每个人都是理性的，但不知道其他人是否是理性的；
       1阶理性共识：每个人是理性的，并且知道其他每个人也都是理性的，但并不知道其他人是否知道自己是理性的；
       2阶理性共识：每个人是理性的，并且知道其他每个人也都是理性的，并且知道其他人知道自己是理性的，但不知道其他人是否知道自己知道其他人都是理性的。。。。。。。三阶、四阶。。。n阶依次类推。
        重复剔除不仅要求每个人是理性的，而且要求每个人知道其他人都是理性的，每个人知道每个人知道每个人是理性的，如此等等，即理性是“共识”。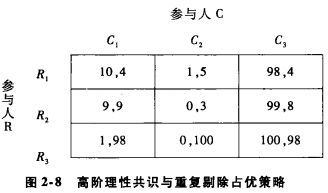

很多博弈没有占优均衡，也没有重复剔除的占优均衡。考虑如下博弈：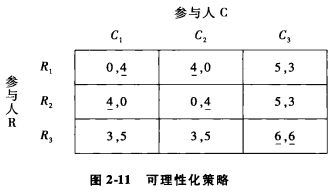

        相互一致性信念：要求每个参与人对别人的行为的预期都是正确的。

        内在一致性信念：参与人有合理的理由认为别人会做出何种选择。
        根据相互一致性预期，如果两个理性的人有相同的信息，那么他们就一定会得出相同的推断或相同的结论。（2005年诺贝尔经济学奖）。上述博弈有9个可能的战略组合，其中只有（R3,C3）满足一致预期（根据相互一致性信念，每个人对别人的行为的预期都是正确的）。

3 纳什均衡与一致预期：

        纳什均衡：所有参与人的最优战略的组合：给定该战略中别人的选择，没有人有积极性改变自己的选择。

        一致预期：基于信念的选择是合理的；支持选择的信念是正确的。

        预期的自我实现：如果所有人都认为这个结果会出现，这个结果就会出现。预期是自我实现的，预期不会错误。
        纳什均衡有一个很重要的特点，即信念和选择之间的一致性。就是说，基于信念的选择是合理的，同事支持这个选择的信念也是正确的。纳什均衡也可以说是可以自我实施的，也就是说，如果所有人都认为这个结果会出现，这个结果就真的会出现。
        如果参与人事前达成一个协议，在不存在外部强制的情况下，每个人都有积极性遵守这个协议，这个协议就是纳什均衡。
寻找纳什均衡：（R2，C2）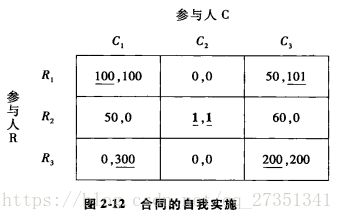

考虑如下囚徒困境：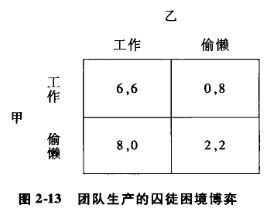

利用所有权解决囚徒困境：使其中一个人成为所有者，另一个人变成雇员，让前者监督后者。

4 混合策略下的纳什均衡：

考虑如下博弈：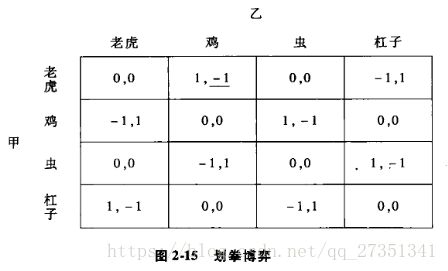

       这个博弈没有纳什均衡。现在我们引入另一个概念：混合战略纳什均衡，之前讲到的纳什均衡指的是纯战略纳什均衡，即确定地选择某一特定的战略，如果两个战略互为最优，就是一个（纯战略）纳什均衡。与纯战略相对应，混合战略是指，参与人以某一概率随机地选择某一行动。比如在划拳博弈中，每个参与者的最优选择一定是要随机地出招，从而使对方无法猜测到自己要出什么。
        现在我们来看一个混合战略纳什均衡的应用例子——监督博弈。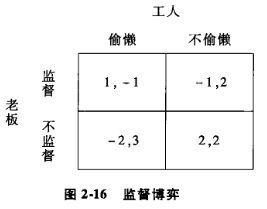

        在这个例子中，员工不偷懒、老板不监督是最好的（总收益最大），但这不是一个纳什均衡。如果员工不偷懒，则老板不监督；但如果员工知道老板不监督，员工则偷懒；如果老板知道员工偷懒，老板则监督。。。。形成一个循环。
        假如老板认为员工偷懒的概率是P，不偷懒的概率是1-P，从老板的角度看，监督的预期收益是：
                                              1×P+(-1)×(1-P)=2P-1。。。。（1）
        如果不监督，预期收益为：
                                              (-2)×P+2×(1-P)=1-4P。。。。（2）

        另（1）=（2），得P=1/3，这时，员工选择以1/3的概率偷懒，2/3的概率不偷懒，老板监督与不监督是一样的。

        假如老板以Q的概率选择监督，1-Q的概率选择不监督，这时，从员工的角度，选择偷懒的预期收益是：
                                              (-1)×Q+3×(1-Q)=3-4Q。。。。（3）
        选择不偷懒的预期收益为：
                                              2×Q+2×(1-Q)=2。。。。（4）
        要使员工的选择在这两者之间无差异，则另（3）=（4），得Q=1/4；意味着老板以1/4的概率监督，3/4的概率不监督。

        因此，混合战略纳什均衡是：员工以1/3的概率偷懒，2/3的概率不偷懒；老板以1/4的概率监督，3/4的概率不监督。

纳什均衡的存在性问题：（一般存在奇数个纳什均衡）
        1、每一个有限博弈至少存在一个纳什均衡（纯战略或混合战略）；
        2、如果一个博弈存在两个纯战略纳什均衡，那么，一定存在第三个混合战略纳什均衡。

5 高风险下的纳什均衡

        在一些特殊情况下，即使犯错误的可能性很小也可能导致大的灾难（比如核电站，出问题就非常严重），纳什均衡就可能不会产生有说服力的解释。考虑如下博弈：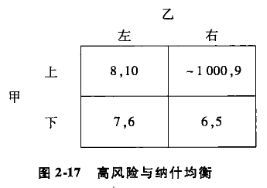

        在这个博弈中，参与人甲会选择“下”，因为如果乙不小心（低概率）犯错误，要避免产生右上的灾难性情况。
        这个例子说明，个体可能不想我们所假设的那样完全理性，在遇到高风险的情况下，人们会考虑风险，从而使得最终结果可能偏离纳什均衡战略。